Open App

Class 7 Exam > Class 7 Notes > Mathematics (Maths) Class 7 > NCERT Solutions: Comparing Quantities

NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Exercise 7.1

Q1: Convert the given fractional numbers to percent:
(a) 1/8
(b) 5/4
(c) 3/40
(d) 2/7
Ans: To convert the given fraction into percent we multiply the fraction by 100 and put the percent (%) Sign :

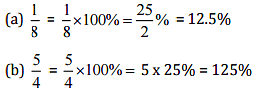
Q2: Convert the given decimal fractions to per cents:
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Ans: To convert the decimals into percent, first convert them into fraction and then multiply by 100 and put percent sign.
(a) 0.65:
0.65 can be written as 65/100.
To convert it to a percentage, we multiply it by 100.
(65/100) * 100 = 65%
Therefore, 0.65 is equal to 65%.

(b) 2.1:
2.1 remains the same.
To convert it to a percentage, we multiply it by 100.
2.1 * 100 = 210%
Therefore, 2.1 is equal to 210%.

(c) 0.02:
0.02 can be written as 2/100.
To convert it to a percentage, we multiply it by 100.
(2/100) * 100 = 2%
Therefore, 0.02 is equal to 2%.

(d) 12.35:
12.35 remains the same.
To convert it to a percentage, we multiply it by 100.
12.35 * 100 = 1235%
Therefore, 12.35 is equal to 1235%.

Q3: Estimate what part of the figures is coloured and hence find the percent which is coloured.

NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Ans: (i) We can observe that only 1 part is coloured out of 4 parts.
Therefore, Coloured part = 1/4
∴ Percent of coloured part = 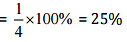NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(ii) We can observe that only 3 parts is coloured out of 5 parts.
Therefore, Coloured part = 3/5
∴ Percent of coloured part 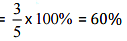NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(iii) We can observe that only 3 parts is coloured out of 8 parts.
Therefore, Coloured part = 3/8
∴ Percent of coloured part NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
= 37.5%

Q4: Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of 2500
(d) 75% of 1 kg
Ans:
(a) 15% of 250 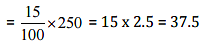NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(b) We know that, 1 hour = 60 minutes = 60 x 60 seconds = 3600 seconds
1% of 1 hours = 1% of 60 minutes = 1% of (60 x 60] second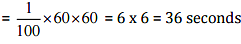
NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(c) 20% of Rs 2500 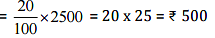NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(d) 75% of 1 kg = 75% of 1000 g 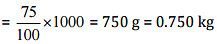NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Q5: Find the whole quantity if:
(a) 5% of it is 600
(b) 12% of it is ₹1080
(c) 40% of it is 500 km
(d) 70% of it is 14 minutes
(e) 8% of it is 40 litres
Ans: Let the whole quantity be x in given questions:

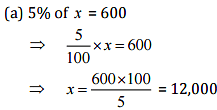
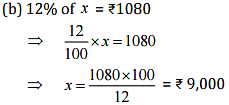
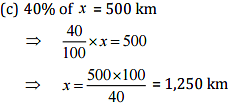
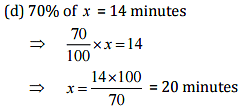
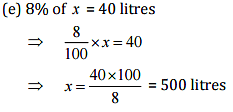
NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Q6: Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Ans:

S. No.	Per cents	Fractions	Simplest form	Decimal form
(a)	25%	25/100	1/4	0.25
(b)	150%	150/100	3/2	1.5
(c)	20%	20/100	1/5	0.2
(d)	5%	5/100	1/20	0.05

Q7: In a city, 30% are females, 40% are males and remaining are children. What percent are children?
Ans:
Given:
Percentage of females = 30%
Percentage of males = 40%
Total percentage of females and males = 30 + 40 = 70%
Percentage of children = Total percentage - Percentage of males and females
= 100% - 70%
= 30%
Hence, 30% are children.

Q8: Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Ans: Total voters = 15,000
Percentage of voted candidates = 60%
Percentage of not voted candidates = 100 - 60 = 40%
Actual candidates, who did not vote = 40% of 15000 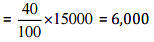NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
Hence, 6,000 candidates did not vote.

Q9: Meeta saves Rs 4000 from her salary. If this is 10% of her salary. What is her salary?
Ans: Let Meera's total salary be Rs x.
Now, 10% of salary = Rs 4000
⇒ 10% of x = Rs 400
⇒ (10/100) * x = Rs 4000
⇒ x = (4000 * 100)/10 = Rs 40,000
Hence, Meera's salary is Rs 40,000.

Q10: A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Ans: Number of matches played by cricket team = 20
Percentage of won matches = 25%
Total matches won by them = 25% of 20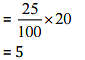
NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
Hence, they won 5 matches.

Exercise 7.2

Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.

(a) Gardening shears bought for ₹250 and sold for ₹325.

Profit/Loss: ₹325 - ₹250 = ₹75 (Profit)
Profit per cent: $\frac{75}{250} \times 100 = 30 %$

(b) A refrigerator bought for ₹12,000 and sold at ₹13,500.

Profit/Loss: ₹13,500 - ₹12,000 = ₹1,500 (Profit)
Profit per cent: $\frac{1500}{12000} \times 100 = 12.5\%$

Profit/Loss: ₹3,000 - ₹2,500 = ₹500 (Profit)
Profit per cent: $\frac{500}{2500} \times 100 = 20\%$

(d) A skirt bought for ₹250 and sold at ₹150.

Profit/Loss: ₹150 - ₹250 = -₹100 (Loss)
Loss per cent: $\frac{100}{250} \times 100 = 40\%$

2. Convert each part of the ratio to percentage:

(a) 3 : 1

Total parts = 3 + 1 = 4
Percentage of first part: $\frac{3}{4} \times 100 = 75\$
Percentage of second part: $\frac{1}{4} \times 100 = 25\%$ 41×100=25%

(b) 2 : 3 : 5

Total parts = 2 + 3 + 5 = 10
Percentage of first part: $\frac{2}{10} \times 100 = 20\%$ 102×100=20%
Percentage of second part: $\frac{3}{10} \times 100 = 30\%$
Percentage of third part: $\frac{5}{10} \times 100 = 50\%$

Total parts = 1 + 4 = 5
Percentage of first part: $\frac{1}{5} \times 100 = 20\%$
Percentage of second part: $\frac{4}{5} \times 100 = 80\%$

(d) 1 : 2 : 5

Total parts = 1 + 2 + 5 = 8
Percentage of first part: $\frac{1}{8} \times 100 = 12.5\%$
Percentage of second part: $\frac{2}{8} \times 100 = 25\%$
Percentage of third part: $\frac{5}{8} \times 100 = 62.5\%$

3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.

Decrease in population: 25,000 - 24,500 = 500
Percentage decrease: $\frac{500}{25000} \times 100 = 2\%$

4. Arun bought a car for ₹3,50,000. The next year, the price went up to ₹3,70,000. What was the Percentage of price increase?

Increase in price: ₹3,70,000 - ₹3,50,000 = ₹20,000
Percentage increase: $\frac{20000}{350000} \times 100 = 5.71\%$

5. I buy a T.V. for ₹10,000 and sell it at a profit of 20%. How much money do I get for it?

Profit: 20% of ₹10,000 = $\frac{20}{100} \times 10000 = ₹2000$
Selling price: ₹10,000 + ₹2,000 = ₹12,000

6. Juhi sells a washing machine for ₹13,500. She loses 20% in the bargain. What was the price at which she bought it?

Loss: 20% of Cost Price (CP)
Selling Price (SP) = ₹13,500
Therefore, SP = CP - 20% of CP
$\text{₹13,500} = CP - \frac{20}{100} \times CP$
$₹13,500 = CP \times (1 - 0.20)$
$₹13,500 = 0.80 \times CP$
$C P = \frac{₹}{13} = ₹ 16, 875$

7. (i) Chalk contains calcium, carbon and oxygen in the ratio 10:3:12. Find the percentage of carbon in chalk.

Total parts = 10 + 3 + 12 = 25
Percentage of carbon: $\frac{3}{25} \times 100 = 12 %$

(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?

Carbon percentage: 12%
Therefore, $12 %$ of weight of chalk = 3g
Let the weight of chalk be $W$
$\frac{12}{100} \times W = 3$
$W = \frac{3}{\times} = 25 g$

8. Amina buys a book for ₹275 and sells it at a loss of 15%. How much does she sell it for?

Loss: 15% of ₹275 = $\frac{15}{100} \times 275 = ₹41.25$
Selling price: ₹275 - ₹41.25 = ₹233.75

9. Find the amount to be paid at the end of 3 years in each case:

(a) Principal = ₹1,200 at 12% p.a.

Simple Interest: $\frac{1200 \times 12 \times 3}{100} =$
Amount: ₹1,200 + ₹432 = ₹1,632

(b) Principal = ₹7,500 at 5% p.a.

Simple Interest: $\frac{7500 \times 5 \times 3}{100} = ₹1,125$
Amount: ₹7,500 + ₹1,125 = ₹8,625

10. What rate gives ₹280 as interest on a sum of ₹56,000 in 2 years?

Interest (I): ₹280
Principal (P): ₹56,000
Time (T): 2 years
Using the formula for Simple Interest: $I = \frac{P \times R \times T}{100}$
$\frac{280}{\times} = R$
$R = \frac{28000}{112000} = 0.25\%$

If Meena gives an interest of ₹45 for one year at 9% rate p.a., what is the sum she has borrowed?

Interest (I): ₹45

Rate (R): 9%

Time (T): 1 year

Using the formula for Simple Interest: $I = \frac{P \times R \times T}{100}$

$\frac{45 \times 100}{9 \times 1} = P$

$P = 500$

Deleted Exercise

Q1: Find the ratio of:
(a) Rs5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hours

Ans: To find ratios, both quantities should be in same unit.
(a) Rs 5 to 50 paise
⇒ 5 x 100 paise to 50 paise [∴ Rs 1 = 100 paise]
⇒ 500 paise to 50 paise
Thus, the ratio is = 500/50 = 10/1 = 10 : 1

(b) 15 kg to 210 g
⇒ 15 x 1000 g to 210 g [∵ 1kg = 1000 g]
⇒ 15000 g to 210 g
Thus, the ratio is = 15000/210 = 500/7 = 500:7

(d) 30 days to 36 hours
⇒ 30 x 24 hours to 36 hours [∵ 1 day = 24 hours]
⇒ 720 hours to 36 hours
Thus, the ratio is = 720/36 = 20/1 = 20:1

Q2: In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Ans:
∵ 6 students need = 3 computers
∵ 1 student needs = 3/6 computers
Therefore, 24 students need = 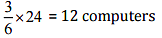NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
Thus, 12 computers will be needed for 24 students.

Q3: Population of Rajasthan = 570 lakhs and population of U.P. = 1660 lakhs. Area of Rajasthan = 3 lakh km2 and area of U.P. = 2 lakh km2.
(i) How many people are there per km2 in both states?
(ii) Which state is less populated?
Ans:

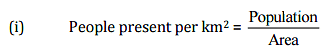
NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

(ii) By comparing the above two states we can clearly observe that Rajasthan is less populated.

The document NCERT Solutions for Class 7 Maths - Comparing Quantities- 1 is a part of the Class 7 Course Mathematics (Maths) Class 7.

All you need of Class 7 at this link: Class 7

	Mathematics (Maths) Class 7 76 videos\|345 docs\|39 tests

Mathematics (Maths) Class 7

76 videos|345 docs|39 tests

Join Course for Free

Top Courses for Class 7

View all

FAQs on NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

1. How can I compare quantities using ratios and proportions?

Ans. To compare quantities using ratios and proportions, you can set up a ratio of the two quantities and simplify it to its simplest form. This will allow you to easily compare the two quantities and determine their relationship.

2. What is the difference between direct and inverse proportions when comparing quantities?

Ans. In direct proportion, as one quantity increases, the other quantity also increases at the same rate. Inverse proportion, on the other hand, is when one quantity increases while the other decreases at a proportional rate.

3. How can I calculate the percentage increase or decrease when comparing quantities?

Ans. To calculate the percentage increase or decrease when comparing quantities, you can use the formula: Percentage Change = (New Value - Old Value) / Old Value x 100%. This will give you the percentage difference between the two quantities.

4. Can I compare quantities using fractions instead of ratios?

Ans. Yes, you can compare quantities using fractions as well. Simply convert the quantities into fractions and compare them by finding a common denominator or simplifying the fractions to their simplest form.

5. What are some real-life examples where comparing quantities is important?

Ans. Real-life examples where comparing quantities is important include comparing prices at different stores to find the best deal, comparing the nutritional content of different foods, and comparing the performance of different investments to make informed decisions.

Related Exams

Grade 7

About this Document

	25.7K Views
	4.95/5 Rating
	Nov 15, 2024 Last updated

Document Description: NCERT Solutions: Comparing Quantities for Class 7 2024 is part of Mathematics (Maths) Class 7 preparation. The notes and questions for NCERT Solutions: Comparing Quantities have been prepared according to the Class 7 exam syllabus. Information about NCERT Solutions: Comparing Quantities covers topics like Exercise 7.1, Exercise 7.2, Deleted Exercise and NCERT Solutions: Comparing Quantities Example, for Class 7 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions: Comparing Quantities.

Introduction of NCERT Solutions: Comparing Quantities in English is available as part of our Mathematics (Maths) Class 7 for Class 7 & NCERT Solutions: Comparing Quantities in Hindi for Mathematics (Maths) Class 7 course. Download more important topics related with notes, lectures and mock test series for Class 7 Exam by signing up for free. Class 7: NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Description

Full syllabus notes, lecture & questions for NCERT Solutions for Class 7 Maths - Comparing Quantities- 1 - Class 7 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 7 | Best notes, free PDF download

Information about NCERT Solutions: Comparing Quantities

In this doc you can find the meaning of NCERT Solutions: Comparing Quantities defined & explained in the simplest way possible. Besides explaining types of NCERT Solutions: Comparing Quantities theory, EduRev gives you an ample number of questions to practice NCERT Solutions: Comparing Quantities tests, examples and also practice Class 7 tests

	Mathematics (Maths) Class 7 76 videos\|345 docs\|39 tests

Mathematics (Maths) Class 7

76 videos|345 docs|39 tests

Join Course for Free

Download as PDF

Explore Courses for Class 7 exam

Top Courses for Class 7

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

shortcuts and tricks

past year papers

Objective type Questions

Previous Year Questions with Solutions

MCQs

Semester Notes

NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Free

practice quizzes

ppt

Viva Questions

mock tests for examination

pdf

Extra Questions

video lectures

Sample Paper

study material

Summary

NCERT Solutions for Class 7 Maths - Comparing Quantities- 1

Exam

Important questions

;

Additional Information about NCERT Solutions: Comparing Quantities for Class 7 Preparation

NCERT Solutions: Comparing Quantities Free PDF Download

The NCERT Solutions: Comparing Quantities is an invaluable resource that delves deep into the core of the Class 7 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the NCERT Solutions: Comparing Quantities now and kickstart your journey towards success in the Class 7 exam.

Importance of NCERT Solutions: Comparing Quantities

The importance of NCERT Solutions: Comparing Quantities cannot be overstated, especially for Class 7 aspirants. This document holds the key to success in the Class 7 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

NCERT Solutions: Comparing Quantities Notes

NCERT Solutions: Comparing Quantities Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to NCERT Solutions: Comparing Quantities. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions: Comparing Quantities Notes on EduRev are your ultimate resource for success.

NCERT Solutions: Comparing Quantities Class 7 Questions

The "NCERT Solutions: Comparing Quantities Class 7 Questions" guide is a valuable resource for all aspiring students preparing for the Class 7 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study NCERT Solutions: Comparing Quantities on the App

Students of Class 7 can study NCERT Solutions: Comparing Quantities alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the NCERT Solutions: Comparing Quantities, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of NCERT Solutions: Comparing Quantities is prepared as per the latest Class 7 syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup