NCERT Solutions for Class 8 Maths - Algebraic Expressions- 2
Exercise 10.2
Q1: If m = 2, find the value of:
(i) m - 2
(ii) 3m - 5
(iii) 9 - 5m
(iv) 3m2 - 2m - 7
(v) 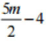
Sol:
(i) m - 2 = 2 - 2 [Putting m = 2]
= 0
(ii) 3m - 5 = 3 x 2 - 5 [Putting m = 2]
= 6 - 5 = 1
(iii) 9 - 5m = 9 - 5 x 2 [Putting m = 2]
= 9 - 10 = - 1
(iv) 3m2 - 2m - 7
= 3(2)2 - 2 (2) - 7 [Putting m = 2]
= 3 x 4 - 2 x 2 - 7
= 12-4-7
= 12- 11 = 1
(v) 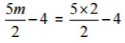 [Putting m = 2]
[Putting m = 2]
= 5 - 4 = 1
Q2: If p = -2, find the value of:
(i) 4p + 7
(ii) - 3p2 + 4p + 7
(iii) -2p3 - 3p2 +4/7 + 7
Sol:
(i) 4p + 7 = 4 (- 2) + 7 [Putting p= -2]
= -8 + 7 = -1
(ii) -3p2+4p + 7
= -3 (-2)2+ 4 (-2) + 7 [Putting p = - 2]
= - 3 x 4 - 8 + 7
= - 12 - 8 + 7
= -20 + 7 = -13
(iii) - 2p3 - 3p2 +4p + 7
= - 2 (-2)3 - 3(-2)2 + 4 (-2) + 7 [Putting p = - 2]
= -2 x(-8)-3 x4 -8 + 7
= 16-12-8 + 7
= -20 + 23 = 3
Q3: Find the value of the following expressions, when x = -1:
(i) 2x - 7
(ii) -x + 2
(iii) x2 + 2x + 1
(iv) 2x2- x - 2
Sol:
(i) 2x - 7 = 2 (-1) - 7 [Putting x= - 1]
= - 2 - 7 = - 9
(ii) - x + 2 = - (-1) + 2 [Putting x= - 1]
= 1 + 2 = 3
(iii) x2 + 2 x + 1 = (-1)2 + 2 (-1) + 1 [Putting x= - 1]
= 1 - 2 + 1
= 2 - 2 = 0
(iv) 2x2- x - 2 = 2 (-1)2 - (-1) - 2 [Putting x= - 1]
= 2x1 + 1-2
= 2 + 1 - 2
= 3 - 2 = 1
Q4: If a = 2,b = -2, find the value of:
(i) a2 + b2
(ii) a2+ab + b2
(iii) a2 - b2
Sol:
(i) a2 + b2 ( 2)2 + (- 2)2 [Putting a = 2. b = - 2 ]
= 4 + 4 = 8
(ii) a2+ab + b2
= (2) + ( 2) (- 2) +(-2)2 [Putting a = 2. b = - 2 ]
= 4 - 4 + 4 = 4
(iii) a2 - b2 = (2)2 - (-2)2 [Putting a = 2,b = - 2]
= 4 - 4 = 0
Q5: When a = 0, b = -1, find the value of the given expressions:
(i) 2a + 2b
(ii) 2a2+b2+1
(iii) 2a2b + 2ab2 +ab
(iv) a2+ab+2
Sol:
(i) 2a + 2b = 2 (0) + 2 (-1) [Putting a - 0,b = - 1]
= 0 - 2 = -2
(ii) 2a2 + b2 + 1 = 2 (0)2 + (-1)2 + 1 [Putting a - 0,b = - 1]
= 2 x 0 + 1+ 1 = 0 + 2 = 2
(iii) 2a2b + 2ab2 + ab = 2(0)2 (-1) + 2 (0 )(-1)2 + (0 )(-1) [Putting a - 0,b = - 1]
= 0 + 0 + 0 = 0
(iv) a2 +ab + 2 - (0)2 + (0) (-1) + 2 [Putting a - 0,b = - 1]
= 0 + 0 + 2 = 2
Q6: Simplify the expressions and find the value if x is equal to 2:
(i) x + 7 + 4 (x- 5)
(ii) 3 (x + 2) + 5x - 7
(iii) 6x + 5 (x - 2)
(iv) 4 (2x - 1) + 3x + 11
Sol:
(i) x + 7 + 4(x- 5) = x + 7 + 4x - 20 = x + 4 x + 7 - 20
= 5 x - 13 = 5 x 2 - 13 [Putting x = 2]
= 10-13 = -3
(ii) 3 (x+ 2) + 5x - 7 = 3x + 6 + 5x -7 = 3x + 5x + 6 - 7
= 8x - 1 = 8 x 2-1 [Putting x = -1]
= 16 - 1 = 15
(iii) 6x + 5 (x - 2) = 6x + 5x -10 = 11x - 10
= 11 x 2 - 10 [Putting x = -1]
= 22 - 10 = 12
(iv) 4(2x - 1) + 3x + 11 = 8x - 4 + 3x +11 = 8x + 3a - 4 + 11
= 11a + 7 = 11 x 2 + 7 [Putting x = - 1]
= 22+7 = 29
Q7: Simplify these expressions and find their values if x = 3,a = -1, b = - 2 :
(i) 3x - 5 - x + 9
(ii) 2 - 8x + 4x + 4
(iii) 3a + 5 - 8a + 1
(iv) 10 - 3b - 4 - 5b
(v) 2a - 2b - 4 - 5 + a
Sol:
(i) 3a - 5 - x + 9 = 3x - x - 5 + 9 = 2x + 4
= 2x3+4 [Putting a = 3]
= 6 + 4 = 10
(ii) 2 - 8x + 4x + 4 = - 8x + 4x + 2 + 4 = -4x + 6
= - 4 x 3 + 6 [Putting a = 3]
= -12 + 6 =12
(iii) 3a + 5 - 8a + 1 = 3a - 8a + 5 + 1 = - 5a + 6
= -5(- 1) + 6 [Putting a = - 1]
= 5 + 6 = 11
(iv) 10 - 3b - 4 - 5b = - 3b - 5b + 10 - 4 = -8b+6
= -8 (-2)+ 6 [Putting b = -2]
= 16 + 6 = 22
(v) 2a - 2b - 4 - 5 + a = 2a + a - 2b - 4 - 5
= 3a - 2b - 9 = 3 (-1)-2 (-2) -9 [Putting a = -1 , b = - 2]
= -3 + 4 -9 = -8
Q8:
(i) If z = 10, find the value of z3 - 3 (z - 10).
(ii) If p = - 10, find the value of p2 - 2p - 100
Sol:
(i) z3 -3(z-10) = (10)3-3(10 - 10) [Putting z = 10]
= 1000 - 3 x 0 = 1000- 0
= 1000
(ii) p2 - 2p - 100 = (-10)2 - 2 (-10) - 100 (Putting p = - 10]
= 100+ 20 - 100 = 20
Q9: What should be the value of a if the value of 2x2 + x - a equals to 5, when x = 0 ?
Sol:
Given: 2x2 + x - a = 5
⇒ 2 (0)2 + 0 - a = 5 [Putting x = 0]
⇒ 0 + 0 - a = 5
⇒ a = -5
Hence, the value of a is -5.
Q10: Simplify the expression and find its value when a = 5 and b = - 3: 2 (a2 + ab) + 3 - ab
Sol:
Given: 2 (a2 + ab) + 3 - ab
⇒ 2a2 + 2ab + 3 - ab
⇒ 2a2 + 2ab - ab + 3
⇒ 2a2 + ab + 3
⇒ 2 (5)2 + (5) (-3) + 3 [Putting a = 5 , b = -3]
⇒ 2 x 25 - 15 + 3
⇒ 50 - 15 + 3
⇒ 38
FAQs on NCERT Solutions for Class 8 Maths - Algebraic Expressions- 2
| 1. What are algebraic expressions? |  |
| 2. How do you simplify algebraic expressions? |  |
| 3. What are the different types of algebraic expressions? |  |
| 4. How can we evaluate algebraic expressions? |  |
| 5. What are the applications of algebraic expressions? |  |

|
Explore Courses for Class 7 exam
|

|


















