Patterns in Mathematics NCERT Solutions | Mathematics for Class 6 PDF Download
| Table of contents |

|
| Page 2 |

|
| Page 3 |

|
| Page 4 & 5 |

|
| Page 6 |

|
| Page 7 |

|
| Page 8 & 9 |

|
| Page 10 & 11 |

|
| Page 12 |

|
Page 2
Figure it Out
Q1. Can you think of other examples where mathematics helps us in our everyday lives?
Ans: Here are a few examples of where mathematics helps us in our everyday lives:
- Managing money (budgeting, expenses)
- Cooking (measurements, proportions)
- Shopping (discounts, totals)
- Home improvement (measuring, areas)
- Travel (distances, time, expenses)
- Fitness (calories, BMI)
- Time management (schedules)
- Gardening (spacing, layouts)
These examples show how mathematics is a practical tool for solving everyday problems and making informed decisions.
Q2. How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses, or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Ans: Mathematics has been important in moving humanity forward in many ways:
- Science (experiments, natural laws)
- Economy & Democracy (financial models, election analysis)
- Engineering (safe buildings, bridges)
- Technology (computers, phones, algorithms)
- Transport (design, speed, fuel, navigation)
- Timekeeping (clocks, calendars)
- Medicine (dosages, imaging, disease modeling)
- Space (planet paths, space missions)
Page 3
Table 1: Examples of number sequences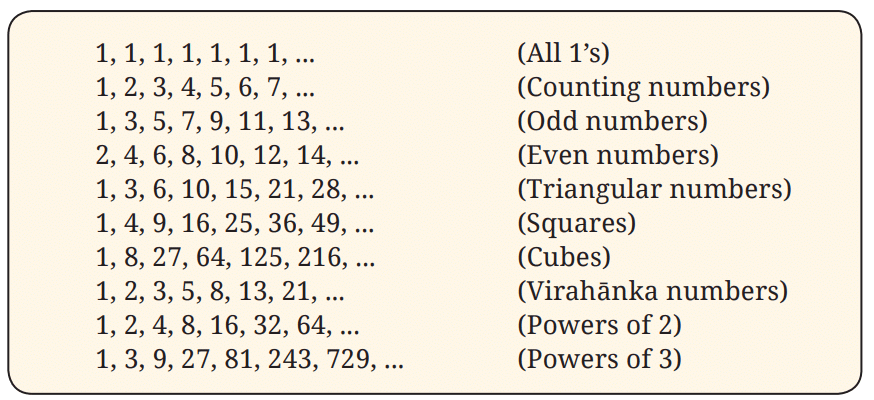
Figure it Out
Q1. Can you recognize the pattern in each of the sequences in Table 1?
Ans: (a) 1, 1, 1, 1, 1, 1, 1,……
The number ‘1’ is repeated.
(b) 1, 2, 3, 4, 5, 6, 7,……
Counting numbers starting from ‘1’.
Start from 1. Keep adding 1.
(c) 1, 3, 5, 7, 9, 11, 13,…..
Odd numbers starting from ‘1’.
Start from 1. Keep adding 2.
(d) 2, 4, 6, 8, 10, 12, 14,…..
Even numbers starting from ‘2’.
Start from 2. Keep adding 2.
(e) 1, 3, 6, 10, 15, 21, 28,…..
Triangular numbers
Start from 1. Add 2: 1 + 2 = 3
Then add 3: 3 + 3 = 6
Then add 4: 6 + 4 = 10 and so on.
(f) 1, 4, 9, 16, 25, 36, 49,…..
Squares (number multiplied by itself) of counting numbers.
1st number = 1 × 1 = 1
2nd number = 2 × 2 = 4
3rd number = 3 × 3 = 9
4th number = 4 × 4 = 16 and so on.
(g) 1, 8, 27, 64, 125, 216,……
Cubes (number multiplied by itself and again with itself) of counting numbers.
1st number = 1 × 1 × 1 = 1
2nd number = 2 × 2 × 2 = 8
3rd number = 3 × 3 × 3 = 27
4th number = 4 × 4 × 4 = 64 and so on.
(h) 1, 2, 3, 5, 8, 13, 21,……
Virahanka numbers (Sum of last 2 numbers)
1st number = 1, 2nd number = 2
3rd number = 2nd number + 1st number = 2 + 1 = 3
4th number = 3rd number + 2nd number = 3 + 2 = 5
5th number = 4th number + 3rd number = 5 + 3 = 8
6th number = 5th number + 4th number = 8 + 5 = 13 and so on.
Starting from the 3rd every number is the sum of two previous numbers.
(i) 1, 2, 4, 8, 16, 32, 64,……
Powers of 2
20 = 1
21 = 2
22 = 2 × 2 = 4
23 = 2 × 2 × 2 = 8 and so on.
(j) 1, 3, 9, 27, 81, 243, 729,……
Powers of 3
30 = 1
31 = 3
32 = 3 × 3 = 9
33 = 3 × 3 × 3 = 27 and so on.
Q2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Ans: (a) 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,……….. (repeat 1 three times)
(b) 1, 2, 3, 4, 5, 6, 7, 8, 9,10,…….. (next three counting numbers)
(c) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,……….. (next three odd numbers)
(d) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,……….. (next three even numbers)
(e) 1, 3, 6, 10, 15, 21, 28, 36, 45, 55,………. (next three triangular numbers)
28 + 8 = 36
36 + 9 = 45
45 + 10 = 55
(f) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,………. (next three squares)
8 × 8 = 64
9 × 9 = 81
10 × 10 = 100
(g) 1, 8, 27, 64, 125, 216, 343, 512, 729,………. (next three cubes)
7 × 7 × 7 = 343
8 × 8 × 8 = 512
9 × 9 × 9 = 729
(h) 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…………. (next Virahanka numbers)
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
(i) 1, 2, 4, 8, 16, 32, 64, 128, 256, 512,……….. (multiply the previous number by 2)
64 × 2 = 128
128 × 2 = 256
256 × 2 = 512
(j) 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683,………. (multiply the previous number by 3)
729 × 3 = 2187
2187 × 3 = 6561
6561 × 3 = 19683
Page 4 & 5
Table 2 Pictorial representation of some number sequences 
Figure it Out
Q1. Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!
Ans: 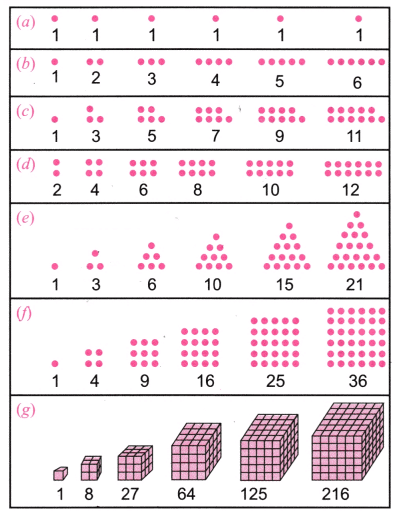
Q2.
(a) Why are 1, 3, 6, 10, 15,…… called triangular numbers?
(b) Why are 1, 4, 9, 16, 25,…….. called square numbers or squares?
(c) Why are 1, 8, 27, 64, 125,…….. called cubes?
Ans: (a) Triangular numbers are called so because these numbers of dots can be arranged to make a triangle. 1, 3, 6, 10,…….. are triangular numbers. 1, 3, 6, 10,……… dots can be arranged to make a triangle. (see figure below)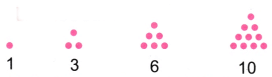 (b) Square numbers are called so because these numbers of dots can be arranged to make a square.
(b) Square numbers are called so because these numbers of dots can be arranged to make a square.
1, 4, 9, 16,………. are square numbers.
1, 4, 9, 16,……… dots can be arranged to make a square (see fig. below)
(c) Cubes are called so because these many unit cubes can be arranged to make a cube.
1, 8, 27, 64,…… are cube numbers.
1, 8, 27, 64,……. unit cubes can be arranged to make cubes. (see figure below)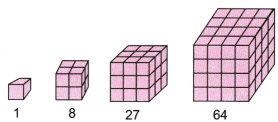
Q3. You will have noticed that 36 is a triangular and square number! That is, 36 dots can be arranged perfectly both in a triangle and a square. Make pictures in your notebook illustrating this! This shows that the same number can be represented differently, and play different roles) depending on the context. Try representing some other numbers pictorially in different ways!
Ans: Three other such numbers are 1, 1225, and 41616.
1225 is the 49th triangular number.
Also, 1225 can be represented by a square having 36 dots along its side.
Q4. What would you call the following sequence of numbers?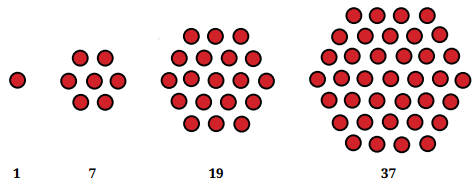
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Ans: 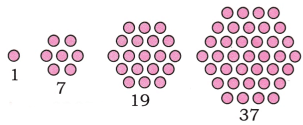
1st number = 1
2nd number = 1 + 6 = 7 (2nd number = 1st number + 6 × 1)
3rd number = 7 + 12 = 19 (3rd number = 2nd number + 6 × 2)
4th number = 19 + 18 = 37 (4th number = 3rd number + 6 × 3)
5th number = 37 + 24 = 61 (5th number = 4th number + 6 × 4)
Hence, the next number in the sequence is 61.
Q5. Can you think of pictorial ways to visualize the sequence of Powers of 2? Powers of 3? Here is one possible way of thinking about Powers of 2: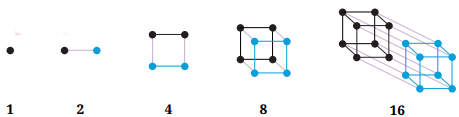 Ans: Pictorial Representation for powers of 3: 1, 3, 9, 27
Ans: Pictorial Representation for powers of 3: 1, 3, 9, 27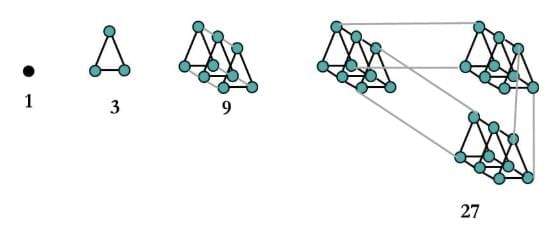
Page 6
Example: What happens when we start adding up odd numbers?
1 = 1 = square of 1
1 + 3 = 4 = square of 2
1 + 3 + 5 = 9 = square of 3
1 + 3 + 5 + 7 = 16 = square of 4
1 + 3 + 5 + 7 + 9 = 25 = square of 5
1 + 3 + 5 + 7 + 9 + 11 = 36 = square of 6
Why does this happen? Do you think it will happen forever?
Ans: This happens because each odd number can be represented as (2n – 1), where (n) is a positive integer. When we sum the first (n) odd numbers, we get: 1 + 3 + 5 + ……. + (2n – 1) = n
This pattern will continue forever because it is a fundamental property of numbers. The sequence of odd numbers and their sums forming perfect squares is an inherent characteristic of the number system.
How can we partition the dots in a square grid into odd numbers of dots: 1, 3, 5, 7,…..?
Ans: We can partition the dots in a square grid into odd numbers of dots: 1, 3, 5, 7, as follows:
Page 7
By drawing a similar picture, can you say what is the sum of the first 10 odd numbers?
Ans: Sum of first 10 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = n2 = (10)2 = 10 × 10 = 100
Now by imagining a similar picture, or by drawing it partially, as needed, can you say what is the sum of the first 100 odd numbers?
Ans: The sum of the first 100 odd numbers = 1 + 3 + 5 + …………
= n2
= (100)2
= 100 × 100
= 10,000
Page 8 & 9
Q1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1,……., gives square numbers?
Ans: 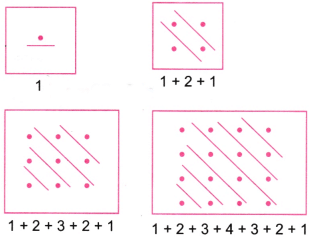
1 = 1 = (1)2
1 + 2 + 1 = 4 = (2)2
1 + 2 + 3 + 2 + 1 = 9 = (3)2
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 = (4)2
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 = (5)2
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36 = (6)2 and so on.
Q2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1 + 2 + 3+……+99 + 100 + 99+…….+ 3 + 2 + 1?
Ans: 1 + 2 + 3 + …… + 100 + ……. + 3 + 2 + 1 = 100 × 100 = 10000
Hence, it is 1002 = 100 × 100 = 10,000
Q3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?
Ans: Adding up: 1 + 1 + 1 + 1 = 4
Adding down: 1 + 1 + 1 + 1 = 4
The sum is the same in both ways.
Q4. Which sequence do you get when you start to add the Counting numbers up? Can you give a smaller pictorial explanation?
Ans: 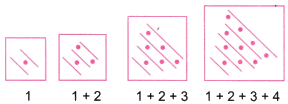 Counting numbers adding up:
Counting numbers adding up:
1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4,
Or 1, 3, 6, 10
Q5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15,……..? Which sequence do you get? Why? Can you explain it with a picture?
Ans: 1 + 3 = 4 = 2 × 2;
3 + 6 = 9 = 3 × 3;
6 + 10 = 16 = 4 × 4
The above pairs give square numbers.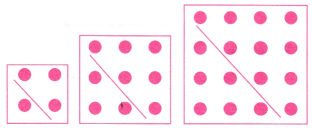
Q6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8,…..? Now add 1 to each of these numbers — what numbers do you get? Why does this happen?
Ans: Let us add powers of 2 starting with 1
Here 1 = 1
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
1 + 2 + 4 + 8 + 16 = 31
Hence series 1, 3, 7, 15, 31,….. is formed.
Now let us add 1 to each of the above numbers
1 + 1 = 2 = 21
1 + 2 + 1 = 4 = 2 × 2 = 22
1 + 2 + 4 + 1 = 8 = 2 × 2 × 2 = 23
1 + 2 + 4 + 8 + 1 = 16 = 2 × 2 × 2 × 2 = 24
This happens because we are adding (1 + 1 = 2), hence the power of 2 increases.
Q7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Ans: Triangular numbers are 1, 3, 6, 10, 15, 21,…….
1 × 6 + 1 = 7
3 × 6 + 1 = 19 (increase of 12 i.e. 6 × 2)
6 × 6 + 1 = 37 (increase of 18 i.e. 6 × 3)
10 × 6 + 1 = 61 (increase of 24 i.e. 6 × 4)
15 × 6 + 1 = 91 (increase of 30 i.e. 6 × 5)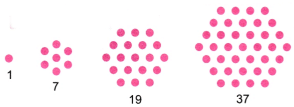 We get the sequence: 7, 19, 37, 61, 91,………..
We get the sequence: 7, 19, 37, 61, 91,………..
Q8. What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37,……? Which sequence do you get? Can you explain it using a picture of a cube?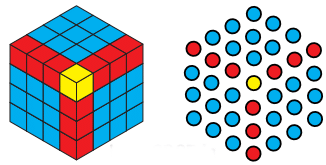
Ans: Hexagonal No. are: 1, 7, 19, 37,……….
Let us add them:
1 = 13 (third power of 1)
1 + 7 = 8 = 2 × 2 × 2 = 23 (third power of 2)
1 + 7 + 19 = 27 = 3 × 3 × 3 = 33 (third power of 3)
1 + 7 + 19 + 37 = 64 = 4 × 4 × 4 = 43 (third power of 4)
1 + 7 + 19 + 37 + 61 = 125 = 5 × 5 × 5 = 53 (third power of 5)
Q9. Find your own patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?
Ans: 3, 6, 9, 12, 15, 18,……… (consecutive multiples of 3).
10, 15, 20, 25,…….. (first number is 10. Then an increase of 5 in each term)
Page 10 & 11
Table 3 Examples of shape sequences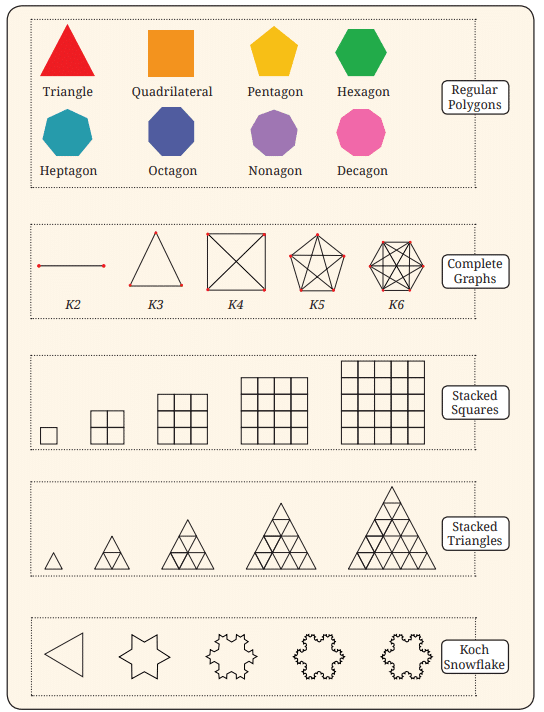 Q1. Can you recognize the pattern in each of the sequences in Table 3?
Q1. Can you recognize the pattern in each of the sequences in Table 3?
Ans: (a) Regular Polygons: Triangle, quadrilateral, pentagon, hexagon, (the number of sides increases by 1 at a time). Hence, it is a continuous number sequence starting from 3.
(b) Complete Graphs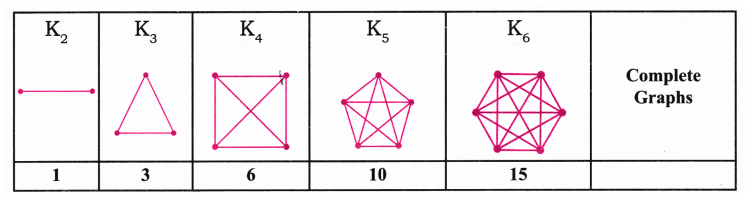
Here number of lines is as follows:
K2 = 1
K3 = 3
K4 = 6
K5 = 10
K6 = 15
The series formed is 1, 3, 6, 10, 15,…….
Hence it is a triangular number sequence.
(c) Stacked Squares: The number of small squares in each: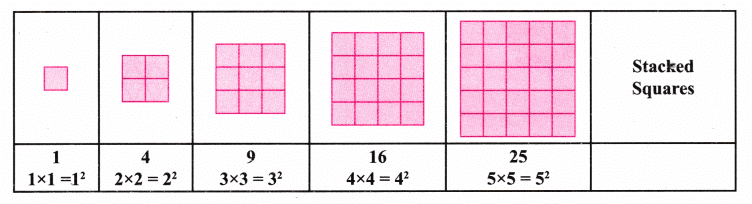
The series formed is 1, 4, 9, 16, 25,…….
Hence, it is a presentation of a square numbers sequence.
(d) Stacked Triangles: The number of small triangles in each: Hence it is also a square number sequence shown by triangles.
Hence it is also a square number sequence shown by triangles.
(e) Koch Snowflake: Number of sides in each becomes 4 times.
Q2. Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Ans: (a) Regular Polygon: A Polygon of 11 sides. (hendecagon)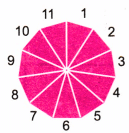 (b) K7
(b) K7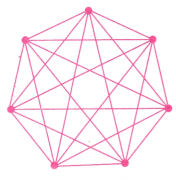 (c) Stacked Squares
(c) Stacked Squares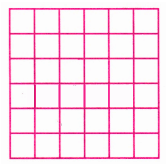
Total number of squares = 6 × 6 = 36
(d) Stacked Triangles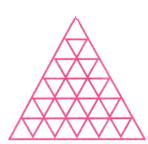 Total number of triangles = 1 + 3 + 5 + 7 + 9 + 11 = 36
Total number of triangles = 1 + 3 + 5 + 7 + 9 + 11 = 36
(e) Koch Snowflake
Figure it Out
Q1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Ans:  Both sequences s are the same because in a regular polygon number of sides is equal to several vertices.
Both sequences s are the same because in a regular polygon number of sides is equal to several vertices.
Q2. Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?
Ans:  Hence, we get the sequence: 1, 3, 6, 10, 15,…… It is a triangular number sequence.
Hence, we get the sequence: 1, 3, 6, 10, 15,…… It is a triangular number sequence.
Page 12
Q3. How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Ans: 
We get the sequence: 1, 4, 9, 16, 25, 36,……….
Hence, we get the sequence of square numbers.
Q4. How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why? (Hint: In each shape in the sequence, how many triangles are there in each row?)
Ans:  We get the sequence: 1, 4, 9, 16, 25, 36, 49, This is the sequence of square numbers.
We get the sequence: 1, 4, 9, 16, 25, 36, 49, This is the sequence of square numbers.
Hence by adding a Stacked Triangle at the bottom, the next number in the square sequence will come.
Q5. To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’ by a ‘speed bump’ __ⴷ__. As one does this more and more times, the changes become tinier and tinier with very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, ..., i.e., 3 times Powers of 4; this sequence is not shown in Table 1.)
Ans:  The sequence 3, 12, 48, 192, 768, and so on begins with 3.
The sequence 3, 12, 48, 192, 768, and so on begins with 3.
Each subsequent term is found by multiplying the previous term by 4.
Similarly, in the next Koch Snowflake iteration, four new lines are added for each line of the previous shape.
|
48 videos|334 docs|23 tests
|
FAQs on Patterns in Mathematics NCERT Solutions - Mathematics for Class 6
| 1. How can patterns in mathematics help students improve their problem-solving skills? |  |
| 2. What are some real-life applications of patterns in mathematics? |  |
| 3. How can students develop their pattern recognition skills in mathematics? |  |
| 4. Why is it important for students to understand patterns in mathematics? |  |
| 5. How can teachers incorporate pattern-based activities in their mathematics curriculum? |  |





















