NCERT Solutions for Class 8 Maths - Perimeter and Area- 2
Exercise 9.2
Q1: Find the circumference of the circles with the following radius:
(a) 14 cm
(b) 28 mm
(c) 21 cm
Sol:
(a) A circumference of the circle 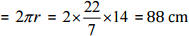
(b) A circumference of the circle 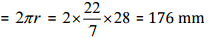
(c) A circumference of the circle 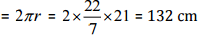
Q2: Find the area of the following circles, given that:
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm
Sol:
Q3: If the circumference of a circular sheet is 154 m, find its radius. Also, find the area of the sheet.
Sol:
Circumference of the circular sheet = 154 m
⇒ 2πr = 154 m
⇒ r = 154/2π
⇒ 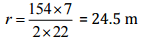
Now, Area of circular sheet =πr2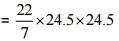
= 22 x 3.5 x 24.5 = 1886.5 m2
Thus, the radius and area of circular sheet are 24.5 m and 1886.5 m2 respectively.
Q4: A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase if he makes 2 rounds of a fence. Also, find the costs of the rope, if it cost Rs 4 per meter.
Sol:
Diameter of the circular garden = 21 m
∴ Radius of the circular garden = 21/2 m
Now, Circumference of a circular garden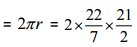
= 22 x 3 = 66 m
The gardener makes 2 rounds of a fence so the total length of the rope of fencing
= 2 x 2πr
= 2 x 66 = 132 m
Since, the cost of 1 meter rope = Rs 4
Therefore, Cost of 132 meter rope = 4 x 132 = Rs 528
Q5: From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet.
Sol:
Radius of circular sheet (R) = 4 cm and radius of removed circle (r) = 3 cm
Area of the remaining sheet = Area of a circular sheet - Area of removed circle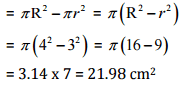
Thus, the area of the remaining sheet is 21.98 cm2.
Q6: Saima wants to put lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs 15.
Sol:
Diameter of the circular table cover = 1.5 m
∴ Radius of the circular table cover = 1.5/2 m
Circumference of circular table cover = 2πr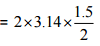 = 4.71 m
= 4.71 m
Therefore, the length of required lace is 4.71 m.
Now the cost of 1 m lace = Rs 15
Then the cost of 4.71 m lace = 15 x 4.71 = Rs 70.65
Hence, the cost of 4.71 m lace is Rs 70.65.
Q7: Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
Sol:
Diameter = 10 cm
Radius = 10/2 = 5 cm
According to question,
Perimeter of figure = Circumference of semicircle + diameter
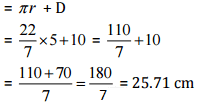
Thus, the perimeter of the given figure is 25.71 cm.
Q8: Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is Rs 15/m2. (Take π = 3.14)
Sol:
Diameter of the circular table top = 1.6 m
Radius of the circular table top = 1.6/2 = 0.8 m
Area of circular table top = πr2 = 3.14 x 0.8 x 0.8 = 2.0096 m2
Now, the cost of polishing 1 m2 = Rs 15
Then cost of polishing 2.0096 m2 = 15 x 2.0096 = Rs 30.14 (approx.)
Thus, The cost of polishing a circular table top is Rs 30.14 (approx.)
Q9: Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also, find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square?
Sol:
Total length of the wire = 44 cm
∴ The circumference of the circle = 2πr = 44 cm
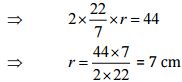
Now Area of the circle = πr2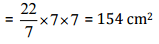
Now the wire is converted into the square.
The perimeter of square = 44 cm
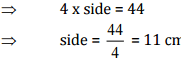
Now, area of square = side x side = 11 x 11 = 121 cm2
Therefore, on comparing, the area of the circle is greater than that of a square, so the circle encloses more area.
Q10: From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed (as shown in the adjoining figure). Find the area of the remaining sheet.
Sol:
Radius of circular sheet (R) = 14 cm and Radius of smaller circle (r) = 3.5 cm
Length of rectangle (l) = 3 cm and breadth of rectangle (b) = 1 cm
According to question,
Area of remaining sheet = Area of circular sheet- (Area of two smaller circle + Area of rectangle)
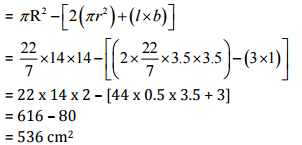
Therefore, the area of the remaining sheet is 536 cm2.
Q11: A circle of radius 2 cm is cut out from a square piece of an aluminum sheet of side 6 cm. What is the area of the leftover aluminum sheet?
Sol:
Radius of circle = 2 cm and side of aluminium square sheet = 6 cm
According to question,
Area of aluminum sheet left = Total area of aluminum sheet - Area of circle
= side x side - πr2
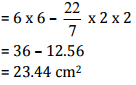
Therefore, the area of the aluminum sheet left is 23.44 cm2.
Q12: The circumference of a circle is 31.4 cm. Find the radius and the area of the circle.
Sol:
The circumference of the circle = 31.4 cm
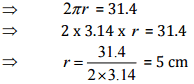
Then area of the circle = πr2 = 3.14 x 5 x 5
= 78.5 cm2
Therefore, the radius and the area of the circle are 5 cm and 78.5 cm2 respectively.
Q13: A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path?
Sol:
Diameter of the circular flower bed = 66 m
∴ Radius of circular flower bed (r) = 66/2 = 33 m
∴ Radius of circular flower bed with 4 m wide path (R) = 33 + 4 = 37 m
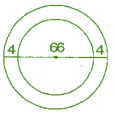
According to question,
Area of path = Area of bigger circle - Area of smaller circle
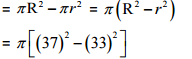
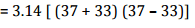
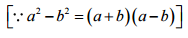
= 3.14 x 70 x 4
= 879.20 m2
Therefore, the area of the path is 879.20 m2.
Q14: A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden?
Sol:
Circular area covered by the sprinkler = πr2
= 3.14 x 12 x 12
= 3.14 x 144
= 452.16 m2
Area of the circular flower garden = 314 m2
As Area of the circular flower garden is smaller than area with a sprinkler. Therefore, the sprinkler will water the entire garden.
Q15: Find the circumference of the inner and the outer circles, shown in the adjoining figure.
Sol:
Radius of outer circle (r) = 19 m
Circumference of outer circle = 2πr = 2 x 3.14 x 19 = 119.32 m
Now radius of inner circle (r') = 19 - 10 = 9 m
∴ Circumference of inner circle = 2πr' = 2 x 3.14 x 9 = 56.52 m
Therefore, the circumferences of inner and outer circles are 56.52 m and 119.32 m respectively.
Q16: How many times a wheel of radius 28 cm must rotate to go 352 m?
Sol:
Let wheel must be rotated n times of its circumference.
Radius of wheel = 28 cm and Total distance = 352 m = 35200 cm
∴ Distance covered by wheel = n x circumference of wheel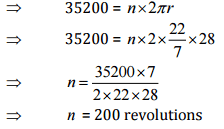
Thus, the wheel must rotate 200 times to go 352 m.
Q17: The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour?
Sol:
In 1 hour, minute hand completes one round means making a circle.
Radius of the circle (r) = 15 cm
A circumference of circular clock = 2πr
= 2 x 3.14 x 15
= 94.2 cm
Therefore, the tip of the minute hand moves 94.2 cm in 1 hour.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Perimeter and Area- 2
| 1. What is the formula to calculate the area of a rectangle? |  |
| 2. How to find the perimeter of a circle? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. What is the unit of measurement for area? |  |
| 5. How do you calculate the area of an irregular shape? |  |






















