Power Play NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Page 19
Q: Say you can fold a sheet of paper as many times as you wish. What would its thickness be after 30 folds? Make a guess.
Ans: Here, 230 = 1,073,741,824
Final thickness = 0.001 × 1,073,741,824
= 1,073,741.824 cm
= 10,737.41824 meters (1 m = 100 cm)
= 10.74 kilometers (1 km = 1000 m)
Hence, after 30 folds, the thickness of the paper would be approximately 10.74 kilometers.
Page 21
The following table lists the thickness after each fold. Observe that the thickness doubles after each fold.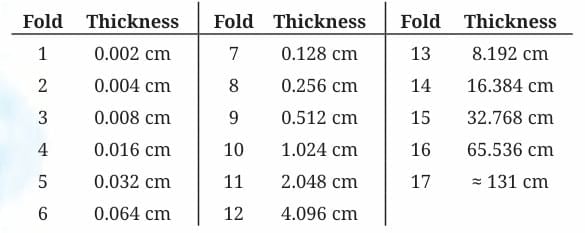
(We use the sign ‘≈’ to indicate ‘approximately equal to’.)
After 10 folds, the thickness is just above 1 cm (1.024 cm).
After 17 folds, the thickness is about 131 cm (a little more than 4 feet).
Q: Now, what do you think the thickness would be after 30 folds? 45 folds? Make a guess.
Ans: The thickness of the paper doubles after each fold. To find the thickness after 30 folds, we can use the formula:
Thickness after n folds =0.002 × 2(n−1)
For 30 folds, the calculation is:
Thickness after 30 folds = 0.002 × 229 = 0.002 × 536,870,912 = 1,073,741.82 cm
So, the thickness after 30 folds is approximately 1,073,741.82 cm or 10.7 kilometers.
Q: Fill the table below:
After 26 folds, the thickness is approximately 670 m. Burj Khalifa in Dubai, the tallest building in the world, is 830 m tall.
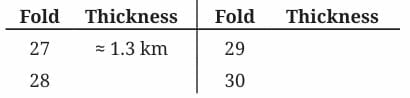
After 30 folds, the thickness of the paper is about 10.7 km, the typical height at which planes fly. The deepest point discovered in the oceans is the Mariana Trench, with a depth of 11 km.
Ans: Do it Yourself.
Page 22
Which expression describes the thickness of a sheet of paper after it is folded 10 times? The initial thickness is represented by the letter-number v.
(i) 10v
(ii) 10 + v
(iii) 2 × 10 × v
(iv) 210
(v) 210v
(vi) 102 v
Answer:
Each time a sheet of paper is folded, its thickness doubles. So after:
1 fold → thickness = 2 × v
2 folds → thickness = 22 × v
Similarly, 10 folds → thickness = 210 × v
Hence, the correct option is (v) 210 × v.
When we have a negative number like -2 and we raise it to different powers, the sign of the result depends on whether the power is even or odd.
A negative number raised to an even power gives a positive result.
(-2)2 = (-2) × (-2) = 4
A negative number raised to an odd power gives a negative result.
(-2)3 = (-2) × (-2) × (-2) = -8.
What is (– 1)5 ? Is it positive or negative? What about (– 1)56?
Answer:
(-1)5 = -1, which is negative. [∵ (-1)0dd number = -1 → Negative]
(-1)56 = +1, which is positive. [∵ (-1)even number = +1 → positive]
Is (– 2)4 = 16? Verify.
Answer:
(-2)4 = (-2) × (-2) × (-2) × (-2)
= 4 × 4
= 16
Yes, (-2)4 = 16.
What is 02, 05?
Answer:
02 = 0 × 0 = 0
05 = 0 × 0 × 0 × 0 × 0 = 0
What is 0n?
Answer:
0n = 0 × 0 × 0 × …… n times = 0
Figure it Out
(i) 6 × 6 × 6 × 6 (ii) y × y
(iii) b × b × b × b (iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a (vi) a × a × a × c × c × c × c × d
(i) 64
(ii) y2
(iii) b4
(iv) 52 × 73
(v) 22 × a2
(vi) a3 × c4 × d
(i) 648 (ii) 405 (iii) 540 (iv) 3600
(i) Prime factors of 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
Exponential form of 648 = 23 × 34
(ii) Prime factors of 405 = 3 × 3 × 3 × 3 × 5
Exponential form of 405 = 34 × 5
(iii) Prime factors of 540 = 2 × 2 × 3 × 3 × 3 × 5
Exponential form of 540 = 22 × 33 × 5
(iv) Prime factors of 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
Exponential form of 3600 = 24 × 32 × 52
(i) 2 × 103 (ii) 72 × 23 (iii) 3 × 44 (iv) (– 3)2 × (– 5)2
(v) 32 × 104 (vi) (– 2)5 × (– 10)6
(i) 2 × 103 = 2 × 10 × 10 × 10
= 2 × 1000
= 2000
(ii) 72 × 23 = 7 × 7 × 2 × 2 × 2
= 49 × 8
= 392
(iii) 3 × 44 = 3 × 4 × 4 × 4 × 4
= 3 × 256
= 768
(iv) (-3)2 × (-5)2 = -3 × -3 × -5 × -5
= 9 × 25
= 225
Negative numbers raised to even powers become positive.
(v) 32 × 104 = 3 × 3 × 10 × 10 × 10 × 10
= 9 × 10,000
= 90,000
(vi) (-2)5 × (-10)6 = -2 × -2 × -2 × -2 × -2 × 10 × 10 × 10 × 10 × 10 × 10
= (-32) × (10,00,000)
= -3,20,00,000
Odd power of a negative number remains negative, even power becomes positive.
Page 24
Q. Use this observation to compute the following. (i) 29 (ii) 57 (iii) 46
Answer:
(i) 29 = 23 × 23 × 23
= 8 × 8 × 8
= 512
(ii) 57 = 52 × 52 × 52 × 5
= 25 × 25 × 25 × 5
= 625 × 125
= 78125
(iii) 46 = 42 × 42 × 42
= 16 × 16 × 16
= 256 × 16
= 4096
(i) 86 (ii) 715 (iii) 914 (iv) 58
(i) 86 = (82)3 = (83)2
(ii) 715 = (73)5 = (75)3
(iii) 914 = (92)7 = (97)2
(iv) 58 = (52)4 = (54)2
Page 25
Q. In the middle of a beautiful, magical pond lies a bright pink lotus. The number of lotuses doubles every day in this pond. After 30 days, the pond is completely covered with lotuses. On which day was the pond half full?
Answer:
- The number of lotuses doubles daily.
- On day 30, the pond is fully covered.
- Since the lotuses double every day, the day before (day 29), the pond must have been half full.
- This is because doubling the lotuses from day 29 to day 30 makes the pond fully covered.
The pond was half full on day 29.
Q. Write the number of lotuses (in exponential form) when the pond was —
(i) fully covered (ii) half covered
Answer:
Let’s assume we start with 1 lotus on day 1.
The number of lotuses doubles each day, so:
- On day 1: 1 lotus
- On day 2: 1 × 2 = 2 lotuses
- On day 3: 2 × 2 = 4 lotuses
- On day 4: 4 × 2 = 8 lotuses
- And so on.
This pattern shows the number of lotuses on day “n” is 2(n-1).
For day 30 (fully covered):
- Number of lotuses = 2(30-1) = 229.
For day 29 (half covered):
- Number of lotuses = 2(29-1) = 228.
- (i) Fully covered (day 30): 229 lotuses
- (ii) Half covered (day 29): 228 lotuses
Q. Simplify 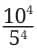 and write it in exponential form.
and write it in exponential form.
Answer: 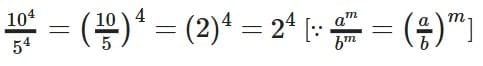
Page 26
How Many Combinations
Q: Roxie has 7 dresses, 2 hats, and 3 pairs of shoes. How many different ways can Roxie dress up?
Ans: 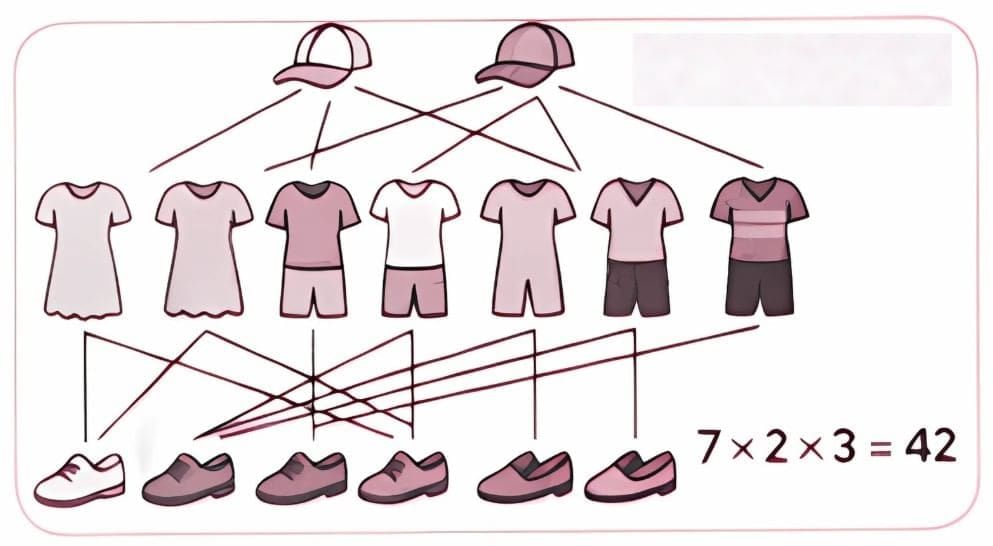 Roxie, pick one dress from the 7 options.
Roxie, pick one dress from the 7 options.
Pair it with one hat from the 2 choices.
Then choose one pair of shoes from the 3 styles.
Each piece is independent, so we multiply the choices = 7 × 2 × 3 = 42
That means Roxie has 42 unique combinations to show off!
Q: Estu and Roxie came across a safe containing old stamps and coins that their great-grandfather had collected. It was secured with a 5-digit password. Since nobody knew the password, they had no option except to try every password until it opened. They were unlucky and the lock only opened with the last password, after they had tried all possible combinations. How many passwords did they end up checking?
Answer: Password Possibilities
Each digit can be any number from 0 to 9 → 10 choices per digit
Total combinations for a 5-digit password = 105 = 100,000
So Estu and Roxie ended up checking:
100,000 passwords…with the safe finally unlocking on that very last one.
Q: Estu says, “Next time I will buy a lock that has 6 slots with the letters A to Z. I feel it is safer.”
How many passwords are possible with such a lock?
Answer: Password Possibilities
Each slot has 26 choices (letters A-Z)
Total combinations: 266 = 308,915,776
So with Estu’s upgraded lock, there are 308,915,776 possible passwords.
Q: Think about how many combinations are possible in different contexts. Some examples are — (i) Pincodes of places in India — The Pincode of Vidisha in Madhya Pradesh is 464001. The Pincode of Zemabawk in Mizoram is 796017.
(ii) Mobile numbers.
(iii) Vehicle registration numbers.
Try to find out how these numbers or codes are allotted/generated.
Answer:
(i) PIN Codes in India
India uses a 6-digit Postal Index Number (PIN) system introduced in 1972.
Structure:
- 1st digit: Region (9 zones total)
- 2nd digit: Sub-region
- 3rd digit: Sorting district
- Last 3 digits: Specific post office
Combinations:
- Theoretically: 106 = 1,000,000 combinations
- Practically: Only valid combinations are used based on geography and postal infrastructure.
e.g, 464001 → Vidisha, Madhya Pradesh
796017 → Zemabawk, Mizoram
(ii) Mobile numbers in India
Indian mobile numbers are 10 digits, starting with digits 6-9.
Structure:
- 1st digit: Must be 6, 7, 8, or 9
- Remaining 9 digits: Any number from 0-9
Combinations:
4 × 109 = 4,000,000,000 possible mobile numbers
Allocation:
- Managed by the Department of Telecommunications
- Prefixes (like 91x, 98x) are assigned to different telecom operators.
(iii) Vehicle Registration Numbers
Vehicle numbers follow a format like DL 01 AB 1234.
Structure:
- 2 letters: State/UT code (e.g., DL for Delhi)
- 2 digits: RTO code
- 1-2 letters: Series
- 4 digits: Unique vehicle number
Combinations:
Varies by state and RTO, but for one RTO:
262 letter combinations × 104 numbers = 676 × 10,000 = 6,760,000 combinations per RTO
Allocation:
- Managed by the Ministry of Road Transport & Highways via the Parivahan portal.
- Fancy numbers can be bid for, and older vehicles may require re-registration.
Page 27
So, dividing powers is just like reducing the number of times we multiply the base.
This rule helps us solve problems faster and understand how powers behave when we break them down.
Q: In a generalised form, na ÷ nb = na – b, where n ≠ 0 and a and b are counting numbers and a > b. Why can’t n be 0?
Answer: 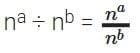 This can also be written as
This can also be written as 
So if n = 0, both the numerator and denominator involve multiplying by zero, and especially the denominator becomes zero, like: 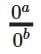
If b > 0, then 0b = 0, and we’re dividing by zero, which is undefined in mathematics.
For example, 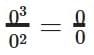 which has no defined value.
which has no defined value.
Page 29
Consider the following general forms we have identified.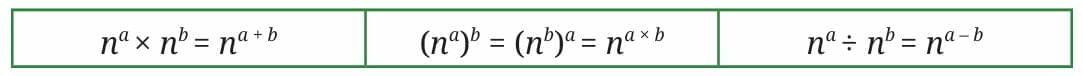
Q. We had required a and b to be counting numbers. Can a and b be any integers? Will the generalised forms still hold true?
Answer: The general forms you identified, known as the laws of exponents, were initially observed for counting numbers (positive integers), but they do indeed hold true when the exponents a and b are any integers (positive, negative, or zero).
Let's verify the two main rules you're asking about with integer exponents.
1. Product of Powers Rule: nᵃ × nᵇ = nᵃ⁺ᵇ
nᵃ × nᵇ = nᵃ⁺ᵇ
This rule states that when you multiply powers with the same base, you add the exponents. Let's test it with a negative exponent.
- Example: Consider 3⁵ × 3⁻².
- Using the definition of a negative exponent:
3⁻² is the same as 1 / 3². So the expression is 3⁵ × (1/3²) = 3⁵ / 3².
This means (3×3×3×3×3) / (3×3) = 3³ = 27. - Using the generalized rule:
We add the exponents: 3⁵⁺⁽⁻²⁾ = 3³ = 27.
As you can see, both methods yield the same result. The rule works perfectly with integers.
2. Power of a Power Rule: (nᵃ)ᵇ = nᵃᵇ
(nᵃ)ᵇ = nᵃᵇ
This rule states that to raise a power to another power, you multiply the exponents. Let's test this with a negative exponent as well.
- Example: Consider (4²)⁻³.
- Using the definition of a negative exponent:
The expression means 1 / (4²)³.
This is 1 / (4² × 4² × 4²) = 1 / 4²⁺²⁺² = 1 / 4⁶. - Using the generalized rule:
We multiply the exponents: 4²ˣ⁽⁻³⁾ = 4⁻⁶.
Since 4⁻⁶ is the same as 1 / 4⁶, the results match.
These rules hold true because of the mathematical definitions for zero and negative exponents:
- Zero Exponent: n⁰ = 1
- Negative Exponent: n⁻ᵃ = 1 / nᵃ
(i) 2– 4 (ii) 10– 5 (iii) (– 7)–2 (iv) (– 5)– 3 (v) 10– 100
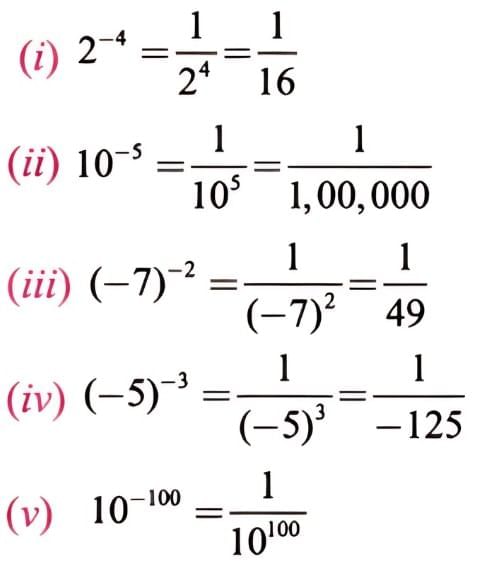
(i) 2– 4 × 27 (ii) 32 × 3– 5 × 36 (iii) p3 × p–10 (iv) 24 × (– 4) – 2 (v) 8p × 8q
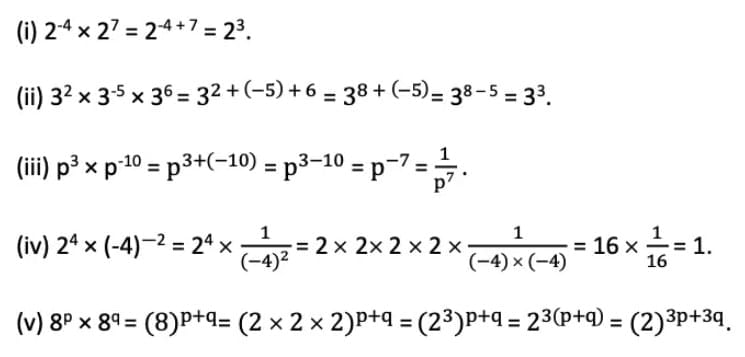
Power Lines
Let us arrange the powers of 4 along a line.
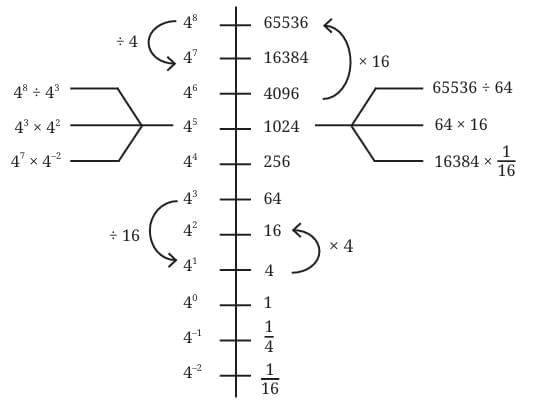
Q. How many times larger than 4–2 is 42?
Answer:
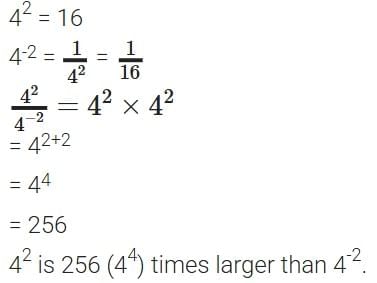
Q. Use the power line for 7 to answer the following questions.

Answer:
2,401 × 49 = ?
- 2,401 is 7⁴ and 49 is 7².
- 7⁴ × 7² = 7⁴⁺² = 7⁶
- From the power line, 7⁶ is 117,649.
49³ = ?
- 49 is 7².
- (7²)³ = 7²ˣ³ = 7⁶
- From the power line, 7⁶ is 117,649.
343 × 2,401 = ?
- 343 is 7³ and 2,401 is 7⁴.
- 7³ × 7⁴ = 7³⁺⁴ = 7⁷
- From the power line, 7⁷ is 823,543.
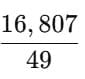 = ?
= ?
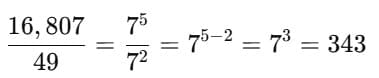
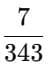 = ?
= ?
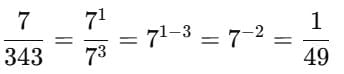
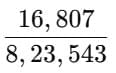 = ?
= ?
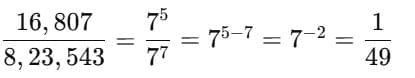
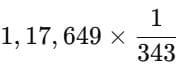 = ?
= ?
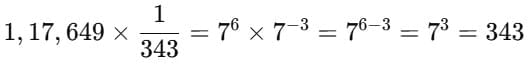
 = ?
= ?
Powers of 10
We have used numbers like 10, 100, 1000, and so on when writing Indian numerals in an expanded form. For example,
47561 = (4 × 10000) + (7 × 1000) + (5 × 100) + (6 × 10) + 1.
This can be written using powers of 10 as
(4 × 104) + (7 × 103) + (5 × 102) + (6 × 101) + (1 × 100).
Q. Write these numbers in the same way: (i) 172, (ii) 5642, (iii) 6374.
Answer:
(i) 172
This number can be broken down by place value: 1 hundred, 7 tens, and 2 ones.
172 = (1 × 10²) + (7 × 10¹) + (2 × 10⁰)
(ii) 5642
This number is composed of 5 thousands, 6 hundreds, 4 tens, and 2 ones.
5642 = (5 × 10³) + (6 × 10²) + (4 × 10¹) + (2 × 10⁰)
(iii) 6374
This number is composed of 6 thousands, 3 hundreds, 7 tens, and 4 ones.
6374 = (6 × 10³) + (3 × 10²) + (7 × 10¹) + (4 × 10⁰)
Page 31
Scientific Notation
Q. Write the large-number facts we read just before in this form (scientific notation).(i) The Sun is located 30,00,00,00,00,00,00,00,00,000 m from the centre of our Milky Way galaxy.
(ii) The number of stars in our galaxy is 1,00,00,00,00,000.
(iii) The mass of the Earth is 59,76,00,00,00,00,00,00,00,00,00,000 kg.
(i) 3 × 1022 m (ii) 1 × 1011 stars (iii) 5.976 × 1024 kg
Page 32
- The distance between the Sun and Saturn is 14,33,50,00,00,000 m = 1.4335 × 1012 m.
- The distance between Saturn and Uranus is 14,39,00,00,00,000 m = 1.439 × 1012 m.
- The distance between the Sun and Earth is 1,49,60,00,00,000 m = 1.496 × 1011 m.

Answer: Compare and see which one has the least power of 10.
- Sun to Saturn: 1.4335 × 1012 m -> 12
- Saturn to Uranus: 1.439 × 1012 m -> 12
- Sun to Earth: 1.496 × 1011 m -> 11
So, the distance between the Sun and the Earth is the smallest.
Q: The number line below shows the distance between the Sun and Saturn (1.4335 × 1012 m). On the number line below, mark the relative position of the Earth. The distance between the Sun and the Earth is 1.496 × 1011 m.
Answer: Do it Yourself!
(i) 59,853 (ii) 65,950 (iii) 34,30,000 (iv) 70,04,00,00,000
(i) 59,853 = 5.9853 × 104
(ii) 65,950 = 6.595 × 104
(iii) 34,30,000 = 3.43 × 106
(iv) 70,04,00,00,000 = 7.004 × 1010
Page 33
Did You Ever Wonder?
Q: Roxie wonders, “Instead of jaggery if we use 1-rupee coins, how many coins are needed to equal my weight?”. How can we find out?
Guessing: Make an instinctive (quick) guess of what the answer could be, without any calculations.
Answer: Guessing
Roxie is 13 years old, so we might guess her weight is around 40 to 45 kg.
If we assume the price of jaggery is ₹ 70 per kg, then
No. of 1 rupee coins = 45 × 70 = 3150
Page 34
Q: Calculating using estimation and approximation —
(i) Describe the relationships among the quantities that are needed to find the answer.
(ii) Make reasonable assumptions and approximations if the required information is not available.
(iii) Compute and find the answer (and check how close your guess was).
Answer:
(i) Describing relationships between quantities.
To find out how many ₹ 1 coins match Roxie’s weight in rupee value, we need to identify:
Roxie’s weight in kg
Price of 1 kg of Jaggery
Value of donation = weight × price per kg
Number of ₹ 1 coins needed = value in rupees ÷ 1
(ii) Assumptions and approximations since exact data isn’t provided.
Let’s use reasonable estimates:
Roxie’s weight ~ 45 kg (typical for a 13-year-old)
Cost of 1 kg jaggery ~ ₹ 70 (average market rate)
Value of jaggery = 45 × 70 = ₹ 3150
(iii) Number of ₹ 1 coin needed = ₹ 3150 ÷ ₹ 1 = 3150 coins
So, Roxie would need approximately 3150 ₹ 1 coins to match the value of jaggery equal to her weight.
Q: Would the number of coins be in hundreds, thousands, lakhs, crores, or even more? Make an instinctive guess.
Ans: A quick, instinctive guess using some smart thinking
Roxie’s weight is about 45 kg, and jaggery costs ₹ 70 per kg.
∴ Total cost = 45 × ₹ 70 = ₹ 3150
If we are using ₹ 1 coins, then 3150 coins are needed, which falls in the thousand range.
Hence, thousands of coins would be needed, not lakhs or crores, but more than hundreds.
Q: Estu asks, “What if we use 5-rupee coins or 10-rupee notes instead? How much money could it be?
Ans: We already calculated the total donation value of ₹ 1140.
No. of ₹ 5 coins = 1140 ÷ 5 = 228
Number of ₹ 10 notes = 1140 ÷ 10 = 114
Estu says, “When I become an adult, I would like to donate notebooks worth my weight every year”. Roxie says, “When I grow up, I would like to do annadāna (offering grains or meals) worth my weight every year”.
Q: How many people might benefit from each of these offerings in a year? Again, guess first before finding out.
Answer: Quick Guess
Estu’s notebook donation may benefit 100 to 200 students could benefit each year.
Roxie’s meal offering is perhaps enough grains or meals to feed 150 to 300 people annually.
Estimate and calculate
Assumptions:
Estu’s weight ~ 38 kg
Cost of 1 notebook ~ ₹ 20
Roxie’s weight is ~ 45 kg
Cost of 1 kg of grain or meal donations ~ ₹ 30
Meal cost per person per day ~ ₹ 15
Estu’s donation: Notebooks worth her weight
Value of donation = 38 × ₹ 20 = ₹ 760
If each student needs 2 notebooks:
No. of students helped = ₹ 760 ÷ ₹ 40 = 19
19 students could receive notebooks each year.
Roxie’s donation: Grains or Meals worth her weight
Value of donation = 45 × ₹ 30 = ₹ 1350
Each meal costs = ₹ 15
∴ No. of people to whom meal can be provided = ₹ 1350 ÷ 15 = 90
90 people could receive a single meal, or fewer people could eat multiple meals per year.
Roxie and Estu overheard someone saying — “We did pādayātra for about 400 km to reach this place! We arrived early this morning.”
Q: How long ago would they have started their journey? Find answers by making necessary assumptions and approximations. Do guess first before calculating to check how close your guess was!
Answer: Guessing
If someone walked 400 km on foot, how long might it take?
Let us guess they walked about 25-30 km per day.
∴ Rough guess for number of days = 400 ÷ 25 = 16 days
Or maybe 13-20 days, depending on speed and rest.
Estimating and Calculating
Let daily distance walked = 30 km
Distance covered = 400 km
Number of days = 400 ÷ 30
= 13.3 days
~ 13 to 14 days
Page 35
Q: How many times can a person circumnavigate (go around the world) the Earth in their lifetime if they walk non-stop? Consider the distance around the Earth as 40,000 km.
Answer: Assumptions
Circumference of Earth = 40,000 km
Average walking speed = 5 km/hr
Maximum walking hours per day = 8 hours (approx.) years spent walking.
Let’s assume an active span of 60 years (ages 15 to 75)
Distance covered in 1 day = 8 × 5 = 40 km
Total days walked over = 60 × 365 = 21,900 days
Total lifetime distance walked = 21900 × 40 = 876000 km
Earth circumnavigations = 876000 + 40,000 = 21.9 times
Linear Growth vs. Exponential Growth
Q: Can you come up with some examples of linear growth and of exponential growth?
Answer: Linear Growth Examples
- Pocket money increase: If our parents add ₹ 50 to our savings every week, it’s growing linearly: ₹ 50, ₹ 100, ₹ 150, and so on.
- Steps Climbed: Climbing 10 steps every minute means we’ve climbed 10, 20, 30,… that’s a linear increase.
- Plant height: If a bamboo plant grows 5 cm each day, it follows linear patterns 5 cm, 10 cm, 15 cm, …..
Exponential Growth Examples
- Virus speed: If 1 person infects 2 others, and each of them infects 2 more… the numbers explode quickly: 1, 2, 4, 8, 16,…
- Magic coins doubling: If we get 1 coin today, 2 coins tomorrow, then 4, 8, 16,… that’s exponential.
- Bacterial growth: If bacteria double every hour, a single one can become millions in just a day!
Page 38
Q: With a global human population of about 8 × 109 and about 4 × 105 African elephants, can we say that there are nearly 20,000 people for every African elephant?
Answer: Global human population = 8 × 109 = 8,00,00,00,000
Number of African elephants = 4 × 105 = 4,00,000
Number of people per elephants = 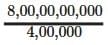 = 20,000
= 20,000
(i) How many ants are there for every human in the world?
(ii) If a flock of starlings contains 10,000 birds, how many flocks could there be in the world?
(iii) If each tree had about 104 leaves, find the total number of leaves on all the trees in the world. (iv) If you stacked sheets of paper on top of each other, how many would you need to reach the Moon?
(i) Estimated number of ants = 2 × 1016 (20 quadrillion)
Estimated human population = 8 × 109
Number of ants per person = 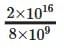 = 0.25 × 107
= 0.25 × 107
= 2.5 × 106
(ii) Estimated number of starlings = 3.1 × 108 (310 millions)
Number of birds in each flock = 1 × 104
Number of flocks in the world = 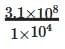 = 3.1 × 104
= 3.1 × 104
(iii) Estimated number of trees = 3 × 1012
Number of leaves on each tree = 1 × 104
Total number of leaves on all the trees in the world = 3 × 1012 × 1 × 104 = 3 × 1016
(iv) Distance of Moon = 3.84 × 108 m
Thickness of one sheet of paper = 1 × 10-4 m
Number of sheets required to reach moon = 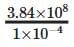 = 3.84 × 1012
= 3.84 × 1012
Page 39
Q: If you have lived for a million seconds, how old would you be?
Answer:
1 minute = 60 seconds
1 hour = 60 minutes
= 60 × 60 seconds
= 3600 seconds
1 day = 24 hours
= 24 × 3600 seconds
= 86,400 seconds
You lived for = 1 million seconds = 10,00,000 seconds
Number of days = 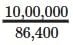 ~ 11.57 days
~ 11.57 days
Page 40
(i) 105 seconds and (ii) 106 seconds. Write them in scientific notation.
(i) Events lasting ~ 105 seconds (~ 1.16 days)
(a) Multi-stage cycling race leg (like one stage of the Tour de France)
Duration: 1 × 105 seconds
(b) Filming a short movie or documentary:
Shooting schedule ~ 1.2 × 105 seconds
(c) College entrance exams conducted over 2 full days (including breaks)
Total time of exam ~ 1.1 × 105 seconds
(ii) Events lasting ~ 106 seconds (~ 11.57 days)
(a) International space station crew adjustment period:
Time for acclimatization ~ 1 × 106 seconds
(b) Large festival duration (e.g., Kumbh Mela or Olympics opening events):
Full festivity span ~ 1 × 106 seconds
(c) Incubation period for chicken eggs:
Time until hatching ~ 1.2 × 106 seconds
Page 41
15 million years = 15 × 106 years.
1 year ≈ 3.1536 × 107 seconds.
15 × 106 years × 3.1536 × 107 seconds/year ≈ 47.304 × 1013 seconds
= 4.7304 × 1014 seconds.
Page 42
470 million years = 470 × 106 years = 4.7 × 108 years.
1 year ≈ 3.1536 × 107 seconds. 4.7 × 108 years × 3.1536 × 107 seconds/year
≈ 14.822 × 1015 seconds = 1.4822 × 1016 seconds.
(i) If one star is counted every second, how long would it take to count all the stars in the universe? Answer in terms of the number of seconds using scientific notation.
(ii) If one could drink a glass of water (200 ml) every 10 seconds, how long would it take to finish the entire volume of water on Earth?
(i) Estimated number of stars in the observable universe: 1 × 1024 stars (1 septillion)
If you count 1 star per second, then:
Time required = 1 × 1024 seconds
(ii) Total volume of water on Earth: 1.386 × 109 km3
Convert to milliliters: 1.386 × 109 km3
= 1.386 × 109 × 1015 ml
= 1.386 × 1024 ml
Capacity of each glass = 200 ml
Time taken to drink per glass = 10 seconds
Total number of glasses = 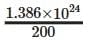 = 6.93 × 1021
= 6.93 × 1021
Total time used = 6.93 × 1021 × 10 = 6.93 × 1022 seconds
Figure it Out (Page 44)
2224 ÷ 432 = 2224 ÷ (22)32 = 2224 ÷ 264 = 2(224-64) = 2160.
To find the units digit of 2160, observe the pattern of units digits of powers of 2:
21 = 2
22 = 4
23 = 8
24 = 16 (units digit is 6)
25 = 32 (units digit is 2)
The pattern of units digits is 2, 4, 8, 6, and it repeats every 4 powers.
Divide the exponent 160 by 4: 160 ÷ 4 = 40 with a remainder of 0.
A remainder of 0 means the units digit is the same as the 4th power in the cycle, which is 6. So, the units digit in the value of 2224 ÷ 432 is 6.
Number of containers added every day = 1
Number of containers after 40 days = 40 containers
Number of bottles in a container = 5
Total bottles in 40 containers = 5 × 40 = 200 bottles
Therefore, there would be 200 bottles after 40 days.
(i) 643 (ii) 1928 (iii) 32–5
(i) 64³
64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
643 = (26)3 = 218
Three different ways:
1. 643 = 218 = 29 × 29
2. 643 = 218 = 210 × 28
3. 643 = 218 = 26 × 26 × 26
(ii) 192⁸
First, find the prime factors of 192, which are 2⁶ × 3. Therefore, 192⁸ = (2⁶ × 3)⁸. Using the exponent rules, we can write this in several ways.
Way 1: By distributing the exponent to each factor inside the parenthesis:
(2⁶)⁸ × 3⁸ = 2⁴⁸ × 3⁸Way 2: By changing the base of the first term:
(2²)²⁴ × 3⁸ = 4²⁴ × 3⁸Way 3: By grouping common exponents after splitting a power:
2⁴⁰ × 2⁸ × 3⁸ = 2⁴⁰ × (2 × 3)⁸ = 2⁴⁰ × 6⁸
(iii) 32⁻⁵
32 = 2 × 2 × 2 × 2 × 2 = 25
32-5 = (25)-5 = 2-25
Three different ways:
1. 32-5 = 2-25 = 2-15 × 2-10
2. 32-5 = 2-25 = 2−5 × 2−5 × 2−5 × 2−5 × 2−5
3. 32-5 = 2-25 = 2-5 × 2-20
(i) Cube numbers are also square numbers.
(ii) Fourth powers are also square numbers.
(iii) The fifth power of a number is divisible by the cube of that number.
(iv) The product of two cube numbers is a cube number.
(v) q46 is both a 4th power and a 6th power (q is a prime number).
(i) Cube numbers are also square numbers.
Only Sometimes True
Reasoning: A number n³ is a cube number. For it to also be a square number, it must be possible to write it as m² for some integer m.
When it is true: Consider the cube number 64. 64 = 4³, and it is also a square number because 64 = 8². This works because the base number (4) is itself a perfect square (2²). If we take any base that is a square number, say k², its cube will be (k²)³ = k⁶. This can be rewritten as (k³)², which is a perfect square.
When it is false: Consider the cube number 8. 8 = 2³, but 8 is not a perfect square. Similarly, 27 = 3³ is not a perfect square. This happens whenever the base is not a perfect square.
Since the statement is true for some numbers (like 1, 64, 729) but false for others (like 8, 27, 125), it is only sometimes true.
(ii) Fourth powers are also square numbers.
Always True
Reasoning: A fourth power of a number n is n⁴. Using the laws of exponents, we can rewrite this expression:
n⁴ = n²⁺² = n² × n² = (n²)²
Since n² is an integer (if n is an integer), (n²)² is the square of an integer. Therefore, any fourth power is also a perfect square.
Example: 3⁴ = 81, which is 9² (and 9 = 3²).
Example: 5⁴ = 625, which is 25² (and 25 = 5²).
(iii) The fifth power of a number is divisible by the cube of that number.
Always True
Reasoning: Let the number be n. Its fifth power is n⁵ and its cube is n³. To check for divisibility, we divide n⁵ by n³. Using the quotient rule for exponents (nᵃ / nᵇ = nᵃ⁻ᵇ):
n⁵ / n³ = n⁵⁻³ = n²
For any non-zero integer n, the result n² is also an integer. Since the division results in an integer, n⁵ is always divisible by n³.
(iv) The product of two cube numbers is a cube number.
Always True
Reasoning: Let the two cube numbers be a³ and b³. Their product is a³ × b³. Using the laws of exponents, we can combine this into a single term:
a³ × b³ = (a × b)³
Since a and b are integers, their product (a × b) is also an integer. Therefore, (a × b)³ is, by definition, a cube number.
Example: 8 × 27 = 2³ × 3³ = (2 × 3)³ = 6³ = 216.
(v) q⁴⁶ is both a 4th power and a 6th power (q is a prime number).
Never True
Reasoning: For an expression xᵃ to be a perfect bth power, the exponent a must be a multiple of b.
Is it a 4th power? For q⁴⁶ to be a 4th power, 46 must be divisible by 4. Since 46 ÷ 4 = 11.5, which is not an integer, q⁴⁶ is not a 4th power.
Is it a 6th power? For q⁴⁶ to be a 6th power, 46 must be divisible by 6. Since 46 ÷ 6 ≈ 7.67, which is not an integer, q⁴⁶ is not a 6th power.
Since q⁴⁶ is neither a 4th power nor a 6th power, it can't possibly be both. Therefore, the statement is never true.
5. Simplify and write these in the exponential form.
Answer:
(i) 10⁻² × 10⁻⁵
When multiplying powers with the same base, you add the exponents (nᵃ × nᵇ = nᵃ⁺ᵇ).
10⁻² × 10⁻⁵ = 10⁻²⁺⁽⁻⁵⁾ = 10⁻⁷(ii) 5⁷ ÷ 5⁴
When dividing powers with the same base, you subtract the exponents (nᵃ ÷ nᵇ = nᵃ⁻ᵇ).
5⁷ ÷ 5⁴ = 5⁷⁻⁴ = 5³(iii) 9⁻⁷ ÷ 9⁴
Using the same division rule as above:
9⁻⁷ ÷ 9⁴ = 9⁻⁷⁻⁴ = 9⁻¹¹(iv) (13⁻²)⁻³
To raise a power to another power, you multiply the exponents ((nᵃ)ᵇ = nᵃᵇ).
(13⁻²)⁻³ = 13⁽⁻²⁾ˣ⁽⁻³⁾ = 13⁶(v) (m⁵n¹²) (mn)⁹
m5n12 × m9n9 = m5+9n12+9 = m14n21
6. If 12² = 144 what is
(i) (1.2)²
(ii) (0.12)²
(iii) (0.012)²
(iv) 120²
Answer:
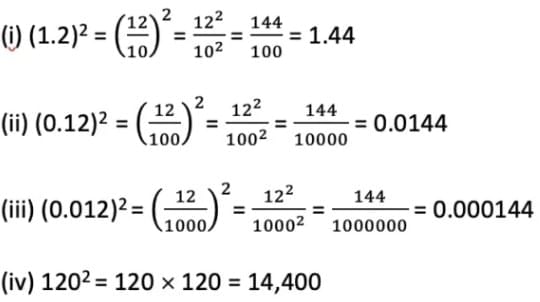
Figure it Out (Page 45)
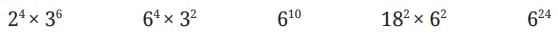
Answer:

Explanation:
(i) 24 × 36
(ii) 64 × 32 = (2 × 3)4 × 32 = 24 × 34 × 32 = 24 × 36
(iii) 610 = (2 × 3)10 = 210 × 310
(iv) 182 × 62 = (2 × 3 × 3)2 × (2 × 3)2 = 22 × 32 × 32 × 22 × 32 = 24 × 36
(v) 624 = (2 × 3)24 = 224 × 324
Therefore, 24 × 36, 64 × 32, and 182 × 62 are the same.
Q. 8. Identify the greater number in each of the following— (i) 4³ or 3⁴ (ii) 2⁸ or 8² (iii) 100² or 2¹⁰⁰
Answer:
(i) To compare 4³ and 3⁴, we calculate their values.
4³ = 4 × 4 × 4 = 64.
3⁴ = 3 × 3 × 3 × 3 = 81.
Since 81 is greater than 64, 3⁴ is the greater number.
(ii) To compare 2⁸ and 8², we calculate their values.
2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256.
8² = 8 × 8 = 64.
Since 256 is greater than 64, 2⁸ is the greater number.
(iii) To compare 100² and 2¹⁰⁰, we can evaluate or estimate their values.
100² = 100 × 100 = 10,000.
2¹⁰⁰ can be written as (2¹⁰)¹⁰. Since 2¹⁰ = 1024, 2¹⁰⁰ = (1024)¹⁰.
Clearly, (1024)¹⁰ is a vastly larger number than 10,000. Therefore, 2¹⁰⁰ is the greater number.
Q. 9. A dairy plans to produce 8.5 billion packets of milk in a year. They want a unique ID (identifier) code for each packet. If they choose to use the digits 0–9, how many digits should the code consist of?
Answer:
Total no. of packets produced in a year = 8.5 billion
∴ Number of codes required = 8.5 × 109 codes
For ID digits to be taken from 0 to 9.
So each digit has 10 choices.
To make code with n digits, the total number of possible codes = 10n
∴ 10n ≥ 8.5 × 109
109 = 1,00,00,00,000
The smallest value of n that satisfies
10n ≥ 8.5 × 109 is 10.
Hence number of digits the code should consist of 1010.
Q. 10. 64 is a square number (8²) and a cube number (4³). Are there other numbers that are both squares and cubes? Is there a way to describe such numbers in general?
Answer:
Yes, there are other numbers that are both perfect squares and perfect cubes. Such numbers can be described in general as perfect sixth powers.
A number that is a square has prime factors with even exponents, and a number that is a cube has prime factors with exponents that are multiples of three. For a number to be both, its prime factors' exponents must be multiples of both 2 and 3, which means they must be multiples of 6.
Therefore, any number of the form n⁶, where 'n' is an integer, will be both a square and a cube.
- 1 (since 1⁶ = 1, which is 1² and 1³)
- 64 (since 2⁶ = 64, which is 8² and 4³)
- 729 (since 3⁶ = 729, which is 27² and 9³)
Q. 11. A digital locker has an alphanumeric (it can have both digits and letters) passcode of length 5. Some example codes are G89P0, 38098, BRJKW, and 003AZ. How many such codes are possible?
Answer:
Number of letters (A-Z) = 26
Number of digits (0-9) = 10
So, each character in the passcode can be any of the 36 alphanumeric characters.
Also, each of the 5 positions has 36 options.
Total codes = 365 = 6,04,66,176
Hence number of possible 5-character alphanumeric passcodes is 6,04,66,176.
Q. 12. The worldwide population of sheep (2024) is about 10⁹, and that of goats is also about the same. What is the total population of sheep and goats?
(i) 209
(ii) 1011
(iii) 1010
(iv) 1018
(v) 2 × 109
(vi) 109 + 109
Answer:
Population of sheep = 109
Population of goats = 109
Total population of sheep and goats = 109 + 109 or 2 × 109
Therefore, (v) 2 × 109 and (vi) 109 + 109 are the correct answers.
Q. 13. Calculate and write the answer in scientific notation:
(i) If each person in the world had 30 pieces of clothing, find the total number of pieces of clothing.
(ii) There are about 100 million bee colonies in the world. Find the number of honeybees if each colony has about 50,000 bees.
(iii) The human body has about 38 trillion bacterial cells. Find the bacterial population residing in all humans in the world.
(iv) Total time spent eating in a lifetime in seconds.
Answer:
(i) Estimated world population: ≈ 8 billion = 8 × 109
Number of pieces of clothing each person had = 30 pieces
Total number of pieces of clothing = 8×109 × 30 = 2.4 × 1011
(ii) Number of bee colonies in the world = 100 million = 1×108
Number of bees in each colony = 50,000 = 5 × 104
Total number of honeybees = 1 × 108 × 5 × 104 = 5 × 1012
(iii) World population ≈ 8 × 109
Number of bacterial cells in human body = 38 trillion = 3.8 × 1013
Total bacterial population residing in all humans in the world = (3.8 × 1013)× (8 × 109) = 30.4 × 1022 = 3.04 × 1023
(iv) Average person’s lifespan = 80 years
Time spent eating daily = 1.5 hours
Total eating time per day in seconds = 1.5 × 3600 = 5400 seconds
Number of days in 80 years = 80 × 365 = 29,200
Total seconds spent eating in a lifetime in seconds = 5400 × 29,200 = 1.5768 × 108
Q. 14. What was the date 1 arab/1 billion seconds ago?
Answer:
1 arab / 1 billion = 109
minutes = 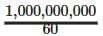 hours =
hours = 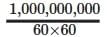 days =
days =  years =
years = 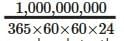 Now, we go back to the calendar.So, it is approx. 31 years, 8 months, and 15 days.
Now, we go back to the calendar.So, it is approx. 31 years, 8 months, and 15 days.
Let today’s date = 1 Jan, 2026
After 31 years and 8 months and 15 days before the date was 24th April, 1994 (approx.)
|
26 videos|133 docs|11 tests
|
FAQs on Power Play NCERT Solutions - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the significance of power play in sports and how does it affect game outcomes? |  |
| 2. How can teams effectively utilize power plays to maximize their performance? |  |
| 3. What are some common strategies used by teams during power plays in hockey? |  |
| 4. How does the concept of power play differ across various sports? |  |
| 5. What role does player discipline play in managing power plays during a game? |  |

















