NCERT Solutions for Class 9 Maths Chapter 8 - Quadrilaterals
Exercise 8.1
Q1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Ans: Given : ABCD is a parallelogram with diagonal AC = diagonal BD.
To prove : ABCD is a rectangle.
Proof : In triangle ABC and BAD:
AB=AB [Common side]
AC=BD [Given]
AD=BC [Opposite sides of a parallelogram are equal]
Therefore, ΔABC ≅ ΔBAD [By SSS congruency rule]
This implies ∠DAB = ∠CBA [By C.P.C.T. (Corresponding Parts of Congruent Triangles)] ... (i)
Since AD∥BC and transversal AB cuts them, the sum of the interior angles on the same side of the transversal is 180°.
∠DAB + ∠CBA = 180° ... (ii)
From equations (i) and (ii), since ∠DAB = ∠CBA, we can substitute:
∠DAB + ∠DAB = 180°
2∠DAB = 180°
∠DAB = 90°
So, ABCD is a parallelogram with one of its angles equal to 90°.
Hence, ABCD is a rectangle.
Q2. Show that the diagonals of a square are equal and bisect each other at right angles.
Ans: Given: A square is given.
To Prove: The diagonals of a square are the same and bisect each other at 90o
Proof: Consider ABCD to be a square.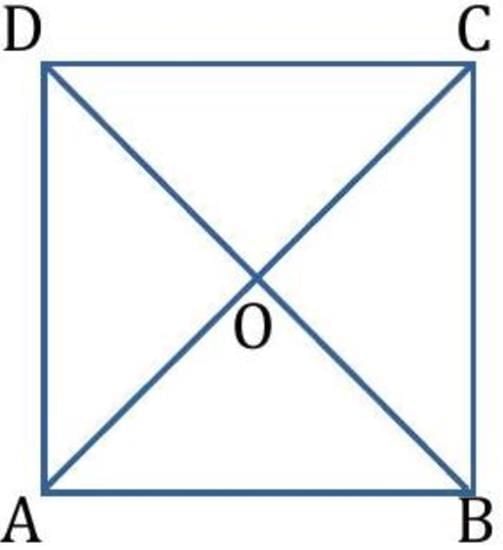
Proof: (i) To prove AC = BD:
In ΔABC and ΔBAD:
AB = BA [Common side]
BC = AD [Opposite sides of square ABCD are equal]
∠ABC = ∠BAD [Each = 90° (since ABCD is a square)]
Therefore, ΔABC ≅ ΔBAD [By SAS Congruence Rule]
Thus, AC = BD ... (i) [By C.P.C.T.]
(ii) To prove that diagonals bisect each other:
In ΔAOD and ΔCOB:
AD = CB [Opposite sides of square ABCD are equal]
∠OAD = ∠OCB [Alternate angles, as AD∥BC and transversal AC intersects them]
∠ODA = ∠OBC [Alternate angles, as AD∥BC and transversal BD intersects them]
Therefore, ΔAOD ≅ ΔCOB [By ASA Congruence Rule]
Thus, OA = OC and OB = OD ... (ii) [By C.P.C.T.]
So, O is the midpoint of AC and BD.
To prove that diagonals bisect each other at right angles:
In ΔAOB and ΔCOB:
AB = CB [Given, sides of a square are equal]
OA = OC [From (ii)]
OB = OB [Common side]
Therefore, ΔAOB ≅ ΔCOB [By SSS Congruence Rule]
Thus, ∠AOB = ∠BOC [By C.P.C.T.]
But ∠AOB + ∠BOC = 180° [Linear pair of angles]
Since ∠AOB = ∠BOC (proved earlier), substitute:
∠AOB + ∠AOB = 180°
2∠AOB = 180°
∠AOB = 180°/2 = 90°
Therefore, ∠AOB = ∠BOC = 90°.
Hence, AC and BD bisect each other at right angles.
Q3. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig.). Show that
(i) It is bisecting ∠C also,
(ii) ABCD is a rhombus
Ans: Given: Diagonal AC bisects ∠A of the parallelogram ABCD.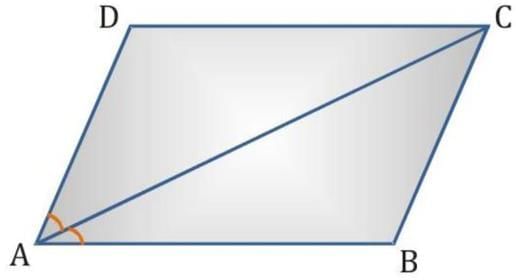
To prove:
(i) AC bisects ∠C also.
(ii) ABCD is a rhombus.
Proof: (i) Since ABCD is a parallelogram, AB∥DC and AC intersects them.
Therefore, ∠BAC = ∠DCA [Alternate interior angles] ... (i)
Similarly, since AD∥BC and AC intersects them.
Therefore, ∠DAC = ∠BCA [Alternate interior angles] ... (ii)
Given that AC bisects ∠A, so ∠BAC = ∠DAC ... (iii)
From (i), (ii), and (iii), we have:
∠DCA = ∠BAC = ∠DAC = ∠BCA
This means ∠DCA = ∠BCA.
Thus, AC bisects ∠C.
(ii) From the relations derived in (i), we have ∠DAC = ∠DCA.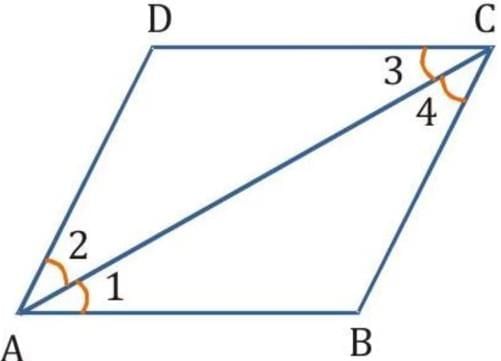
In ΔADC, sides opposite to equal angles are equal.
Therefore, AD = CD.
Also, ABCD is a parallelogram. So, opposite sides are equal: AD=BC and AB=CD.
Combining these, we get: AB = CD = AD = BC.
Hence, ABCD is a rhombus.
Q4. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Ans: Given: ABCD is a rectangle where the diagonal AC bisects ∠A as well as ∠C.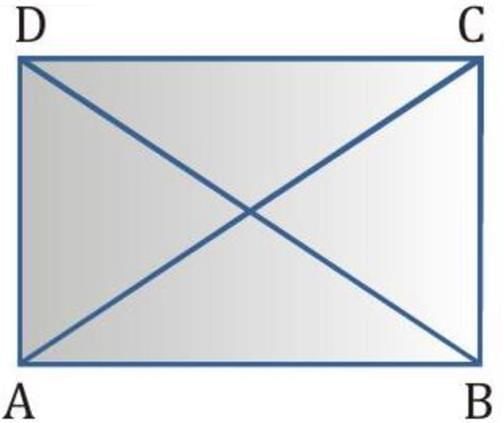
(i) ∠A = ∠C
⇒ 1/2 ∠A = 1/2 ∠C (AC bisects ∠A and ∠C)
⇒ ∠DAC = 1/2 ∠DCA
CD = DA (Sides that are opposite to the equal angles are also equal)
Also, DA = BC and AB = CD (Opposite sides of the rectangle are same)
AB = BC = CD = DA
ABCD is a rectangle with equal sides on all sides.
Hence, ABCD is a square.
(ii) Let us now join BD.
In ΔBCD,
BC = CD (Sides of a square are equal to each other)
∠CDB = ∠CBD (Angles opposite to equal sides are equal)
However, ∠CDB = ∠ABD (Alternate interior angles for AB || CD)
∠CBD = ∠ABD
BD bisects ∠B.
Also, ∠CBD = ∠ADB (Alternate interior angles for BC || AD)
∠CDB = ∠ABD
BD bisects ∠D and ∠B.
Q5. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure).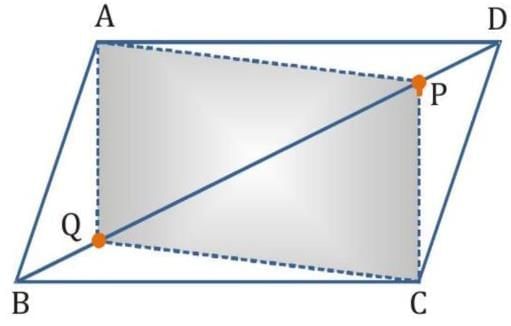 Show that:
Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a Parallelogram
Ans:
(i) In ΔAPD and ΔCQB,
AD = CB (Opposite sides of the parallelogram ABCD)
∠ADP = ∠CBQ (Alternate interior angles for BC || AD)
DP = BQ (Given)
∴ ΔAPD ≅ ΔCQB (Using SAS congruence rule)
(ii) As we had observed that ΔAPD ≅ ΔCQB,
∴ AP= CQ (CPCT)
(iii) In ΔAQB and ΔCPD,
∠ABQ = ∠CDP (Alternate interior angles for AB || CD )
AB = CD (Opposite sides of parallelogram ABCD)
BQ = DP (Given)
∴ ΔAQB ≅ ΔCPD (Using SAS congruence rule)
(iv) Since we had observed that ΔAQB ≅ ΔCPD,
∴ AQ = CP (CPCT)
(v) From the results obtained in (ii) and (iv),
AQ = CP and AP = CQ
APCQ is a parallelogram because the opposite sides of the quadrilateral are equal.
Q6. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure).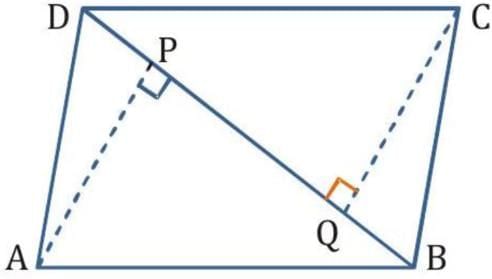 Show that
Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
Ans:
(i) In ΔAPB and ΔCQD,
∠APB = ∠CQD (Each 90°)
AB = CD (The opposite sides of a parallelogram ABCD)
∠ABP = ∠CDQ (Alternate interior angles for AB || CD)
∴ ΔAPB ≅ ΔCQD (By AAS congruency)
(ii) By using
∴ ΔAPB ≅ ΔCQD , we obtain
AP = CQ (By CPCT)
Q7. ABCD is a trapezium in which AB || CD and AD = BC (see the given figure).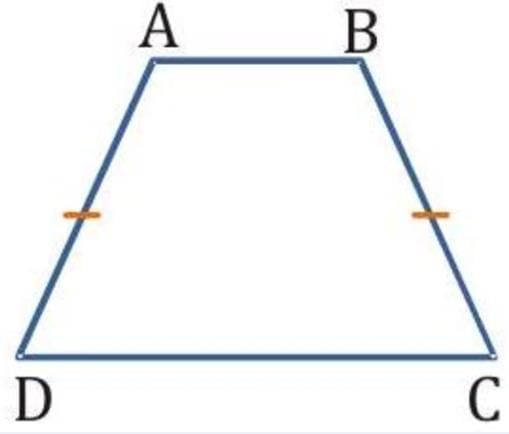 Show that
Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
(Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.)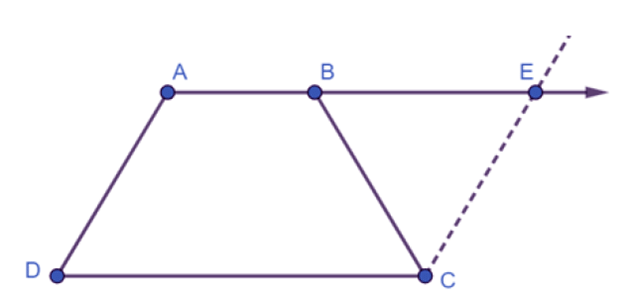 Ans: Let us extend AB by drawing a line through C, which is parallel to AD, intersecting AE at point E. It is clear that AECD is a parallelogram.
Ans: Let us extend AB by drawing a line through C, which is parallel to AD, intersecting AE at point E. It is clear that AECD is a parallelogram.
(i) AD = CE (Opposite sides of parallelogram AECD)
However, AD = BC (Given)
Therefore, BC = CE
∠CEB = ∠CBE (Angle opposite to the equal sides are also equal)
Considering parallel lines AD and CE.
AE is the transversal line for them (Angles on a same side of transversal)
(Using the relation ∠CEB = ∠CBE) ... (1)
However, ∠CBE + ∠CBA = 180° (Linear pair angles) ... (2)
From Equations (1) and (2), we obtain ∠A = ∠B
(ii) AB || CD
Also, ∠C + ∠B = 180° (Angles on a same side of a transversal)
∴ ∠A + ∠D = ∠C + ∠B
However, ∠A = ∠B (Using the result obtained in (i))
∴ ∠C = ∠D
(iii) In ΔABC and ΔBAD,
AB = BA (Common side)
BC = AD (Given)
∠B = ∠A (Proved before)
∴ ΔABC ≅ ΔBAD (SAS congruence rule)
(iv) We had seen that, ΔABC ≅ ΔBAD
∴ AC= BD (By CPCT)
Exercise 8.2
Q1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is diagonal. Show that:
(i) SR || AC and SR = (1/2) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Ans: Given: ABCD is a quadrilateral
To prove: (i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
(i) In ΔADC, S and R are the mid-points of sides AD and CD respectively.
In a triangle, the line segment connecting the midpoints of any two sides is parallel to and half of the third side.
∴ SR || AC and SR = 1/2 AC ... (1)
(ii) In ΔABC, P and Q are mid-points of sides AB and BC respectively. Therefore, by using midpoint theorem,
PQ || AC and PQ = 1/2 AC ... (2)
Using Equations (1) and (2), we obtain
PQ || SR and PQ = SR ... (3)
(iii) From Equation (3), we obtained
PQ || SR and PQ = SR
Clearly, one pair of quadrilateral PQRS opposing sides is parallel and equal. PQRS is thus a parallelogram.
Q2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Ans: 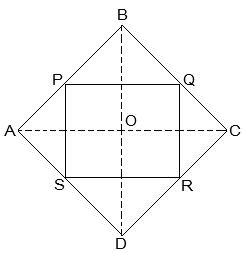
Given: ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
To Prove: PQRS is a rectangle.
Construction:
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC, respectively.
⇒ QR || BD
also,
P and S are the mid points of AD and AB, respectively.
⇒ PS || BD
⇒ QR || PS
PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
PQRS is a rectangle.
Q3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Ans: 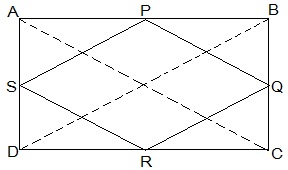 Given: ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
Given: ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
To prove: The quadrilateral PQRS is a rhombus.
Proof: Let us join AC and BD.
In ΔABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC (Mid-point theorem) ... (1)
Similarly, in ΔADC , SR || AR, SR = 1/2 AC (Mid-point theorem) ... (2)
Clearly, PQ || SR and PQ = SR
It is a parallelogram because one pair of opposing sides of quadrilateral PQRS is equal and parallel to each other.
∴ PS || QR , PS = QR (Opposite sides of parallelogram) ... (3)
In ΔBCD, Q and R are the mid-points of side BC and CD respectively.
∴ QR || BD, QR = 1/2 BD (Mid-point theorem) ... (4)
Also, the diagonals of a rectangle are equal.
∴ AC = BD ... (5)
By using Equations (1), (2), (3), (4), and (5), we obtain
PQ = QR = SR = PS
So, PQRS is a rhombus
Q4. ABCD is a trapezium in which AB || DC , BD is a diagonal and E is the mid - point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
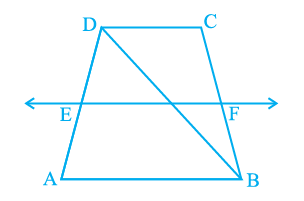
Ans: Given: ABCD is a trapezium in which AB || DC , BD is a diagonal and E is the mid - point of AD. A line is drawn through E parallel to AB intersecting BC at F.
To prove: F is the mid-point of BC.
Proof: Let EF intersect DB at G.
We know that a line traced through the mid-point of any side of a triangle and parallel to another side bisects the third side by the reverse of the mid-point theorem.
In ΔABD, EF || AB and E is the mid-point of AD.
Hence, G will be the mid-point of DB.
As EF || AB, AB || CD,
∴ EF || CD (Two lines parallel to the same line are parallel)
In ΔBCD, GF || CD and G is the mid-point of line BD.
So, by using the converse of mid-point theorem, F is the mid-point of BC.
Q5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
Ans: Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively to prove: The line segments AF and EC trisect the diagonal BD.
To Prove: The line segments AF and EC trisect the diagonal BD.
Proof: ABCD is a parallelogram.
AB || CD
And hence, AE || FC
Again, AB = CD (Opposite sides of parallelogram ABCD)
1/2 AB = 1/2 CD
AE = FC (E and F are mid-points of side AB and CD)
In quadrilateral AECF, one pair of opposite sides (AE and CF) is parallel and the same as each other. So, AECF is a parallelogram.
∴ AF || EC (Opposite sides of a parallelogram)
In ΔDQC, F is the mid-point of side DC and FP || CQ (since AF || EC, and AF intersects BD at P ).
So, by using the converse of mid-point theorem, it can be said that P is the mid-point of DQ.
∴ DP= PQ ... (1)
Similarly, in ΔAPB , E is the mid-point of side AB and EQ || AP (since AF || EC, and EC intersects BD at Q ).
As a result, the reverse of the mid-point theorem may be used to say that Q is the mid-point of PB.
∴ PQ = QB ... (2)
From Equations (1) and (2),
DP = PQ= BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Q6. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB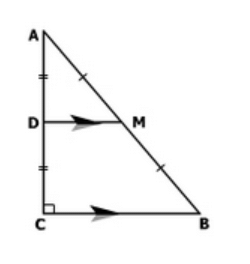 Ans: Given: ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D.
Ans: Given: ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D.
(i) In ΔABC,
It is given that M is the mid-point of AB and MD || BC.
Therefore, D is the mid-point of AC. (Converse of the mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them, therefore,(Co-interior angles)
(iii) Join MC.
In ΔAMD and ΔCMD,
AD = CD (D is the mid-point of side AC)
∠ADM = ∠CDM (Each)
DM = DM (Common)
∴ ΔAMD ≅ ΔCMD (By SAS congruence rule)
Therefore,
AM = CM (By CPCT)
However,
AM = 1/2 AB (M is mid-point of AB)
Therefore, it is said that CM = AM = 1/2 AB.
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 8 - Quadrilaterals
| 1. What are the properties of a quadrilateral? |  |
| 2. How do you calculate the area of a quadrilateral? |  |
| 3. What is the difference between a square and a rectangle? |  |
| 4. Can a quadrilateral have more than one pair of parallel sides? |  |
| 5. What is the significance of the diagonals in a quadrilateral? |  |

















