Shapes and Patterns NCERT Solutions | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
| Table of contents |

|
| Page No. 92-93 |

|
| Page No. 94-99 |

|
| Page No. 100 |

|
| Page No. 101 |

|
| Page No. 102 |

|
| Page No. 103 |

|
Page No. 92-93
Weaving Mats
You may have seen woven baskets of different kinds. If you look closely, you will notice different weaving patterns on each basket.
We will try weaving some mats with paper strips.
Q1: Let us make paper mats.
You will need —A coloured paper (30 cm long and 20 cm wide) and eight paper strips of two different colours (3 cm wide and longer than 20 cm).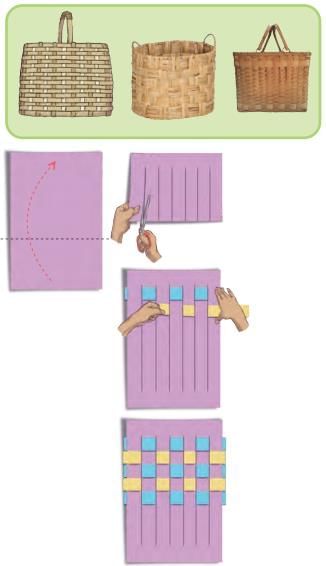 Ans:
Ans:
(a) Take a coloured paper 30 cm long and 20 cm wide.
(b) Fold the coloured paper in half along the longer side.
(c) Draw vertical lines at equal distances from the closed end and cut slits leaving a gap of 3 cm at the top.
(d) Carefully unfold the paper. There will be no cuts in the paper at the top and the bottom.
(e) Now cut 8 paper strips of 3 cm width in 2 colours and of length slightly longer than 20 cm.
(f) Take one colour strip and weave it across the slits going 1 under and 1 over, and again 1 under and 1 over. Repeat it for the first row.
(g) Take one more strip of another colour and weave it across the slits going 1 over and 1 under, and again 1 over and 1 under. Repeat it for the second row.
(h) Weave all the strips in the same alternating pattern. Neatly fold any extra strip ends behind the mat. Your mat is ready!
Q2: Can you figure out how to make this mat? Ans:
Ans:
Let us try to understand how this mat is woven by looking at the pattern in the first two rows.
Row 1 —2 over, 1 under, 2 over, 1 under, …
Row 2 —2 under, 1 over, 2 under, 1 over, …
You can use strips of the same colour or 2 different colours, one for each row.
Q3: Try to weave a pattern, using the rules given below Ans:
Ans:
Row 1 —2 over, 1 under, 2 over, 1 under, … (repeat).
Row 2 —1 under (do not repeat), 3 over, 3 under, 3 over, 3 under, … (repeat).
Row 3 —2 under, 1 over, 2 under, … (repeat).
Row 4—1 over (do not repeat), 3 under, 3 over … (repeat). Continue weaving in this order.
Q4: Can you work out the steps for any of these designs and weave the pattern?
Write the steps of the pattern in your notebook for each row until it starts repeating.
Ans:
For Image 1:
Row 1: 1 under (do not repeat), 3 over, 3 under, 3 over, … (repeat).
Row 2: 3 over, 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 3: 2 over (do not repeat), 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 4: 2 under (do not repeat), 3 over, 3 under, 3 over, … (repeat).
Row 5: 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 6:1 over (do not repeat), 3 under, 3 over, 3 under, … (repeat).
For Image 2:
Row 1: 1 under, 3 over, 1 under, 3 over, 1 under, … (repeat).
Row 2: 2 under (do not repeat), 1 over, 3 under, 1 over, 3 under, 1 over, … (repeat).
Row 3: 1 over, 3 under, 1 over, 3 under, 1 over, … (repeat).
Row 4: 2 over (do not repeat), 1 under, 3 over, 1 under, … (repeat).
Row 5: 1 under, 3 over, 1 under, 3 over, 1 under, … (repeat).
Row 6: 2 under (do not repeat), 1 over, 3 under, 1 over, 3 under, … (repeat)
Let Us Try
Draw the following pattern on a grid paper. Part of it is done for you.
Now, complete the rest of the grid to get the full design.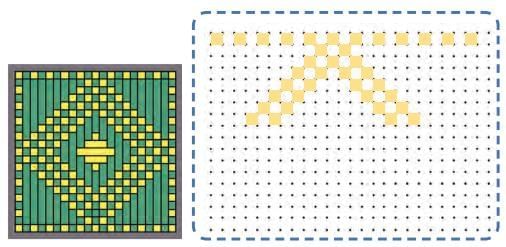 Ans:
Ans:
Do it yourself.
Page No. 94-99
Find Out
Q: Can five squares fit together around a point without any gaps or overlaps? Why or why not?
Ans:
No, five square cannot fit together perfectly around a point without any gaps or overlaps. Because, each angle of a square is a right angle. For shapes to fit perfectly around a point without gaps or overlaps (i.e., to form a tessellation around that point), the sum of the angles of the shapes meeting at that point must exactly equal to 4 right angles.
If we place five squares around a point, the sum of their angles would be 5 right angles which is greater than 4 right angles, so the squares would overlap.
Q: Can regular hexagons (6-sided shapes with equal sides) fit together around a point without any gaps or overlaps? Try and see (a sample hexagon is given at the end of the book). How many fit together at a point? Ans:
Ans:
Yes, regular hexagons can fit together around a point without any gaps or overlaps. Three hexagon fit perfectly around one central point, like pieces of a puzzle. They touch each other neatly without any empty spaces in between, and they don’t pile up on top of each other.
Q: What shapes have been used in this pattern?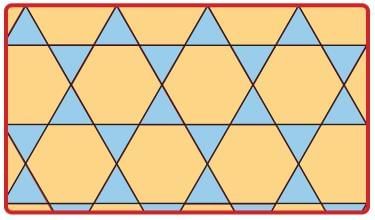 Ans:
Ans:
Equilateral triangles, Regular hexagons used in the above pattern.
Q: Continue the pattern given below and colour it appropriately.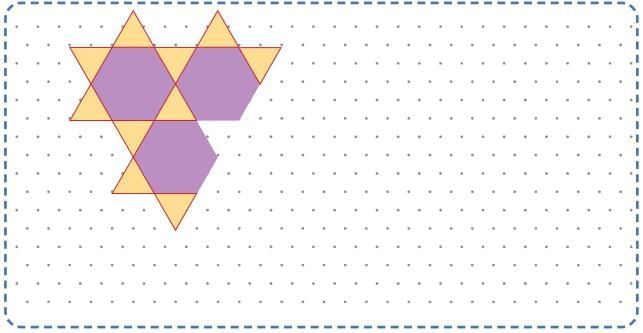 Ans:
Ans:
Do it yourself.
Q: Do regular octagons fit together without any gaps or overlaps?
Ans:
No, regular octagons do not fit together perfectly without any gaps or overlaps to form a tessellation.
Q: Look at the pattern given below. What shapes are coming together at the marked points? Are the same set of shapes coming together at these points? Continue the pattern and colour it appropriately.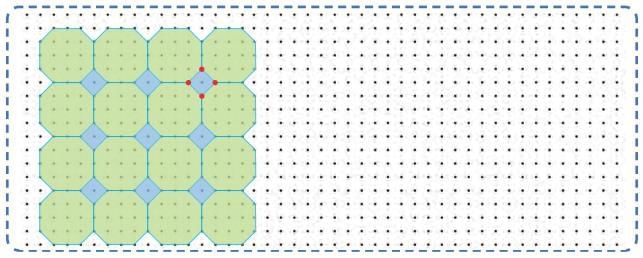 Ans:
Ans:
Shapes coming together at the marked points are square. Yes, same set of shapes are coming together at these points.
Q: Here is a tiling pattern made using two different shapes-squares and triangles. Are the triangles equilateral? Why or why not? Ans:
Ans:
Yes, as the sides of a square are equal, so the sides of triangles used to fill the gap must be of equal sides. So, the triangles are equilateral.
Q: What geometrical shapes can you make by fitting 2 of these triangles together? Trace the shapes you created.
Ans:
Do it yourself.
Q1: How many different types of triangles can you make?
Ans:
4, isosceles triangle, scalene triangle, equilateral triangle and right triangle.
Q2: Is it possible to make a triangle where all three sides are equal (equilateral triangle)?
Ans:
Yes, it is possible to make a triangle where all three sides are equal. Such a triangle is called an equilateral triangle.
Q3: Is it possible to make a triangle where all three sides are unequal?
Ans:
Yes, it is possible to make a triangle where all three sides are unequal. Such a triangle is called a scalene triangle.
Q4: How many different 4-sided shapes (quadrilaterals) can you make?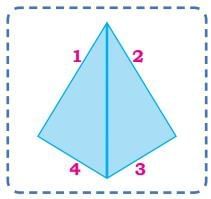 Here are three possible shapes.
Here are three possible shapes.
Have you made a shape like the one shown on the right?
Ans: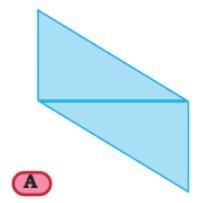
This shape is called a kite.
What do you notice about the sides of a kite?
Side 1 = Side 2.
Similarly, Side 3 = Side 4.
These sides are called adjacent sides.
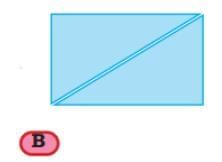
Here are two other possible quadrilaterals that are not kites.
Q5: Measure the sides of each of these two quadrilaterals A and B. What do you notice?
Are there any pairs of sides that are equal? Which pairs are equal—adjacent or opposite?
Ans:
Quadrilaterals whose opposite sides are equal are called parallelograms.
What types of angles do quadrilaterals A and B have? Which angles are equal in each of the above parallelograms?
In parallelogram A, opposite angles are equal.
In parallelogram B, all angles are equal and are right angles. Such a parallelogram is called a rectangle.
A rectangle is a special type of parallelogram.
Q6: In the grid given below, draw two different kites and parallelograms each.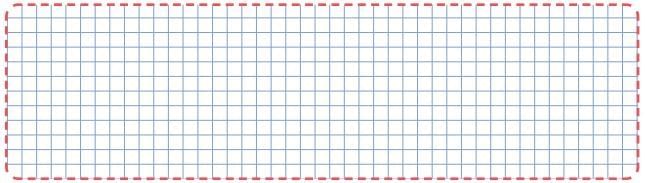 Ans:
Ans:
Do it yourself.
Q7: Now, use 3 triangles from the rhombus to form shapes. How many sides do each one of them have?
Using 3 triangular pieces of the rhombus, try creating a (a) 3-sided shape, (6) 4-sided shape, and (c) 5-sided shape.
Ans:
Do it yourself.
Q8: Which of these shapes can be made with all 4 pieces? Try and find out.
(a) Square
(b) Rectangle
(c) Triangle
(d) Pentagon (5-sided)
(e) Hexagon (6-sided)
(f) Octagon (8-sided)
Ans:
Do it yourself.
Tangram
Q: Look at the tangram set given at the end of your textbook. Cut out all the shapes. Name them.
(a) How are they same or different from each other?
(b) What do you notice about the angles of each of the shapes?
(c) What do you notice about the sides of each of the shapes? Ans:
Ans:
The given tangram consists of 7 pieces:
1. 2 large right triangles (the purple and the yellow)
2. 1 medium right triangle (orange)
3. 2 Small right triangles (the blue and the green)
4. 1 square (pink)
5. 1 parallelogram (the dark purple).
(a) They are same:
- All the shapes are flat (2D).
- All the shapes are polygons (made of straight lines).
- Other than the parallelogram, all the shapes have at least one right angle (all the triangles are right triangles, and the square has four right angles).
They are different:
- Number of sides and angles: The triangle have 3 sides and 3 angles.
- The square and the parallelogram each have 4 sides and 4 angles.
- Size: Tangram includes triangle of different sizes i.e., 2 large, 1 medium, 2 small.
(b) All the triangles: Each of the 5 triangles in the tangram set is a right-angled isosceles triangle.
- The square: All four angles are right angles.
- The parallelogram: It has two acute angles and two obtuse angles and opposite angles are equal.
(c) All the triangles: Since the triangle is an isosceles right angled triangle, so it has two equal sides and one longer side.
- The square: All four sides are equal in length.
- The parallelogram: It has two pairs of equal sides.
- Opposite sides are equal in length i.e., the two longer sides are equal, and the two shorter sides are equal.
Page No. 100
Which Shape Am I?
Q: Match the statements with appropriate shapes. Do some of them describe more than one shape?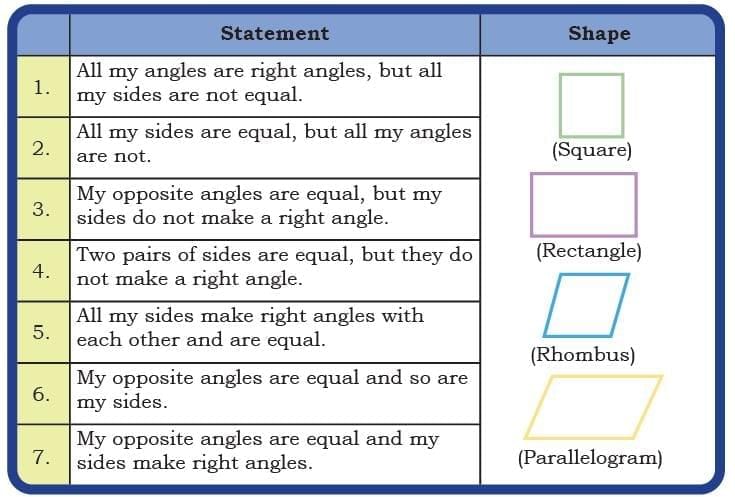 Ans:
Ans: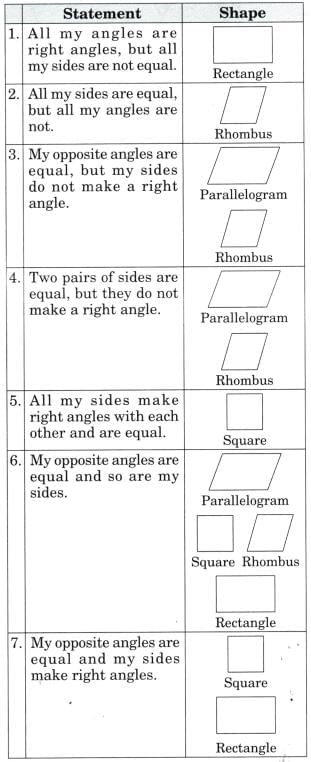
Kites
Make your own kite shape.
(a) Start with a square piece of paper.
(b) Take one corner of the paper and fold it towards the opposite corner, creating a sharp crease along the diagonal.
(c) Open and fold the corner A inwards, aligning the edge with the crease you just made.
(d) Repeat on the other side, folding the other corner B inwards to align with the crease at the centre.
You have a kite shape!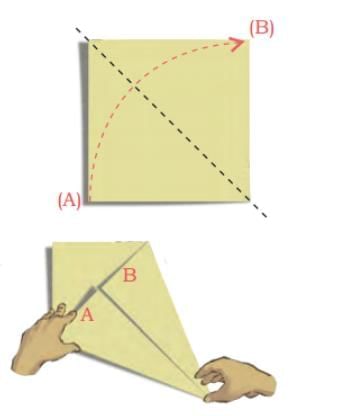 Q: What shapes do you see in the kite?
Q: What shapes do you see in the kite?
Ans:
Three right-angled triangle in which two are of same size.
Page No. 101
Circle Designs
Q: Can you think of a way to make a design exactly like the image given here? Try to make it.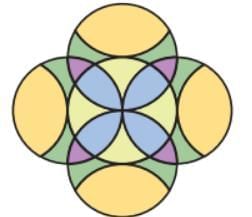 Ans:
Ans:
Do it yourself.
Page No. 102
Cube Connections
Q1: Here are three views of a cube. Can you draw them on the net in the correct order?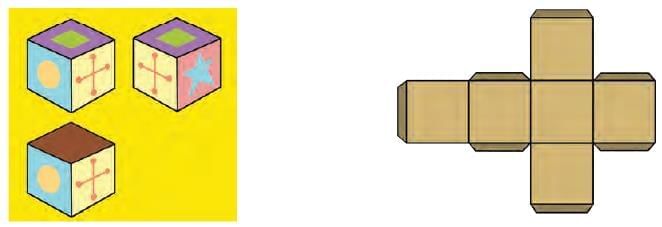 Ans:
Ans: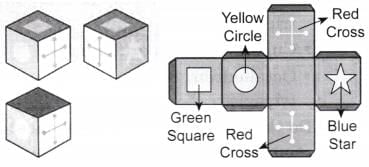
Q2: Here are some big solid cube frames. Howr many small cubes have been removed from each cube?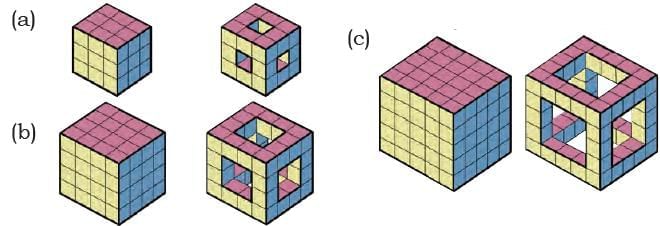
Ans:
(a) The full cube has 3 × 3 × 3 = 27 small cubes.
After removing the small cubes only the big cube frame are available, which has 20 small cubes.
So, total removed cubes = 27-20
= 7 cubes.
(b) The full cube has 4 × 4 × 4 = 64 small cubes.
After removing the small cubes the big cube frame has 32 small cubes.
So, total removed cubes = 64 – 32
= 32 cubes.
(c) The full cube has 5 × 5 × 5 = 125 small cubes.
After removing the small cubes the big cube frame has 44 small cubes.
So, total removed cubes = 125 – 44
= 81 cubes.
Q3: Nisha has glued 27 small cubes together to make a large solid cube. She paints the large cube red. How many of the original small cubes have—
(a) three faces painted red?
(b) two faces painted red?
(c) one face painted red?
(d) no faces painted red?
Ans:
Nisha has a large solid cube made from 27 small cubes. Since 3 × 3 × 3 = 27, the large cube is a 3 × 3 × 3 cube.
She paints the entire large cube red.
(a) The large solid cube has 8 corners small cubes, and each corner small cube is painted red.
So, 8 small cubes are three faces painted red.
(b) Since a cube has 12 edges or sides, and 1 cube in the middle of each edge is painted red.
So, there are 12 small cubes with two faces painted red.
(c) These are the small cubes located in the center of each face of the large cube. A cube has 6 faces. Each face of the large cube is a 3 × 3 square of small cubes. The center small cube of each 3 × 3 face has only one face exposed to the outside, or painted red. So, there are 6 small cubes with one face red.
(d) For a 3 × 3 × 3 = 27 cube, if we remove the outer layer of cubes, we are left with an inner cube. This means there is only 1 small cube right in the very center of the large cube that has no faces painted red.
Puzzle
Tanu arranged 7 shapes in a line. She used 2 squares, 2 triangles, 1 circle, 1 hexagon, and 1 rectangle.
Find her arrangement using the following clues:
(a) The square is between the circle and the rectangle.
(b) The rectangle is between the square and the triangle.
(c) The two triangles are next to the square.
(d) The hexagon is to the right of the triangle
(e) The circle is to the left of the square.
Ans:
The arrangement is: Triangle, Circle, Square, Rectangle, Triangle, Hexagon.
Page No. 103
Icosahedron and Dodecahedron
Q: What shapes do you see in an icosahedron and a dodecahedron?
Ans:
Icosahedron: Equilateral triangles, Dodecahedron: Regular pentagons
Q: Do all the faces look the same?
Ans:
Icosahedron: Yes, Dodecahedron: Yes
Q: How many faces meet at a vertex (point)?
Ans:
Icosahedron: 5 faces (Equilateral triangles), Dodecahedron: 3 faces (Regular pentagons)
Q: Do the same number of faces meet at each vertex?
Ans:
Icosahedron: Yes, Dodecahedron: Yes
Q: How many edges do you see?
Ans:
Icosahedron: 30, Dodecahedron: 30
Q: How did you count them such that you do not miss out any edge or count an edge twice?
Ans:
Do it yourself.
Q: Can you think of any other solid shapes that have faces that look the same?
Ans:
Yes, there are a few other types of shapes where all faces are identical. These are known as platonic solids. Besides the icosahedron and dodecahedron, the other platonic solids are:
- Tetrahedron: 4 faces, all are equilateral triangles.
- Cube: 6 faces, all are squares.
- Octahedron: 8 faces, all are equilateral triangles.
Do the same number of faces meet at each common vertex?
Ans:
Yes.
|
35 videos|322 docs|7 tests
|
FAQs on Shapes and Patterns NCERT Solutions - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are the different types of shapes and patterns that students learn in Class 5? |  |
| 2. How can patterns be identified in everyday life? |  |
| 3. Why is it important for students to learn about shapes and patterns? |  |
| 4. How can teachers effectively teach shapes and patterns to Class 5 students? |  |
| 5. What are some common challenges students face when learning about shapes and patterns? |  |



















