NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
Q.25. The partial pressure of ethane over a solution containing 6.56 × 10−3 g of ethane is 1 bar. If the solution contains 5.00 × 10−2 g of ethane, then what shall be the partial pressure of the gas?
Ans.
Molar mass of ethane (C2H6) = 2 × 12 + 6 × 1 = 30 g mol−1
Number of moles present in 6.56 × 10−2 g of ethane = 6.56 × 10-3 / 30
= 2.187 × 10−3 mol
Let the number of moles of the solvent be x.
According to Henry’s law,
p = KHx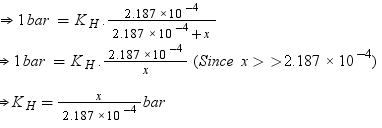
Number of moles present in 5.00 × 10−2 g of ethane = 5.00 × 10-2 /30 mol
= 1.67 × 10−3 mol
According to Henry’s law,
p = KHx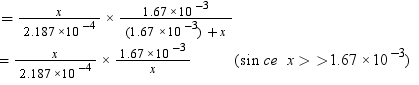
= 7.636 bar
Hence, partial pressure of the gas shall be 7.636 bar.
Q.26. What is meant by positive and negative deviations from Raoult's law and how is the sign of Δsol H related to positive and negative deviations from Raoult's law?
Ans. According to Raoult’s law, the partial vapour pressure of each volatile component in any solution is directly proportional to its mole fraction. The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The solutions that do not obey Raoult’s law (non-ideal solutions) have vapour pressures either higher or lower than that predicted by Raoult’s law. If the vapour pressure is higher, then the solution is said to exhibit positive deviation, and if it is lower, then the solution is said to exhibit negative deviation from Raoult’s law.
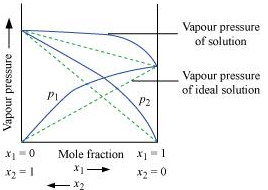
Vapour pressure of a two-component solution showing positive deviation from Raoult’s law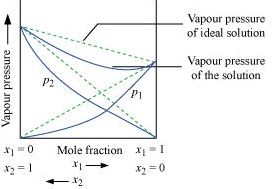
Vapour pressure of a two-component solution showing negative deviation from Raoult’s law
In the case of an ideal solution, the enthalpy of the mixing of the pure components for forming the solution is zero.
ΔsolH = 0
In the case of solutions showing positive deviations, absorption of heat takes place.
∴ ΔsolH = Positive
In the case of solutions showing negative deviations, evolution of heat takes place.
∴ ΔsolH = Negative
Q.27. An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
Ans. Here,
Vapour pressure of the solution at normal boiling point (p1) = 1.004 bar
Vapour pressure of pure water at normal boiling point (p°1) = 1.013 bar
Mass of solute, (w2) = 2 g
Mass of solvent (water), (w1) = 98 g
Molar mass of solvent (water), (M1) = 18 g mol−1
According to Raoult’s law,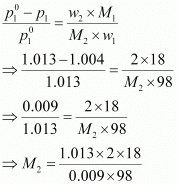
= 41.35 g mol−1
Hence, the molar mass of the solute is 41.35 g mol−1.
Q.28. Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure of a mixture of 26.0 g of heptane and 35 g of octane?
Ans. Vapour pressure of heptane (p°1) = 105.2 kPa
Vapour pressure of octane (p°2) = 46.8 kPa
We know that,
Molar mass of heptane (C7H16) = 7 × 12 + 16 × 1
= 100 g mol−1
Number of moles of heptane = 26 / 100 mol
= 0.26 mol
Molar mass of octane (C8H18) = 8 × 12 + 18 × 1
= 114 g mol−1
Number of moles of octane = 35/114 mol
= 0.31 mol
Mole fraction of heptane, x1 = 0.26 /(0.26 + 0.31)
= 0.456
And, mole fraction of octane, x2 = 1 − 0.456
= 0.544
Now, partial pressure of heptane, p1 = x1p10
= 0.456 × 105.2
= 47.97 kPa
Partial pressure of octane,
= 0.544 × 46.8
= 25.46 kPa
Hence, vapour pressure of solution, ptotal = p1 + p2
= 47.97 + 25.46
= 73.43 kPa
Q.29. The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
Ans. 1 molal solution means 1 mol of the solute is present in 1000 g of the solvent (water).
Molar mass of water = 18 g mol−1
Number of moles present in 1000 g of water = 1000/18
= 55.56 mol
Therefore, mole fraction of the solute in the solution is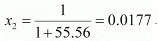
It is given that,
Vapour pressure of water, p°1 = 12.3 kPa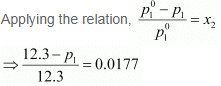
⇒ 12.3 − p1 = 0.2177
⇒ p1 = 12.0823
= 12.08 kPa (approximately)
Hence, the vapour pressure of the solution is 12.08 kPa.
Q.30. Calculate the mass of a non-volatile solute (molar mass 40 g mol−1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
Ans. Let the vapour pressure of pure octane be p°1
Then, the vapour pressure of the octane after dissolving the non-volatile solute is 80/100 p°1 = 0.8 p°1.
Molar mass of solute, M2 = 40 g mol−1
Mass of octane, w1 = 114 g
Molar mass of octane, (C8H18), M1 = 8 × 12 + 18 × 1
= 114 g mol−1
Applying the relation,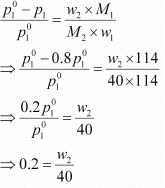
⇒ w2 = 8 g
Hence, the required mass of the solute is 8 g.
Q.31. A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further, 18 g of water is then added to the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate:
(i) molar mass of the solute
(ii) vapour pressure of water at 298 K.
Ans.
(i) Let, the molar mass of the solute be M g mol−1
Now, the no. of moles of solvent (water), 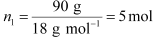
And, the no. of moles of solute, 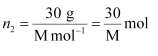
p1 = 2.8kPa
Applying the relation:
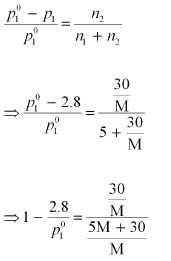
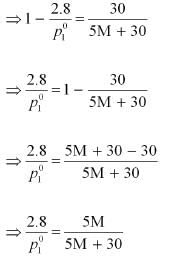
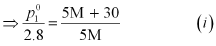
After the addition of 18 g of water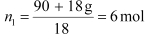
p1 = 2.9kPa
Again, applying the relation: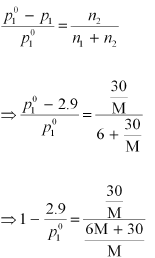
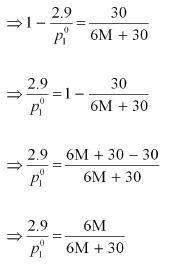
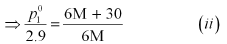
Dividing equation (i) by (ii), we have: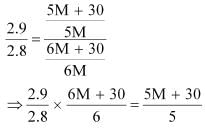
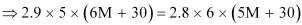
⇒ 87 M + 435 = 84 M + 504
⇒ 3 M = 69
⇒ M = 23 u
Therefore, the molar mass of the solute is 23 g mol−1.
(ii) Putting the value of ‘M’ in equation (i), we have: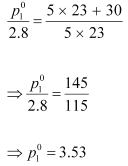
Hence, the vapour pressure of water at 298 K is 3.53 kPa.
Q.32. A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.
Ans.
 Fig: Structure of sugarcane
Fig: Structure of sugarcane
Here, ΔTf = (273.15 − 271) K = 2.15 K
Molar mass of sugar (C12H22O11) = 12 × 12 + 22 × 1 + 11 × 16 = 342 g mol−1
5% solution (by mass) of cane sugar in water means 5 g of cane sugar is present in (100 − 5)g = 95 g of water.
Now, number of moles of cane sugar = 5 / 342 mol = 0.0146 mol
Therefore, molality of the solution, m = 0.0146 mol / 0.095 kg = 0.1537 mol kg−1
Applying the relation,
ΔTf = Kf × m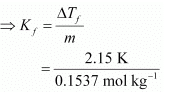
= 13.99 K kg mol−1
Molar of glucose (C6H12O6) = 6 × 12 + 12 × 1 + 6 × 16 = 180 g mol−1
5% glucose in water means 5 g of glucose is present in (100 − 5) g = 95 g of water.
Number of moles of glucose = 5 / 180 mol = 0.0278 mol
Therefore, molality of the solution, m = 0.0278 mol / 0.095 kg = 0.2926 mol kg−1
Applying the relation,
ΔTf = Kf × m
= 13.99 K kg mol−1 × 0.2926 mol kg−1
= 4.09 K (approximately)
Hence, the freezing point of 5% glucose solution is (273.15 − 4.09) K= 269.06 K.
Q.33. Two elements A and B form compounds having formula AB2 and AB4. When dissolved in 20 g of benzene (C6H6), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 Kkg mol−1. Calculate atomic masses of A and B.
Ans. We know that,
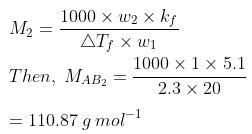
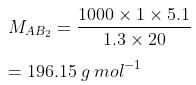
Now, we have the molar masses of AB2 and AB4 as 110.87 g mol−1 and 196.15 g mol−1 respectively.
Let the atomic masses of A and B be x and y respectively.
Now, we can write
x + 2y = 110.81 .... (1)
x + 4y = 196.15 .... (2)
Subtracting equation (i) from (ii), we have
2y = 85.28
⇒ y = 42.64
Putting the value of ‘y’ in equation (1), we have
x + 2 × 42.64 = 110.87
⇒ x = 25.59
Hence, the atomic masses of A and B are 25.59 u and 42.64 u respectively.
Q.34. At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?
Ans. Here,
T = 300 K
π = 1.52 bar
R = 0.083 bar L K−1 mol−1
Applying the relation,
π = CRT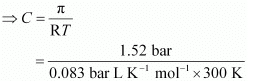
= 0.061 mol
Since the volume of the solution is 1 L, the concentration of the solution would be 0.061 M.
|
334 videos|660 docs|300 tests
|
FAQs on NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
| 1. What are the NCERT Solutions? |  |
| 2. Why are NCERT Solutions important for exam preparation? |  |
| 3. How can I access NCERT Solutions for my exams? |  |
| 4. Are NCERT Solutions enough for exam preparation? |  |
| 5. How can NCERT Solutions help me score better in exams? |  |





















