NCERT Solutions for Class 10 Maths Chapter 14 - Probability (Exercise 14.1) - 1
Exercise 14.1
Q1. Complete the following statements.
(i) Probability of an event E + Probability of the event ‘not E’ = ________
(ii) The probability of an event that cannot happen is ________. Such an event is called ________.
(iii) The probability of an event that is certain to happen is ________ Such an event is called ________.
(iv) The sum of the probabilities of all the elementary events of an experiment is ________.
(v) The probability of an event is greater than or equal to ________ and less than or equal to ________.
Ans:
(i) Probability of an event E + Probability of the event 'not E' = 1.
(ii) The probability of an event that cannot happen is 0. Such an event is called an impossible event.
(iii) The probability of an event that is certain to happen is 1. Such an event is called a sure or certain event.
(iv) The sum of the probabilities of all the elementary events of an experiment is 1.
(v) The probability of an event is greater than or equal to 0 and less than or equal to 1.
Q2. Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
Ans:
(i) Since the car may or may not start, thus the outcomes are not equally likely.
(ii) The player may shoot or miss the shot.
∴ The outcomes are not equally likely.
(iii) In advance, it is known that the answer is to be either right or wrong.
∴ The outcomes right or wrong are equally likely to occur.
(iv) In advance, it is known the newly born baby has to be either a boy or a girl.
∴ The outcomes, either a boy or a girl are equally likely to occur.
Q3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
Ans: Since on tossing a coin, the outcomes ‘head’ and ‘tail’ are equally likely, the result of tossing a coin is completely unpredictable and so it is a fairway.
Q4. Which of the following cannot be the probability of an event?
(a) 2/3
(b) − 1.5
(c) 15%
(d) 0.7
Ans: (b)
Solution: Since the probability of an event cannot be negative.
∴ Option (b) −1.5 cannot be the probability of an event.
Q5. If P(E) = 0.05, what is the probability of ‘not E’?
Ans: We know that,
P(E) + P(not E) = 1
∴ 0.05 + P(not E) = 1 ⇒ P(not E) = 1 − 0.05
= 0.95
Thus, the probability of ‘not E’ = 0.95.
Q6. A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Ans:
(i) Since, there are lemon flavoured candies only in the bag,
∴ Taking out any orange flavoured candy is not possible.
⇒ Probability of taking out an orange flavoured candy = 0.
(ii) Also, the probability of taking out a lemon flavoured candy = 1.
Q7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Ans: ∴ Let the probability of 2 students having same birthday = P(SB) And the probability of 2 students not having the same birthday = P(nSB)
∴ P(SB) + P(nSB)=1
⇒ P(SB) + 0.992 = 1
⇒ P(SB)=1 − 0.992 = 0.008
So, the required probability of 2 boys having the same birthday = 0.008.
Q8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red? (ii) not red?
Ans:
Total number of balls = 3 + 5 = 8
∴ Number of all possible outcomes = 8
(i) For red balls
There are 3 red balls.
∴ Number of favourable outcomes = 3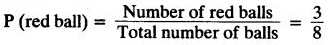
(ii) For not red balls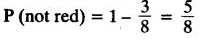
Q9. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red? and (ii) white? (iii) not green?
Ans:
Total number of marbles = 5 + 8 + 4 = 17
(i) For red marbles
∵ Number of red marbles = 5
∴ Number of favourable outcomes = 5
∴ Probability of red marbles, P(red) = 5/17
(ii) For white balls
∵ Number of white balls = 8
∴ Probability of white balls,
∴ P(white)= 8/17
(iii) For not green balls
∵ Number of white balls = 4
∴ Number of ‘not green’ balls = 17 − 4 = 13
i.e., Favourable outcomes = 13
P(not green) = 13/17
OR
Number of green marbles = 4
∴ Number of ‘not green balls’ = 17 − 4 = 13
⇒ Favourable outcomes = 13
∴ P(not green) = 13/17
Q10. A piggy bank contains hundred 50p coins, fifty Rs 1 coins, twenty Rs 2 coins and ten Rs 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin (i) will be a 50p coin? and (ii) will not be Rs 5 coin?
Ans:
Number of:
50 p coins = 100
Re 1 coins = 50
Rs 2 coins = 20
Rs 5 coins = 10
Total number of coins = 100 + 50 + 20 + 10 = 180
(i) For a 50 p coin:
Favourable events = 100
∴ P(50 p) = 100/180 = 5/9
(ii) For not a Rs 5 coin:
a Number of Rs 5 coins = 10
∴ Number of ‘not Rs 5’ coins = 180 − 10 = 170
⇒ Favourable outcomes = 170
∴ P(not 5 rupee coin) = 170/180 = 17/18.
Q11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig.). What is the probability that the fish taken out is a male fish?

Ans:
Number of:
Male fishes = 5
Female fishes = 8
∴ Total number of fishes = 5 + 8 = 13
⇒ Total number of outcomes = 13
For a male fish:
Number of favourable outcomes = 5
∴ P(male fish) = 5/13.
Q12. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure), and these are equally likely outcomes. What is the probability that it will point at
(i) 8?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
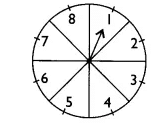 Ans: Total numbers marked = 8
Ans: Total numbers marked = 8
(i) When pointer points at 8
Total number of outcomes = 8
Number of favourable outcomes = 1
∴ P(8)
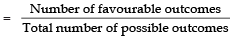
= 1/8
(ii) When pointer points at an odd number
Number of odd numbers from 1 to 8 = 4
[∵ Odd numbers are 1, 3, 5 and 7]
⇒ Number of favourable outcomes = 4
∴ P(odd) = 
(iii) When pointer points at a number greater than 2
Number of numbers greater than 2 = 6
[∴ The numbers 3, 4, 5, 6, 7 and 8 are greater than 2]
⇒ Number of favourable outcomes = 6
∴ P(greater than 2) = 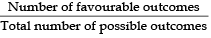
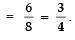
(iv) When pointer points a number less than 9:
Number of numbers less than 9 = 8
[a The numbers 1, 2, 3, 4, 5, 6, 7 and 8 are less than 9]
∴ Number of favourable outcomes = 8
P(greater than 9)

Q13. A die is thrown once. Find the probability of getting
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number.
Ans: Since, numbers on a die are 1, 2, 3, 4, 5, and 6.
∴ Number of total outcomes = 6
(i) For prime numbers
Since 2, 3, and 5 are prime numbers,
∴ Favourable outcomes = 3
P(prime) =
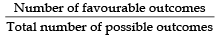
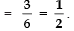
(ii) For a number lying between 2 and 6
Since the numbers between 2 and 6 are 3, 4 and 5
∴ Favourable outcomes = 3
(iii) For an odd number
Since 1, 3 and 5 are odd numbers.
⇒ Favourable outcomes = 3
Q14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Ans: Number of cards in deck = 52
∴ Total number of possible outcomes = 52
(i) For a king of red colour
∵ Number of red colour kings = 2
[∵ Kings of diamond and heart are red]
∴ Number of favourable outcomes = 2
E(red king)
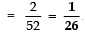
(ii) For a face card
∵ 4 kings, 4 queens and 4 jacks are face cards
∴ Number of face cards = 12
⇒ Number of favourable outcomes = 12
∴ P(face)
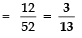
(iii) For a red face card
Since cards of diamond and heart are red
∴ There are [2 kings, 2 queens, 2 jacks] 6 cards are red
⇒ Favourable outcomes = 6
∴ P(red face)
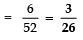
(iv) For a jack of hearts
Since there is only 1 jack of hearts.
∴ Number of favourable outcomes = 1
P(jack of hearts)
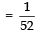
(v) For a spade
∵There are 13 spades in a pack of 52 cards:
∴ Favourable outcomes are 13.
P(spade)
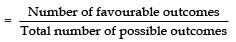
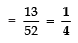
(vi) For the queen of diamonds
∵ There is only one queen of a diamond.
∴ Number of favourable outcomes = 1
P(queen of diamonds)
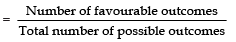
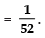
Q 15: Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? and (b) a queen?
Sol: We have five cards.
∴ All possible outcomes = 5
(i) For a queen:
∵ Number of queens = 1
(ii) The queen is drawn and put aside,
∴ Only 5 − 1 = 4 cards are left,
⇒ All possible outcomes = 4
(a) For an ace:
∵ There is only one ace
∴ Number favourable outcomes = 1
(b) For a queen:
Since, the only queen has already been put aside.
∴ Number of possible outcomes = 0
Q 16: 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Sol: We have
Number of good pens = 132
Number of defective pens = 1 2
∴ Total number of pens = 132 + 12 = 144
For good pens:
∵ There are 132 good pens
∴ Number of favourable outcomes = 132
Q 17: (i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Sol: Since, there are 20 bulbs in the lot.
∴ Total number of possible outcomes = 20
(i) ∵ Number defective bulbs = 4
i.e., Favourable outcomes = 4
(ii) ∵ The bulb drawn above is not included in the lot.
∴ Remaining number of bulbs = 20 − 1 = 19.
⇒ Total number of possible outcomes = 19.
∵ Number of bulbs which are not defective = 19 − 4 = 15
⇒ Favourable number of outcomes = 15
Q 18: A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears (i) a two-digit number, (ii) a perfect square number and (iii) a number divisible by 5.
Sol: We have:
Total number of discs = 90
∴ Total number of possible outcomes = 90
(i) For a two-digit number:
Since the two-digit numbers are 10, 11, 12, ....., 90.
∴ Number of two-digit numbers = 90 − 9 = 81
[∵ 1, 2, 3, 4, 5, 6, 7, 8, and 9 are 1-digit numbers]
⇒ Number of favourable outcomes = 81
(ii) For a perfect square:
Perfect squares from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, and 81
∴ Number of perfect numbers = 9
⇒ Number of favourable outcomes = 9
(iii) For a number divisible by 5:
Numbers divisible by 5 [from 1 to 90] are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90
i.e. There are 18 number (1 to 90) which are divisible by 5.
∴ Number of favourable outcomes = 18
Q 19: A child has a die whose six faces show the letters as given below:
The die is thrown once. What is the probability of getting (i) A? and (ii) D?
Sol: Since there are six faces of the given die and these faces are marked with letters
∴ Total number of letters = 6
⇒ Number of possible outcomes = 6
(i) For the letter A
∵ Two faces are having the letter A.
∴ Number of favourable outcomes = 2
(ii) For the letter D:
∵ Number of D’s = 1
∴ Number of possible outcomes = 1
Q 20: Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 1 m?
Sol: Here, Area of the rectangle = 3 m × 2 m = 6 m2
And, the area of the circle = πr2
∴ Probability for the die to fall inside the circle
Q 21: A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that (i) She will buy it? (ii) She will not buy it?
Sol: Total number of ball pens = 144
⇒ All possible outcomes = 144
(i) Since there are 20 defective pens
∴ Number of good pens 144 − 20 = 124
⇒ Number of favourable outcomes = 124
∴ Probability that she will buy it
(ii) Probability that she will not buy it
=1 − [Probability that she will buy it]
Q 22: Two dice one blue and one grey, are thrown at the same time. Now Complete the following table:
(ii) A student argues that there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability 1/11. Do you agree with this argument? Justify your answer.
Sol:
∵ The two dice are thrown together.
∴ Following are the possible outcomes:
(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6).
(2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6).
(3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6).
(4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6).
(5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6).
(6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6).
⇒ Number of all possible outcomes is 6 × 6 = 36.
(i) Let the required probability be P(E).
(a) ∵ The sum on two dice is 3 for: (1, 2) and (2, 1)
∴ Favourable outcomes = 2
(b) a The sum on two dice is 4 for: (1, 3), (2, 2) and (3, 1).
∴ Number of favourable outcomes = 3
(c) ∵ The sum on two dice is 5 for:
(1, 4), (2, 3), (3, 2) and (4, 1)
∴ Number of favourable outcomes = 4
(d) The sum on two dice is 6 for:
(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)
∴ Number favourable outcomes = 5
(e) The sum on two dice is 7 for:
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) and (6, 1)
∴ Number of favourable outcomes = 6
(f) The sum on two dice is 9 for:
(3, 6), (4, 5), (5, 4) and (6, 3)
∴ Number of favourable outcome = 4
(g) The sum on two dice is 10 for:
(4, 6), (5, 5), (6, 4)
∴ Number of favourable outcomes = 3
(h) The sum on two dice is 11 for:
(5, 6) and (6, 5)
∴ Number of favourable outcomes = 2
Thus, the complete table is as under: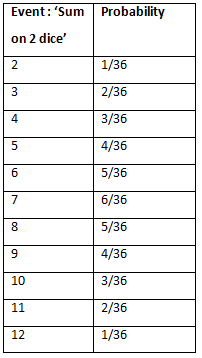
(ii) No. The number of all possible outcomes is 36 and not 11.
∴ The argument is not correct.
Q 23: A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Sol: Let T denotes the tail and H denotes the head.
∴ All the possible outcomes are:
HHH, HHT, HTT, TTT, TTH, THT, TTH, HTH
∴ Number of all possible outcomes = 8
Let the event that Hanif will lose the game be denoted by E.
∴ Favourable events are:
HHT, HTH, THH, THT , TTH, HTT
⇒ Number of favourable outcomes = 6
Q 24: A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Sol: Since, throwing a die twice or throwing two dice simultaneously is the same.
∴ All possible outcomes are:
(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6)
(2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6)
(3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6)
(4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6)
(5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6)
(6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)
∴ All possible outcomes = 36
(i) Let E be the event that 5 does not come up either time, then The favourable outcomes are [36 − (5 + 6)] = 25
The favourable outcomes are [36 − (5 + 6)] = 25
(ii) Let N be the event that 5 will come up at least once, then Number of favourable outcomes = 5 + 6 = 11
Q 25: Which of the following arguments are correct and which are not correct? Give reasons for your answer. (i) If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is 1/3.
(ii) If a die is thrown, there are two possible outcomes—an odd number or an even number.
Therefore, the probability of getting an odd number is 1/2.
Sol: (i) Argument is incorrect.
The possible outcomes are- (HH), (HT), (TH), (TT)
∴ 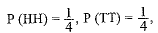
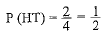
(ii) Argument is correct.
Possible outcomes = 1, 2, 3, 4, 5, 6
Odd numbers are = 1, 3, 5,
Hence P (an odd number) = 3/6 = 1/2
Even numbers are = 2, 4, 6,
Hence P (an even number) = 3/6 = 1/2
|
129 videos|736 docs|84 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 14 - Probability (Exercise 14.1) - 1
| 1. What is the basic concept of probability in Class 10? |  |
| 2. How do you calculate the probability of an event occurring? |  |
| 3. What is the difference between experimental probability and theoretical probability? |  |
| 4. Can you provide examples of simple probability experiments for Class 10 students? |  |
| 5. What are the common mistakes to avoid when solving probability problems in Class 10? |  |






















