NCERT Solutions for Class 5 Maths - Boxes and Sketches
| Table of contents |

|
| Page no. 126 |

|
| Page no. 127 |

|
| Page no. 128 |

|
| Page no. 129 |

|
| Page no. 130 |

|
| Page no. 132 |

|
| Page no. 133 |

|
Page no. 126
Sweet Box:
Ramya went to buy sweets. The shopkeeper took a paper cut-out and quickly made a lovely pink box for the sweets!

1. She made four more shapes. Each is to be folded along the dotted lines. You have to find out which of these can be made into a box.
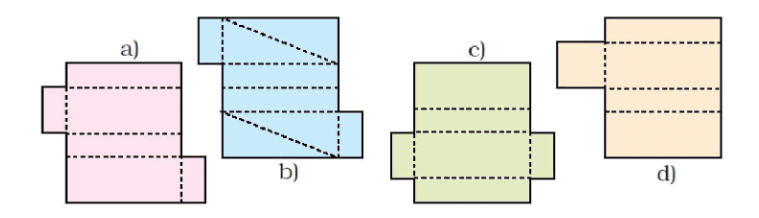
Ans: Cut outs (a) and (c) can be folded along the dotted lines to make a box.
Page no. 127
Shapes that Fold into a Cube
Buddha wants to make a paper cube using a squared sheet. He knows that all the faces of a cube are squares. He draws two different shapes.
1. Will both these shapes fold into a cube?
Ans: Yes, both shapes can be folded into cubes.
Each shape has six squares, and they are arranged in a valid layout that allows all the squares to fold into the six faces of a cube.
2. Draw at least one more shape which can fold into a cube.
Ans: 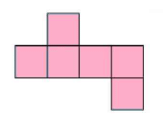
The figure consists of six squares arranged in such a way that it can be folded into a cube.
3. What will be the area of each face of the cube?
Ans: The area of each face of the cube = side × side.
4. Draw one shape which will not fold into a cube.
Ans: 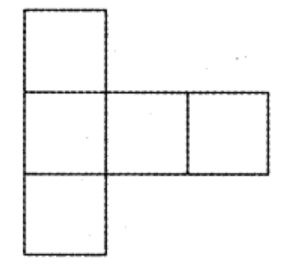
The shape shown in the image cannot fold into a cube. This is because, while it consists of five squares, the arrangement is such that when folded, some faces will overlap or leave gaps, preventing it from forming a proper 3D cube.
5. Look around and discuss which things around you look like a cube. List a few.
Ans: Following objects look like a cube:
Dice, chalk box, Rubik's Cube, etc.
Shapes for an Open Box:
Remember the puzzles with five squares in chapter 3? You saw 12 different shapes made with five squares (page 46).
If you cut those shapes and fold them, some of those will fold into an open box (box without a top).
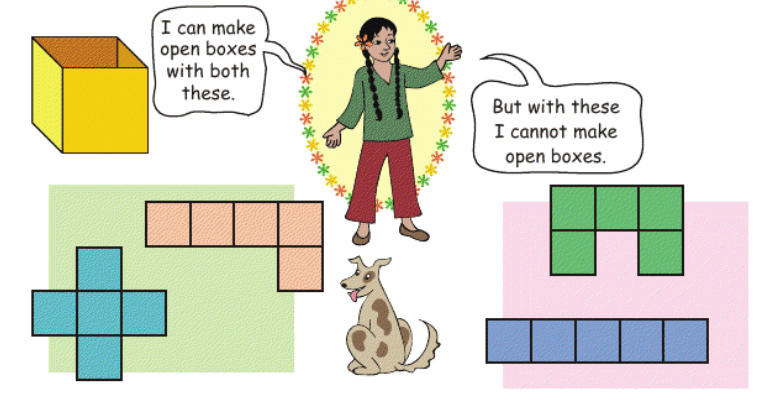
1. Find out which of the other 8 shapes (on page no. 46) can be folded
to make an open box.
Ans: 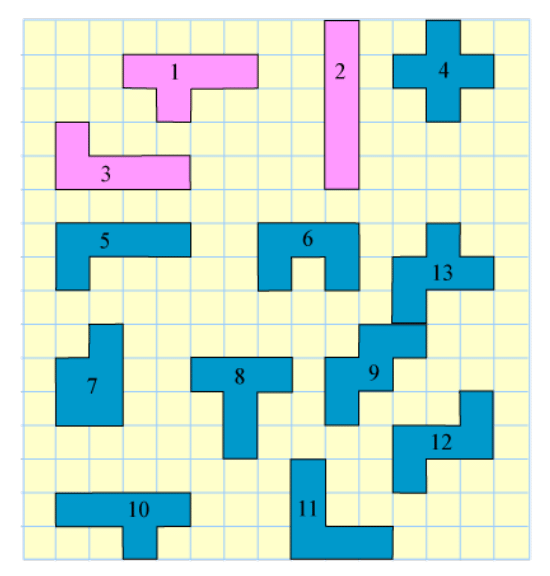
Out of these shapes, 1, 8, 9, 10, 12, and 13 can be folded into cubes.
A valid net for a cube allows each square to form one face of the cube.
The shapes mentioned (1, 8, 9, 10, 12, and 13) meet this criterion, and they can be folded to form an open or closed box (cube).
Therefore, these shapes can be folded into a cube.
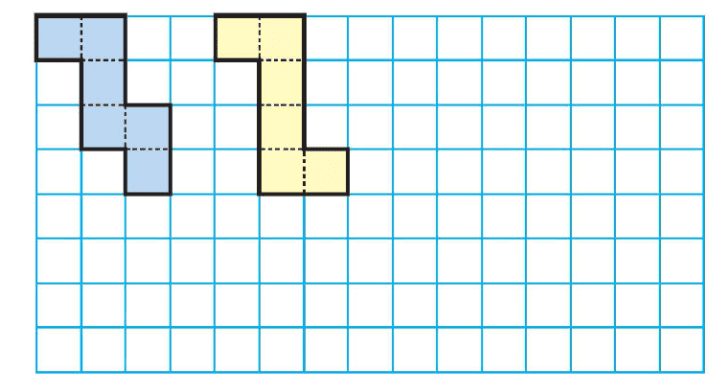
2. Draw more shapes which will not fold to make an open box.
Ans: 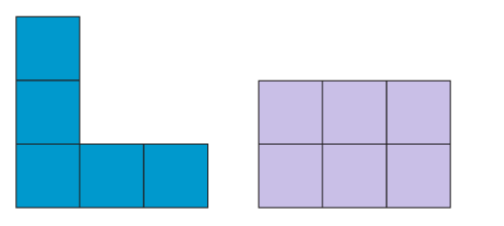
First Shape (Blue L-shaped):
This shape consists of five squares arranged in an "L" shape. Since it only has five squares, it cannot form a cube, which requires exactly six squares to cover all six faces of the cube. Even if a sixth square were added, this particular arrangement would not fold properly into a cube due to the way the squares are positioned.
Second Shape (Purple Grid):
This shape is a flat 2x3 grid of squares. Although it has six squares, which is the correct number for forming a cube, the arrangement of the squares is incorrect. When folded, some squares would overlap or leave gaps, preventing it from forming a proper 3D cube.
Conclusion:
These shapes cannot fold into a cube due to either insufficient squares or improper arrangement.
Page no. 128
Boxes and Boxes:
1. All boxes are not cubes. Here are some different kinds of boxes.
Match the shape on the left with a box into which it will fold.
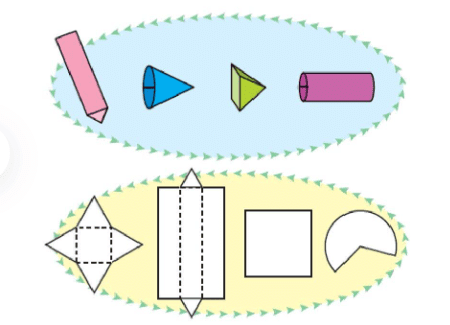
Ans: 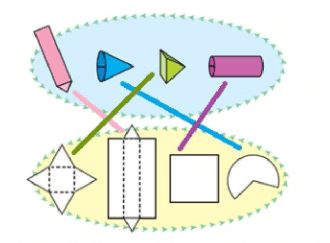
Page no. 129
Floor Maps:
1. For making a house a floor map is first made. Have you ever seen a floor map? Here is a floor map of Vibha’s house. It shows where the windows and the doors are in the house.
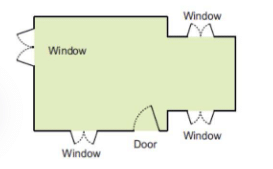
Ans: Yes, I have seen a floor map.
2. Which is the front side of her house? How many windows are there on the front side?
Ans: The side that contains the door is the front side. There are two windows on the front side.
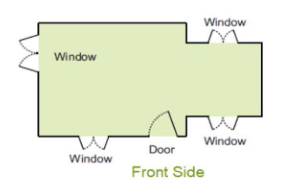
3. Which one is Vibha’s house?
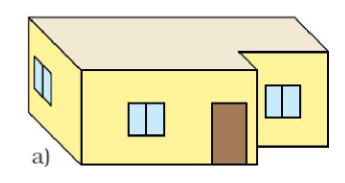
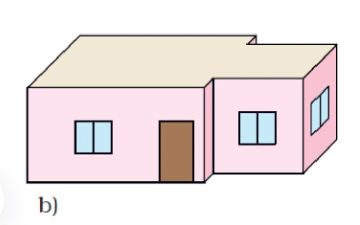
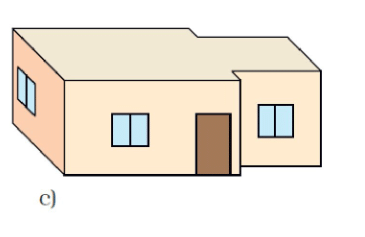
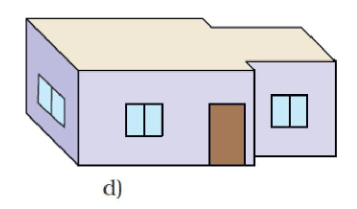
Ans: Deep Drawing d) is Vibha's house.
4. Why do the other three deep drawings not match the floor map? Discuss.
Ans: Drawing (a) shows a straight back wall. Thus, it does not match the floor map.
Drawing (b) shows a window on the right side. Thus, it does not match the floor map.
Drawing (c) shows all windows of equal size. Thus, it does not match the floor map.
Deep drawing (d) exactly matches the floor map. Thus, the answer is d).
Page no. 130
Practice Time:
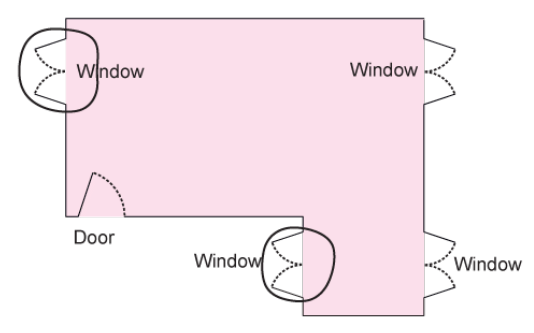
1. Look at this floor map of a house. Make doors and windows on the deep drawing of this house.
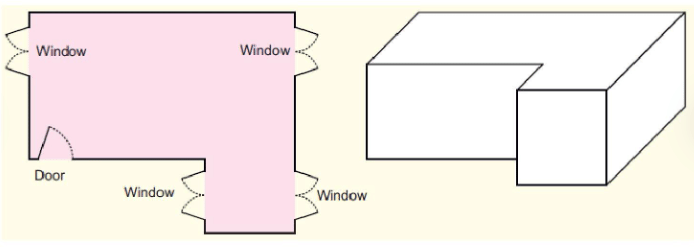
Ans: 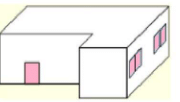
(i) Are there any windows you couldn’t show on the deep drawing?
Circle them on the floor map.
Ans: Yes, I couldn't show the following windows on my deep drawing.
A Deep Drawing of a Cube:
Soumitro and his friends made deep drawings of a cube. These are their drawings.
(a) Which of these drawing look correct to you?
Ans: The drawing numbered (d) and (e) look correct.
(b) Can you add some lines to make drawing (f) into a deep drawing of the cube?
Ans: Yes, I can add some lines to make drawing (f) into a deep drawing of the cube as shown.
Puzzle
1. This cut-out is folded to make a cube.
Which of these are the correct deep drawings of that cube?
Ans: (a), and (e) are the correct deep drawings of the cube made out of the given cut-out.
Option (a) and Option (e) correctly represent how the faces align after folding the cut-out into a cube. The positions of the dots on adjacent faces match the arrangement in the cut-out.
Option (b), Option (c), and Option (d) do not match the correct adjacent face arrangement and therefore cannot be the correct representations.
A Simple Way to Draw a Cube:
Chanda wants to make a deep drawing of this cube. She draws the cube like
this.


1. In the same way make a deep drawing of a box which looks like this.

Ans: 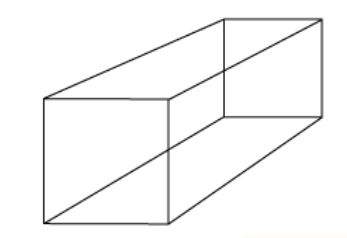
Page no. 132
Matchbox Play:
Navin, Bhaskar and Pratigya made this bridge using matchboxes.

Navin and Pratigya made drawings of the bridge.
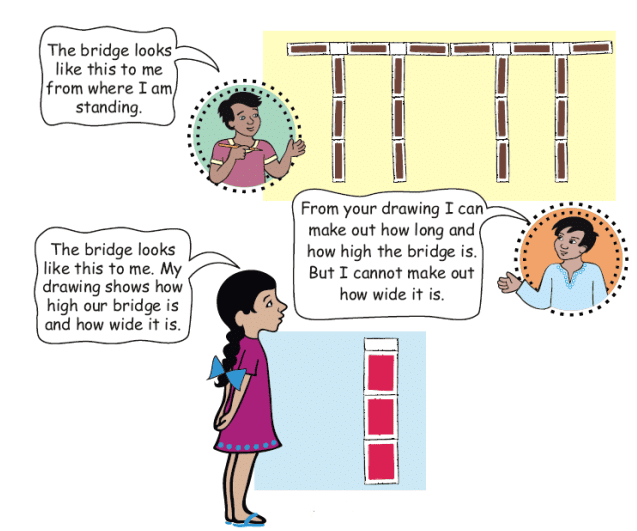
1. If you look at the bridge from the top, how will it look? Choose
the right drawing below:

Ans: 
2. Look at the photo and try to make a deep drawing of this bridge.
Ans: 
Page no. 133
Practice Time:
1. Make drawings to show how this bridge will look 
(a) From the top
Ans: 
(b) From the front
Ans: 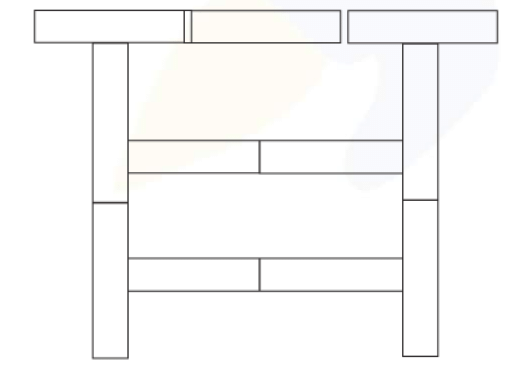
(c) From the side
Ans: 
2. Make a matchbox model which looks like this.

Also make a deep drawing of the model in your notebook.
Ans: 
Top View: The top view shows a grid of matchboxes arranged in a 3x2 layout.
Front View: The front view shows stacks of matchboxes arranged in different heights.
Side View: The side view shows the height differences in the model, with matchboxes stacked in two levels.
3. How many cubes are needed to make this interesting model?
The number of cubes in the top most row = 9
The number of cubes in the second row = 9 + 7 = 16
The number of cubes in the third row = 9 + 7 + 5 = 21
The number of cubes in the fourth row = 9 + 7 + 5 + 3 = 24
The number of cubes in the bottom row = 9 + 7 + 5 + 3 + 1 = 25
Total number of cubes = 9 + 16 + 21 + 24 + 25 = 95.
(a) Here are some drawings for the model. Mark the correct top view drawing with ‘T’ and the correct side view drawing with ‘S’.
Ans: 
Top View:
The top view of the model should display how the structure appears when viewed from directly above. This typically shows the layout of the structure in terms of space, but without any indication of height.
Option (d) is the correct top view because it shows the layout of the structure as seen from above.
Side View:
The side view represents the height and layering of the model. It will show the number of blocks stacked at each position when viewed from the side.
Option (b) is the correct side view, as it accurately represents the stepped stacking of the model.
Based on the analysis, the correct labels for the views are as follows:
T for (d)
S for (b).
|
31 videos|192 docs|41 tests
|
FAQs on NCERT Solutions for Class 5 Maths - Boxes and Sketches
| 1. What are the main concepts covered in the article "Boxes and Sketches"? |  |
| 2. How can I improve my skills in drawing boxes and sketches? |  |
| 3. What tools are recommended for creating boxes and sketches? |  |
| 4. Are there any tips for visualizing three-dimensional objects while sketching? |  |
| 5. How can boxes and sketches be applied in real-world scenarios? |  |





















