NCERT Solutions for Class 5 Maths - Can you See The Pattern
1. What should come next?
(a)

(b)

(c)

(d)

Ans.
(a)

Observe the partition line moving by 45°.
(b)

Observe the alternate pattern of the letters N and Z.
The first letter is N and then second letter is Z.
The letter N, then the letter Z. Again, the letter N, so what should come next is the letter Z.
(c)

Observe the single dot in the triangle, which is rotating in a clockwise direction.
First, it is at bottom of the triangle, then it moves to the left- hand side, and then to right side of triangle.
Following the clockwise direction, it moves to the bottom again and then to the left- hand side.
This cycle continues.
(d)

Observe the rotation which is inside the circle.
It is rotating by an angle of 90°.
2. See this pattern
(a) 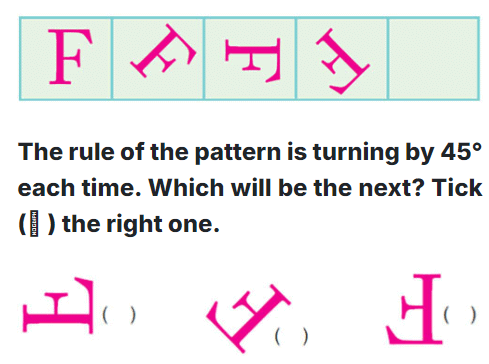
Ans:
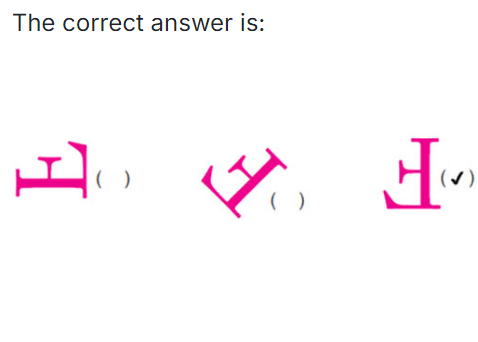
Using the same rule take it forward till you get back to what you started with.
(b) 
Ans: 
(c) 
Ans: 
3. Some patterns are given below on the left side of the red line.
For each pattern, write the rule. Then choose what comes
next from the right side of the line and tick (✔) it.
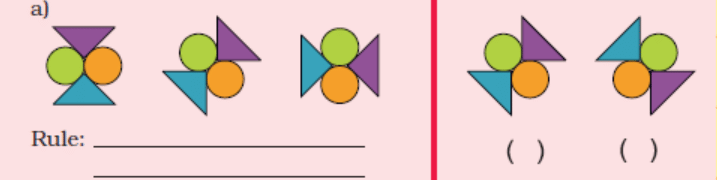
Ans : 
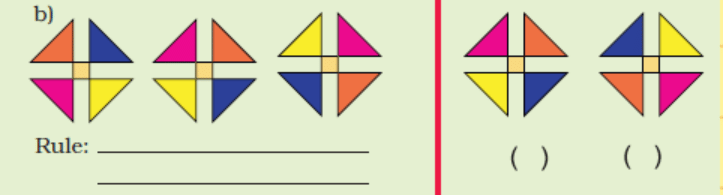
Ans: 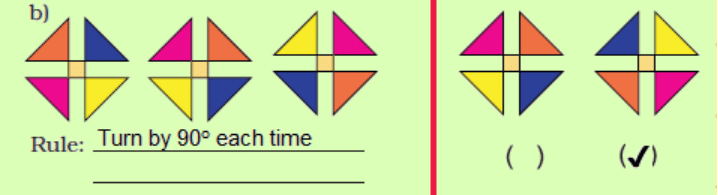
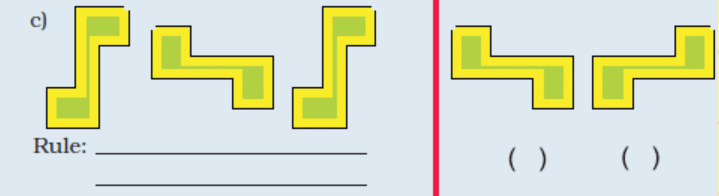
Ans: 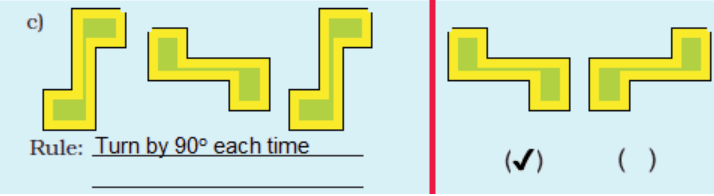

Ans: 
4. Look for a Pattern
Mark that picture which is breaking the rule. Also, correct it.

Ans: The picture marked below breaks the rule.
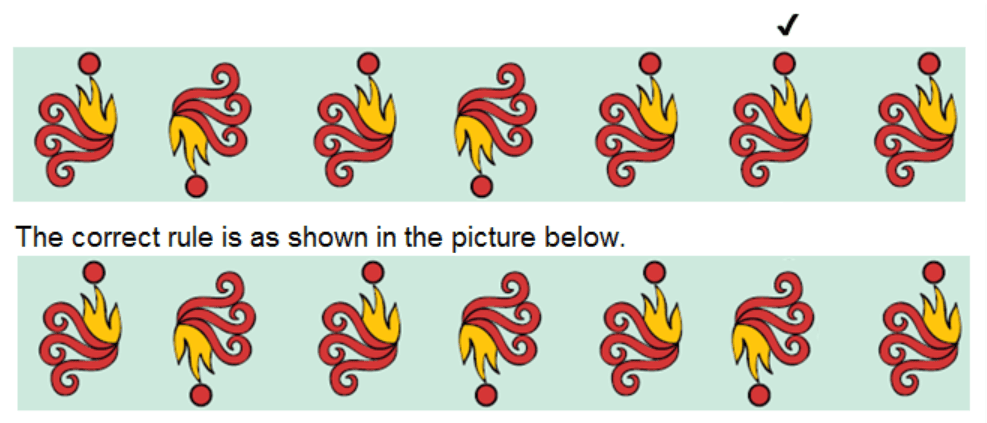
Observe the pattern of red dot.
It is moving up and down.

Ans: The picture marked below breaks the rule.
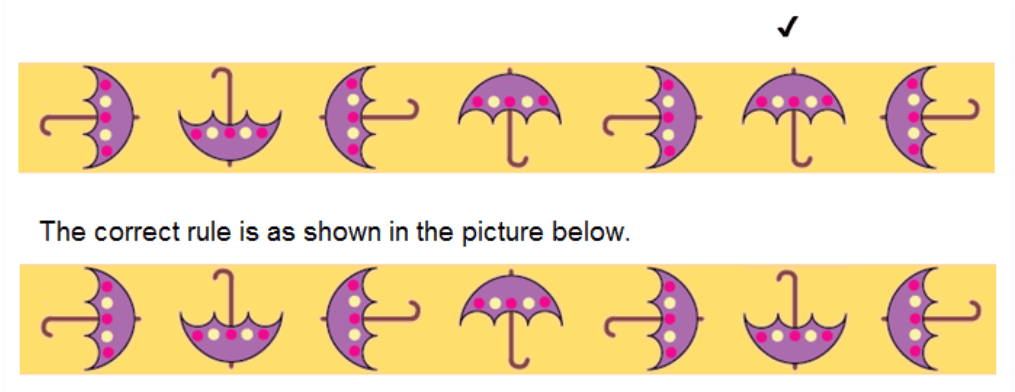
The umbrella is turned by 90°.
Ans: The picture marked below breaks the rule.

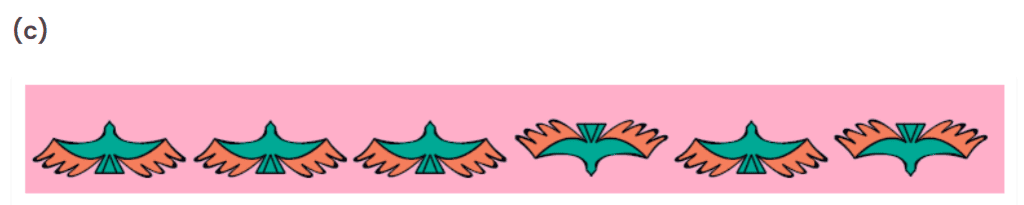
Observe the bird moving in upward direction and then downward.
So second bird should be in downward direction.
Ans: The picture marked below breaks the rule.
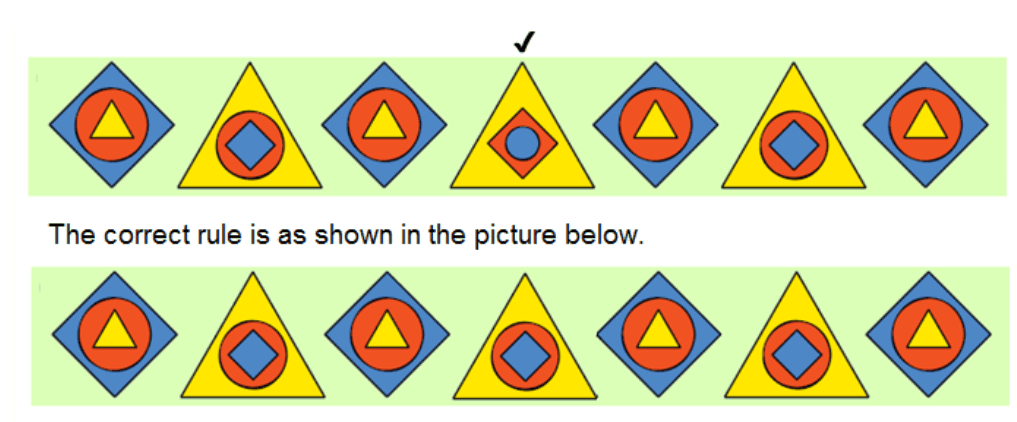
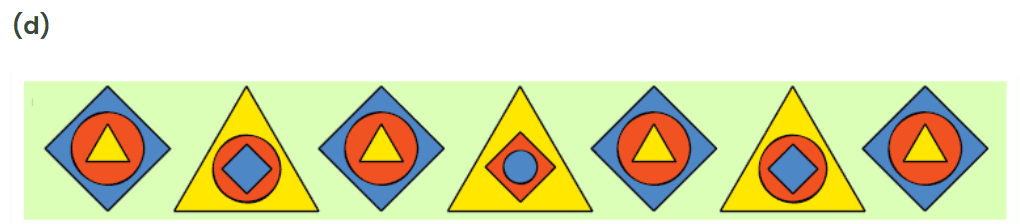
Observe this figure carefully.
First, circle is inside every shape and the fourth figure is breaking this rule.
5. Magic Squares
Do you remember magic triangles? Come now, let’s make some magic squares.
Q. Fill this square using all the numbers from 46 to 54.
Ans: In this magic square, the sum of each of the row of numbers (across down and diagonally) is always the same.
We have to complete the magic squares, remembering that the numbers in each line are equal to 150.
Clearly:
In 3rd row: The required number= 150-52-47=150-99=51
In 3rd column: The required number =150-49-47=150-96=54
In 2nd row: The required number = 150-46-54= 150-100=50
In 2nd column: The required number= 150-50-52= 150-102=188
In 1st row: The required number= 150-18-49=150-97= 53
Therefore, the complete magic square is

Q. Fill this square using all the numbers from 21 to 29.
Rule: The total of each side is 75.
Ans. Let us fix 26 on the top most left hand side box.
Taking the diagonal of the square, we have
26+25=51 and 75-51=24
Therefore, put 24 at the end of this diagonal.
Fix 22 on the top most-right side box.
Considering the diagonal containing 22, we find that:
22+25=47 and 75-47=28
Therefore, put 28 at the end of this diagonal.
Clearly,
In 1st row: The required number =75-(26+22) =75-48=27
In 1st column: The required number = 75-(26+28) =75-54=21
In 2nd row: The required number =75- (21+25) =75-46=29
In 2nd column: The required number =75-(28+24) =75-52=27
Therefore, the complete magic square is as shown below:

6. Magic Hexagons
Look at the patterns of numbers in hexagons. Each side has 2 circles and 1 box.

Look at the number 65 in the box. Which are the circles next to it? Can you see how the rule works?
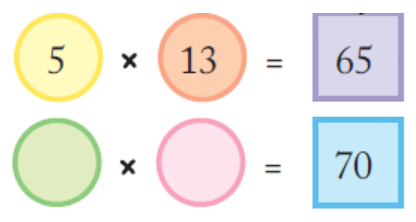
Ans: The circles next to 65 are 5 and 13.

The rule of this method is we get the number in each box by multiplying the numbers in the circles next to it.
(i) Use the same rule to fill the hexagons below.
(a) 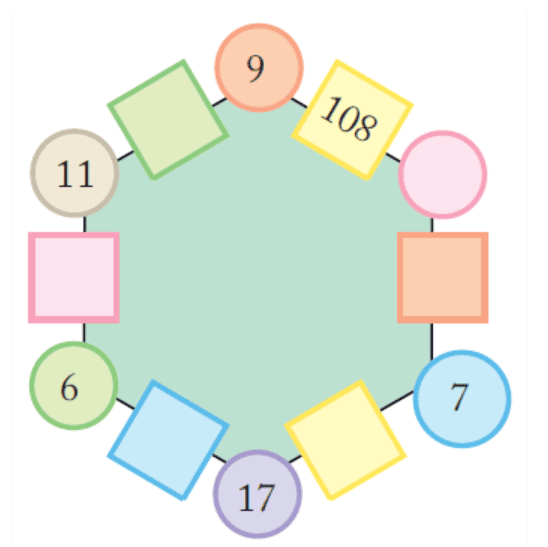
Ans: 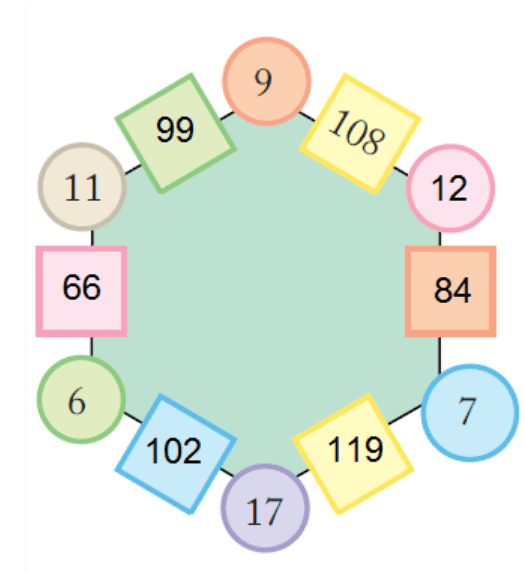
11 × 9 = 99
11 × 6 = 66
6 × 17 = 102
17 × 7 = 119
9 × 12 = 108
12 × 7 = 84
(b) 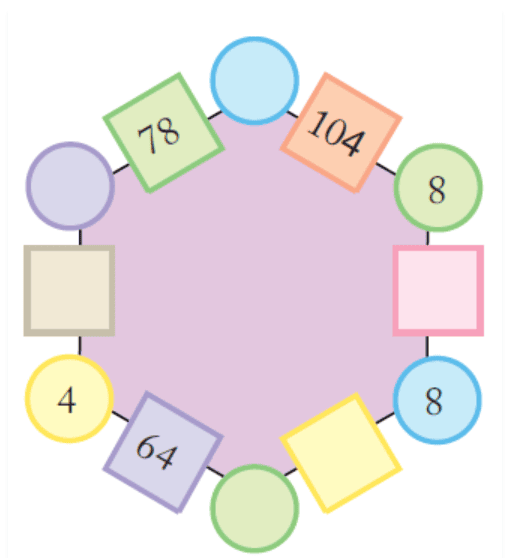
Ans: 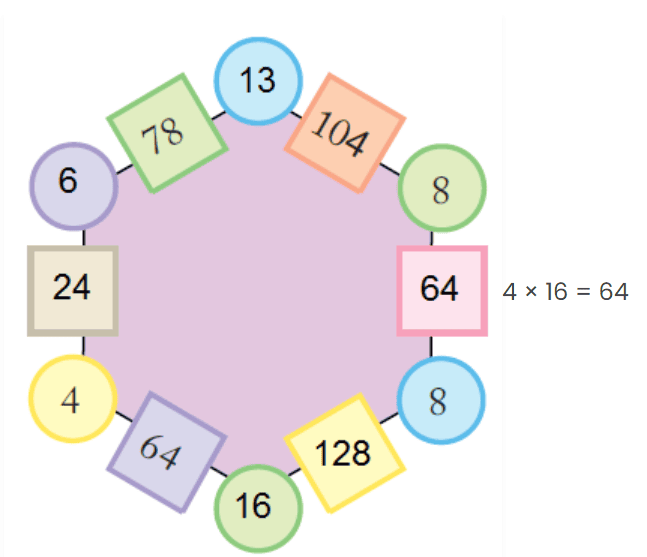
16 × 8 = 128
8 × 8 = 64
13 × 8 = 104
13 × 6 = 78
7. Numbers and Numbers
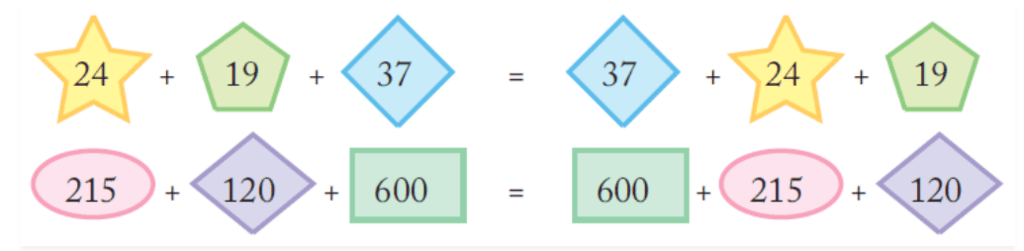
(i) Are they equal?
Ans: Yes, the mentioned equation are equal.
Let us consider the left-hand side (LHS) of the first equation = 24 + 19 + 37
LHS = 80
Now, the right-hand side (RHS) = 37 + 24 + 19
RHS = 80
By comparing LHS and RHS,
LHS = RHS
Then, consider second equation, LHS = 215 + 120 + 600
LHS = 935
Now, RHS = 600 + 215 + 120 = 935
By comparing LHS and RHS,
LHS = RHS
(ii) Fill in the blank spaces in the same way.
(a) 
Ans: 
See above explanation to answer these questions.
(b) 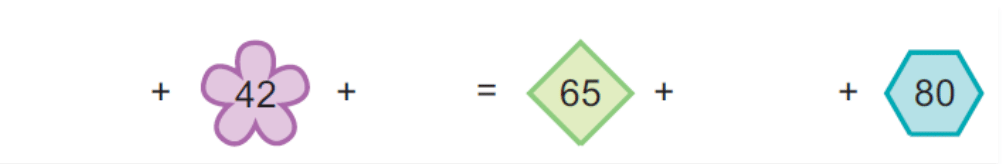
Ans: 
(c) 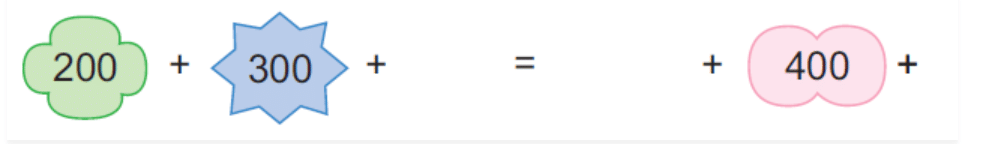
Ans: 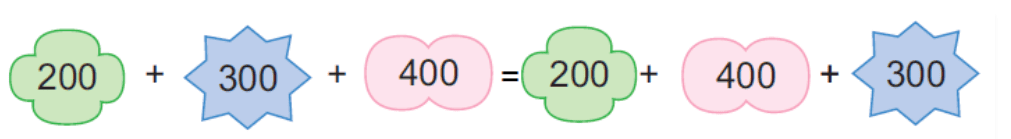
(d) 
Ans: 
(iii) Now, look at this –

Ans: First, consider the left-hand side (LHS) = 48 × 13
LHS = 624
Now, consider the right-hand side (RHS) = 13 × 48
RHS = 624
By comparing LHS and RHS,
LHS = RHS
(iv) Now you try and change these numbers into special numbers:
(a) 28 (b) 132 (c) 273
Ans: Imagine you're holding a magic mirror. When you look into it, some numbers stay the same no matter how you turn the mirror. These are called special numbers!
Let us see two fun ways these numbers become special:
(i) 
(ii) 
Now, let us try to change given numbers into special numbers:
(a)


(b)

(c)




(v) Now, let’s use words in a special way.

Did you notice that it reads the same from both sides — right to
left and left to right?
Now try and use words in a special way.
Ans: EYE, LEVEL, ROTATOR, NOON, REFER, etc.
8. Calendar Magic
Choose any 3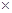 3 box from a calendar and find the total in the same way. Play this game with your family.
3 box from a calendar and find the total in the same way. Play this game with your family.
Ans:
Let us mark a 3 3 box (9 dates) on the calendar and see some magic.
3 box (9 dates) on the calendar and see some magic.

Take the smallest number: 2
Add 8 to it: +8
10
Multiply it by 9  9
9
Total 90
9. Some more Number Patterns
(i) Take any number. Now multiply it by 2, 3, …… at every step. Also add 3 to it at each step. Look at the difference in the answer. Is it the same at every step?
Ans: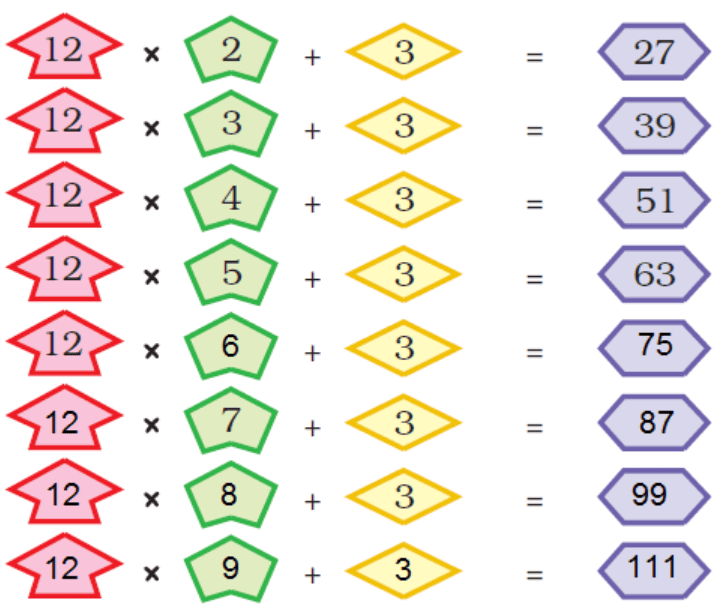
Let us check difference in the answer, 39 – 27 = 12, 51 – 39 = 12, 63 – 51 = 12,
75 – 63 = 12, 87 – 75 = 12, 99 – 87 = 12, 111 – 99 = 12
Therefore, the difference in the answer is the same at every step.
(ii) Look at the numbers below. Look for the pattern. Can you take it forward?

Ans:

In this sequence, each number precedes the next. It starts from 9 and by following the pattern it ends to 1.
(iii) Smart Adding
Ans: 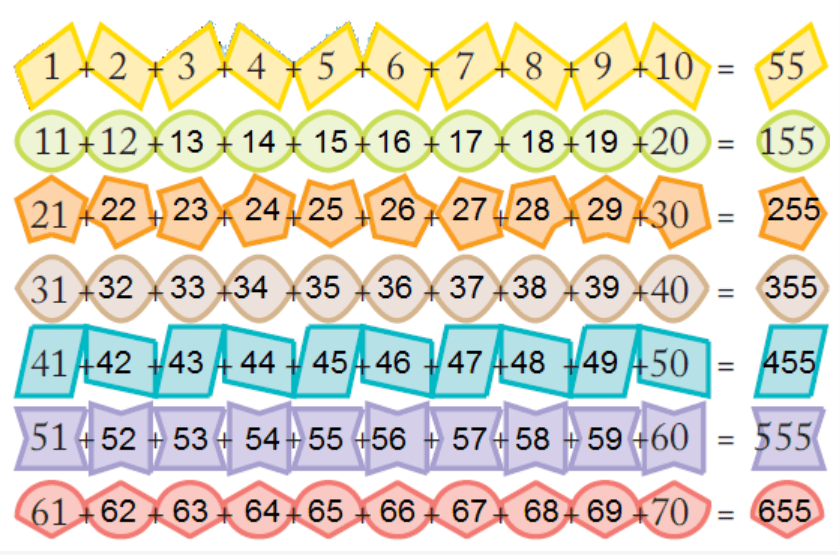
Did you notice some pattern in the answers?
Ans: Yes, I found that the difference in the answer is the same, i.e., 100 at every step.
10. Fun with Odd Numbers
Take the first two odd numbers, now add them, see what you get.Now, at every step, add the next odd number.
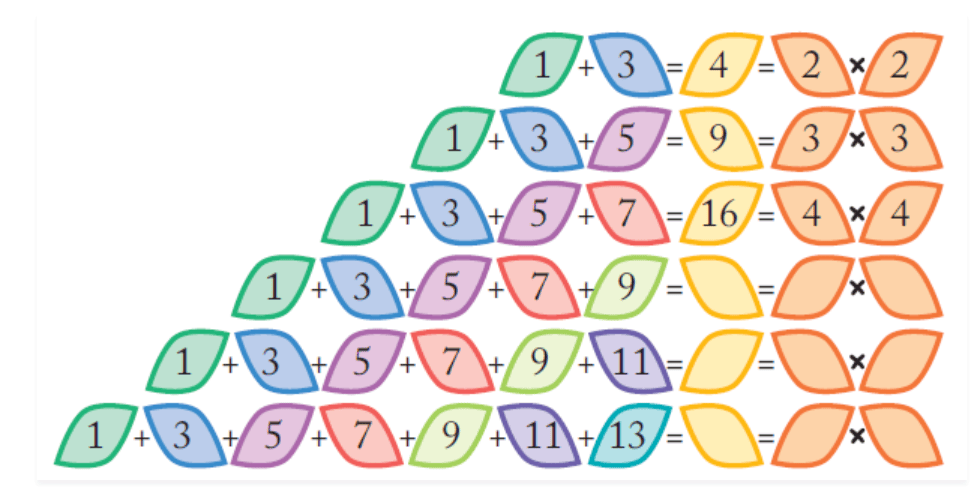
How far can you go on?
Ans: 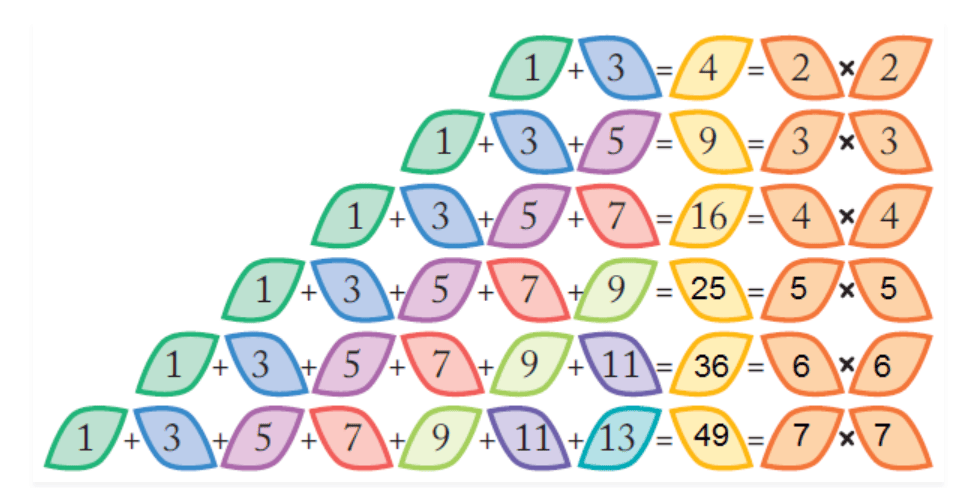
On R.H.S., numbers progress sequentially from 2 to 7.
On L.H.S, their squares are coming.
We can’t predict because there are infinite numbers.
11. Secret Numbers
(i) Banno and binod were playing a guessing game by writing clues about a secret number. Each tried by writing clues about a secret number. Each tried to guess the other’s secret number from the clues.
Can you guess their secret numbers?
1.
(a) It is larger than half of 100.
Ans: It is larger than half of 100 means > 50.
(b) It is more than 6 tens and less than 7 tens.
Ans: It is more than 6 tens and less than 7 tens it lies between 60 and 70.
(c) The tens digit is one more than he one’s digit.
Ans: The tens digit is one more than one’s digit is 6-5 =1.
(d) Together the digits have a sum of 11.
Ans: Together, the digits have a sum of 11, which means the number could be 65.
2.
(a) It is smaller than half of 100.
Ans: It is smaller than half of 100 means number < 50.
(b) It is more than 4 tens and less than 5 tens.
Ans: It is more than 4 tens and less than 5 tens, which means the number lies between 40 and 50.
(c) The tens digit is two more than the ones digit.
Ans: The tens digit is two more than the ones digit = 4 – 2 = 2
(d) Together the digits have a sum of 6.
Ans: Together, the digits have a sum of 6 = 4 + 2 = 6. Therefore, the number is 42.
(ii) Write a set of clues for a secret number of your own. Then give it to a friend to guess your secret answer.
Ans: A set of clues to find secret numbers are:
____ It is larger than half of 100.
It is more than 7 tens and less than 8 tens.
The tens digit is one less than the one’s digit.
Together the digits have a sum of 15.
The answer is 78.
12. Number Surprises
(i) Ask your friend-Write down his age. Add 5 to it. Multiply the sum by 2. Subtract 10 from it. Next divide it by 2. What do you get? Is your friend surprised?
Ans: Let us assume the age is 7
Add 5 to it: 7 + 5 =12
Multiply the sum by 2 = 12 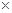 2 =24
2 =24
Subtract 10 from it: 24 -10 =14
Divide it by 2 =14/2= 7
Yes, My friend was very surprised.
b) 
Ans:
c) 
Ans: 
d) 
Ans:
1 = 1 × 1
121 = 11 × 11
12321 = 111 × 111
1234321 = 1111 × 1111
123454321 = 11111 × 11111
12345654321 = 111111 × 111111
1234567654321 = 1111111 × 1111111
1234567654321 = 1111111 × 1111111
1234567654321 = 1111111 × 1111111
|
28 videos|169 docs|41 tests
|
FAQs on NCERT Solutions for Class 5 Maths - Can you See The Pattern
| 1. What are the key concepts covered in the "Can You See the Pattern?" chapter? |  |
| 2. How can patterns be identified in daily life? |  |
| 3. Why is recognizing patterns important in mathematics? |  |
| 4. What types of exercises are included in the chapter to practice pattern recognition? |  |
| 5. How can students improve their pattern recognition skills? |  |

|
Explore Courses for Class 5 exam
|

|


















