NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 3 (Exercise 3.3)
Exercise 3.3
Q1: Given a parallelogram ABCD. Complete each statement along with the definition or property used.
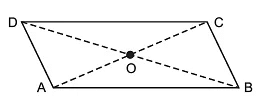 (i) AD = _____
(i) AD = _____
(ii) ∠DCB = _____
(iii) OC = _____
(iv) m∠DAB + m∠CDA = _____
Sol:
(i) AD = BC [∵ Opposite sides are equal]
(ii) ∠DCB = ∠DAB [∵ Opposite angles are equal]
(iii) OC = OA [∵ Diagonals bisect each other]
(iv) m∠DAB + m∠CDA = 180° [∵ Adjacent angles are supplementary]
Q2: Consider the following parallelograms. Find the values of the unknowns x, y, z.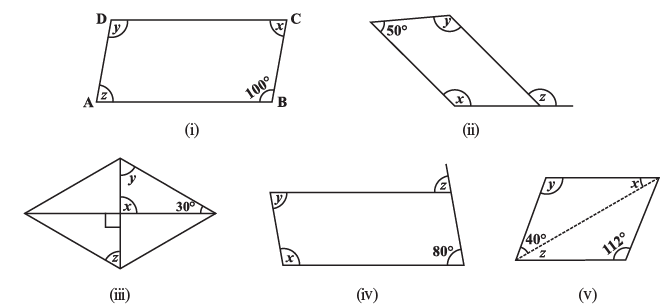
Sol: (i) ∠y = 100° [∵ Opposite angles of a parallelogram are equal.]
∵ Sum of interior angles of a parallelogram = 360°
∴ x + y + z + ∠B = 360°
or x + 100° + z + 100° = 360°
or x + z = 360° – 100° – 100° = 160°
But x = z [∵ Opposite angles of a parallelogram are equal.]
∴ x = z = 160°/2 = 80°
Thus,
(ii)∵ Opposite angles of a parallelogram are equal
∴ ∠1 = 50°
Now, ∠1 + z = 180° [Linear pair]
or z = 180° – ∠1 = 180° – 50° = 130°
x + y + 50° + 50° = 360°
or x + y = 360° – 50° – 50° = 260°
But x = y
∴ x = y = 260°/2° = 130°
(iii) ∵ Vertically opposite angles are equal,∴ x = 90°
∵ Sum of the angles of a triangle = 180°∴90° + 30° + y = 180°
or y = 180° – 30° – 90° = 60°
In the figure, ABCD is a parallelogram.
∴ AD || BC and BD is a transversal.
∴ y = z [as y and z are Alternate angles]
But y = 60°
∴ z = 60°
Thus, x = 90°, y = 60° and z = 60°.
(iv) ABCD is a parallelogram.∴ Opposite angles are equal.
∴ y = 80°
AB || CD and BC is a transversal.
∴ x + 80° = 180° [as x and C are Interior opposite angles]
or x = 180° – 80° = 100°
Again BC || AD and CD is a transversal,
∴ z = 80° [as C and z are Corresponding angles]
Thus, x = 100°, y = 80° and z = 80°
(v) ∵ In a parallelogram, opposite angles are equal.∴ y = 112°
In Δ ACD,
x + y + 40° = 180°
x + 112° + 40° = 180°
∴ x = 180° – 112° – 40° = 28°
∵ AD || BC and AC is a transversal.
∴ x = z [∵ Alternate angles are equal]
and z = 28°
Thus, x = 28°, y = 112° and z = 28°
Q3: Can a quadrilateral ABCD be a parallelogram if
(i) ∠A + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) ∠A = 70° and ∠C = 65°?
Sol: (i) In a quadrilateral ABCD,
∠A + ∠B = Sum of adjacent angles = 180°
∴ The quadrilateral may be a parallelogram but not always.
(ii) In a quadrilateral ABDC,
AB = DC = 8 cm
AD = 4 cm
BC = 4.4 cm
∵ Opposite sides AD and BC are not equal.
∴ It cannot be a parallelogram.
(iii) In a quadrilateral ABCD,
∠A = 70° and ∠C = 65°
∵ Opposite angles ∠A ≠ ∠C
∴ It cannot be a parallelogram.
Q4: Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Sol:
ABCD is a figure of quadrilateral that is not a parallelogram but has exactly two opposite angles, that is, ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.
Q5: The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the
parallelogram.
Sol: Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x, respectively in parallelogram ABCD.
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
We know that opposite sides of a parallelogram are equal.
∠A = ∠C = 3x = 3 × 36° = 108°
∠B = ∠D = 2x = 2 × 36° = 72°
Q6: Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Sol: Let ABCD be a parallelogram.
Sum of adjacent angles of a parallelogram = 180°
∠A + ∠B = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
also, 90° + ∠B = 180°
⇒ ∠B = 180° – 90° = 90°
∠A = ∠C = 90°
∠B = ∠D = 90°
Q7: The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.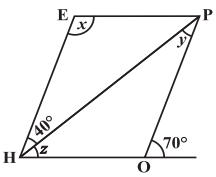
Sol: y + z = 70° …(1)
In a triangle, exterior angles is equal to the sum of interior angles opposite to the exterior angle.∴ In Δ ∠HOP, ∠HOP = 180° -(y + z)
= 180° – 70°
= 110°
Now x = ∠HOP [Opposite angles of a parallelogram are equal]
∴ x = 110° EH || OP and PH is a transversal.
∴ y = 40° [Alternate angles are equal]
From (1), 40° + z = 70°
∴ z = 70° – 40° = 30°
Thus, x = 110°, y = 40° and z = 30°
Q8: The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)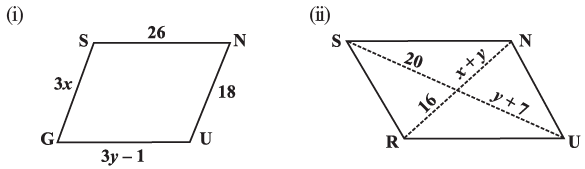
Sol: (i) ∵ GUNS is a parallelogram.
∴ Its opposite sides are equal.
∴ GS = NU and SN = GU
or 3x = 18 and 26 = 3y – 1
Now 3x = 18
⇒ x = 18/3 = 6
3y – 1 = 26
⇒ y = (26 + 1)/3 = 27/3 = 9
Thus, x = 6 cm and y = 9 cm
(ii) RUNS is a parallelogram and thus its diagonals bisect each other.
∴ x + y = 16 and 7 + y = 20
i.e. y = 20 – 7
or y = 13
∴ From x + y = 16, we have
x + 13 = 16
or x = 16 – 13 = 3Thus, x = 3 cm and y = 13 cm.
Q9: In the following figure, both RISK and CLUE are parallelogram. Find the value of x.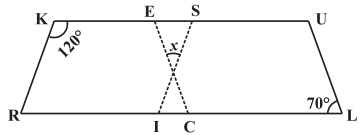
Sol: ∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL (corresponding angles)
⇒ ∠SIL = 60°
Also, ∠ECR = ∠L = 70° (corresponding angles) x + 60° + 70° = 180° (angle sum of a triangle)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Q10: Explain how this figure is a trapezium. Which of its two sides are parallel?
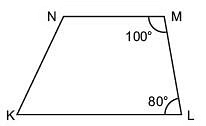
Sol: Since, 100° + 80° = 180°
i.e. ∠M and ∠L are supplementary.[∵ If interior opposite angles along the transversal are supplementary]
Q11: Find m∠C in the adjoining figure if .
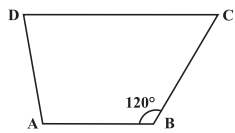
Sol: ∵ ABCD is a trapezium in which
and BC is a transversal.
∴ Interior opposite angles along BC are supplementary.
∴ m∠B + m∠C = 180°
or m∠C = 180° – m∠B
∴ m∠C = 180° – 120° [∵ ∠B = 120°]
or m∠C = 60°
Q12: Find the measure of ∠P and ∠ S if in figure. (If you find m∠R, is there more than one method to find m∠P?)
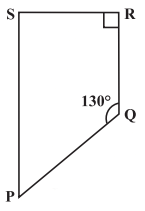
Sol: ∠P + ∠Q = 180° (angles on the same side of transversal)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles is 360°.
Since, we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Exercise 3.4
Q1: State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All square are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Sol: (a) False
Reason: Rectangles have opposite sides of equal length and all angles are 90 degrees, while squares have all sides of equal length and all angles are 90 degrees. Therefore, not all rectangles are squares.(b) True
Reason: A rhombus is a type of parallelogram with all sides of equal length. Therefore, all rhombuses are also parallelograms.(c) True
Reason: A square is a special case of both a rhombus and a rectangle. It has all sides of equal length (making it a rhombus) and all angles are 90 degrees (making it a rectangle).(d) False
Reason: All squares are actually parallelograms. A square is a type of parallelogram with all sides of equal length and all angles equal to 90 degrees.(e) False
Reason: While all kites have two pairs of adjacent sides that are equal, not all kites have all sides equal. A rhombus has all sides equal, so it is a specific type of kite, but not all kites are rhombuses.(f) True
Reason: A rhombus is a type of kite due to its two pairs of adjacent sides being equal. Therefore, not all rhombuses are kites.(g) True
Reason: A trapezium (also known as a trapezoid in some regions) is a quadrilateral with at least one pair of parallel sides. Since a parallelogram has both pairs of opposite sides parallel, it can also be considered a trapezium.(h) True
Reason: A square is a type of parallelogram because it has both pairs of opposite sides parallel. Therefore, all squares are also trapeziums.
Q2: Identify all the quadrilaterals that have:
(a) Four sides of equal length.
(b) Four right angles.
Sol: (a) Squares as well as rhombus have four sides of equal length.
(b) Squares as well as rectangles have four right-angles.
Q3: Explain how a square is:
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Sol:
(i) A square is a 4 sided figure, so it is a quadrilateral.
(ii) The opposite sides of a square are equal and parallel, so it is a parallelogram.
(iii) All the sides of a square are equal, so it is a rhombus.
(iv) Each angle of a square is a right angle, so it is a rectangle.
Q4: Name the quadrilaterals whose diagonal:
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Sol: (i) The diagonals of the following quadrilaterals bisect each other:
Parallelogram, rectangle, square, rhombus
(ii) The diagonals are perpendicular bisectors of the following quadrilaterals:
Square and rhombus
(iii) The diagonals are equal in case of:
Square and rectangle
Q5: Explain why a rectangle is a convex quadrilateral.
Sol: (i) All the angles have measures less than 180°.
(ii) Both diagonals lie wholly in the interior of the rectangle.
∴ The rectangle is a convex quadrilateral.
Q6: ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
Sol: Produce BO to D such that BO = OD.
Joining CD and AD, we get a quadrilateral ABCD in which opposite sides are parallel.
∴ ABCD is a parallelogram.
∵ ∠ABC = 90°
∴ ABCD is a rectangle.
Since, diagonals of a rectangle bisect each other, i.e. O is the mid-point of BD and AC .
∴ O is equidistant from A, B and C.
|
81 videos|423 docs|31 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 3 (Exercise 3.3)
| 1. What are the properties of a quadrilateral? |  |
| 2. How can we classify quadrilaterals based on their properties? |  |
| 3. Can a quadrilateral have all its angles as right angles? |  |
| 4. How do we calculate the area of a quadrilateral? |  |
| 5. What is the difference between a rhombus and a square? |  |


















