NCERT Solutions for Class 8 Maths Chapter 4 - Ex 4.1 and 4.2 Practical Geometry - 1
EXERCISE 4.1
Question 1. Construct the following quadrilaterals.
(i) Quadrilateral ABCD
AB = 45 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm
(ii) Quadrilateral JUMP
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm
(iii) Parallelogram MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm
(iv) Rhombus BEST
BE = 4.5 cm
ET = 6 cm
Solution:
Note: Before making a fair construction for each of the above quadrilaterals, a rough sketch must be drawn and the given measurements be marked.
(i) Steps of construction:
I. Draw a line segments AB = 4.5 cm.
II. With centre at A and radius = 7 cm, draw an arc.
III. With centre at B and radius = 5.5 cm, draw another arc to intersect the previous arc at C.
IV. With centre at A and radius = 6 cm, draw an arc on the side opposite to that of B.
V. With centre at C and radius = 4 cm, draw another arc to intersect the previous arc at D.
VI. Join AC, BC, DA and DC.
Thus, ABCD is the required quadrilateral.
(ii) Steps of construction:
I. Draw a line segment JU = 3.5 cm.
II. With centre at U and radius UP = 6.5 cm, draw an arc.
III. With centre at J and radius = 4.5 cm, draw another arc to intersect the previous arc at P.
IV. With centre at U and radius = 4 cm, draw an arc on the side opposite to that of J.
V. With centre at P and radius = 4 cm, draw another arc intersecting the previous arc at M.
VI. Join PJ, PU, PM and UM.
Thus, JUMP is the required quadrilateral.
(iii) Steps of construction:
I. Draw a line segments ER = 4.5 cm.
II. With centre at E and radius = 7.5 cm, draw an arc.
III. With centre at R and radius = 6 cm, draw another arc to intersect the previous are at O.
IV. With centre at R and radius = 6 cm, draw an are on the side opposite to R.
V. With centre at O and radius = 4.5 cm, draw another arc to intersect the previous arc at M.
VI. Join RO, EM, EO and MO.
Thus, EROM or MORE is the required parallelogram.
(iv) Steps of construction:
I. Draw a line segment BE = 4.5 cm.
II. With centre at E and radius = 6 cm, draw an arc.
III. With centre at B and radius = 4.5 cm, draw another arc to intersect the previous arc at T.
Note: All the 4 sides of a rhombus are equal.
IV. Join TB and TE.
V. With centre at T and radius = 4.5 cm, draw an arc on the side opposite to that of B.
VI. With centre at E and radius = 4.5 cm, draw another arc to intersect the previous arc at S.
VII. Join ST and SE Thus, BEST is the required quadrilateral.
Some other Solved Examples
Question 1: Arshad has five measurements of a quadrilateral ABCD. These are AB = 5 cm, ∠A = 50°, AC = 4 cm, BD = 5 cm and AD = 6 cm. Can he construct a unique quadrilateral? Give reasons for your answer.
Solution:
No, Arshad cannot construct a unique quadrilateral with the given measurements.
Reasons:
1. There is no information about the angles between the given sides. For example, we don't know the value of ∠B, ∠C, or ∠D, which are necessary to uniquely construct the quadrilateral.
2. There is no information about the length of the diagonal BD or the relationship between the given sides and angles, such as whether the quadrilateral is a parallelogram or a rectangle.
3. The given information is not sufficient to apply any known quadrilateral properties or theorems, such as the Law of Cosines or the Law of Sines, to calculate the missing side lengths or angles.
Question 2: (i) We saw that 5 measurements of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurements of the quadrilateral can do this?
(ii) Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and AS = 6.5cm?
Why?
(iii) Can you draw a rhombus ZEAL where ZE = 3.5 cm, diagonal EL = 5 cm? Why?
(iv) A student attempted to draw a quadrilateral PLAY where PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm, but could not draw it. What is the reason?
Hint: Discuss it using a rough sketch.
Solution:
(i) No, any 5 measurements (elements) cannot determine a quadrilateral. Actually to construct a quadrilateral, we need a specific combination of measurements such as:
(a) Four sides and one diagonal
or
(b) Three sides and two diagonals
or
(c) Two adjacent sides and three angles
or
(d) Three sides and two included angles.
or
(e) Some special properties are given.
(ii) Let us draw a rough sketch of BATS as given.
Here, we cannot locate the points T and B without knowing the measurements ST and SB respectively.
Thus, we cannot draw a parallelogram with the given measurements.
(iii) Let us draw a rough sketch of the (rhombus) quadrilateral ZEAL and mark the given measurements on it.
Since all sides of Rhombus are given and they are equal to 3.5 cm and a diagonal EL is also known.
Therefore, we can draw the required rhombus ZEAL.
(iv) Let us draw the rough sketch of the quadrilateral PLAY and mark its measurements,
∵ Point P cannot be located. In D LPY, sum of the lengths of PL and PY is less than LY, i.e. (2 cm + 3 cm) < 6 cm.
Therefore, this quadrilateral cannot be drawn.
CONSTRUCTION OF A QUADRILATERAL WHEN ITS TWO DIAGONALS AND THREE SIDES ARE KNOWN
In this case, we take one of the diagonal as the base of a triangle, then taking any two the given sides, we locate the vertex (third point of the quadrilateral) of the triangle. Again, using the second diagonal and third given side, we locate the fourth point of the quadrilateral.
EXERCISE 4.2
Question 1. Construct the following quadrilaterals.
(i) Quadrilateral LIFT
LI = 4 cm
I F = 3 cm
TL = 2.5 cm
LF = 4.5 cm
IT = 4 cm
(ii) Quadrilateral GOLD
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm
(iii) Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
Solution: (i) Steps of constructions:
I. Draw a line segment LI = 4 cm.
II. With centre at I and radius = 4 cm, draw an arc.
III. With centre at L and radius = 2.5 cm, draw another arc to intersect the previous arc at T.
IV. Join TI and TL.
V. With centre I and radius = 3 cm, draw an arc on the side opposite to that of L.
VI. With centre at L and radius = 4.5 cm, draw another arc to intersect the previous arc at F.
VII. Join FL and FI.
Thus, LIFT is the required quadrilateral.
(ii) Steps of construction:
I. Draw a line segment LD = 5 cm.
II. With centre at L and radius = 6 cm, draw an arc.
III. With centre at D and radius = 6 cm, draw another arc to intersect the previous arc at G.
IV. Join GL and GD.
V. With centre at D and radius = 10 cm, draw an arc on the same side as that of G.
VI. With centre at L and radius = 7.5 cm, draw another arc to intersect the previous arc at O.
VII. Join OL and OD.
Thus, GOLD is the required quadrilateral.
(iii) Steps of construction:
I. Draw a line segment DE = 6.5 cm.
II. Draw perpendicular bisector PQ of DE such that M being the mid-point of DE.
III. With centre M and radius 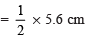 = 2.8 cm, draw arcs to intersect PQ at B and N.
= 2.8 cm, draw arcs to intersect PQ at B and N.
IV. Join ND, NE, BE and BD.
Thus, BEND is the required rhombus.
Some other Solved Examples
Question 1. “Construct a quadrilateral ABCD, given that BC = 4.5 cm, AD = 5.5 cm, CD = 5 cm, the diagonal AC = 5.5 cm and diagonal BD = 7 cm.” Can we draw the quadrilateral by drawing triangle ABD first and then find the fourth point C?
Solution: Since, the measurement of AB is not given.
Therefore we cannot draw triangle ABD and hence it is not possible to draw quadrilateral ABCD by drawing triangle ABD.
|
Question 2. Can you construct a quadrilateral PQRS with PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and SQ = 4 cm? Justify your answer
Solution: Yes a quadrilateral PQRS can be drawn using PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and SQ = 4 cm.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 4 - Ex 4.1 and 4.2 Practical Geometry - 1
| 1. What are the basic principles of practical geometry? |  |
| 2. How can I construct an equilateral triangle using practical geometry? |  |
| 3. Can practical geometry be used in real-life applications? |  |
| 4. What is the difference between practical geometry and theoretical geometry? |  |
| 5. What are the common tools used in practical geometry? |  |

















