NCERT Solutions for Class 8 Maths - Fractions and Decimals (Exercise 2.2 and 2.3)
Exercise 2.2
 Fractions and Decimals
Fractions and Decimals
Q1. Find:
(i) 1/4 of
(a) 1/4
(b) 3/5
(c) 4/3
(ii) 1/7 of
(a) 2/9
(b) 6/5
(c) 3/10
Ans:
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
(i)
(a)
(b)
(c)(ii)
(a)
(b)
(c)
Q2: Multiply and reduce to lowest form (if possible):
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Ans:
(i) First, convert the given mixed fraction into an improper fraction.
== 8/3,
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,(ii) By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,(iii) By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,(iv) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(v) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vi) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vii) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
 Multiplying FractionQ3. Multiply the following fractions:
Multiplying FractionQ3. Multiply the following fractions:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Ans:
(i) First convert the given mixed fraction into improper fraction.
= 5 ¼ = 21/4
Now,
= (2/5) × (21/4)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(ii) First, convert the given mixed fraction into an improper fraction.
== 32/5Now,= (32/5) × (7/9)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,(iii) First, convert the given mixed fraction into an improper fraction.
== 16/3
Now,
= (3/2) × (16/3)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(iv) First convert the given mixed fraction into an improper fraction.
== 17/7
Now,
= (5/6) × (17/7)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(v) First convert the given mixed fraction into improper fraction.
== 17/5
Now,
= (17/5) × (4/7)By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vi) First convert the given mixed fraction into improper fraction.
== 13/5
Now,
= (13/5) × (3/1)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vii) First convert the given mixed fraction into improper fraction.
== 25/7
Now,
= (25/7) × (3/5)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
Q4. Which is greater:
(i)
(ii)
Ans:
(i)
⇒
⇒
⇒
(ii)
⇒
⇒
⇒
Q5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is 3/4 m. Find the distance between the first and the last sapling.
Ans: The distance between two adjacent saplings = 3/4 m
Saili planted 4 saplings in a row, then number of gap in saplings = 3
Therefore,
The distance between the first and the last saplings
Thus the distance between the first and the last saplings is
Q6. Lipika reads a book forhours every day. She reads the entire book in 6 days. How many hours in ail were required by her to read the book?
Ans: Time is taken by Lipika to read a book =
hours
She reads the entire book in 6 days.
Now, the total hours are taken by her to read the entire book
Thus, 10 hours were required by her to read the book.
Q7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using of petrol?
Ans: In 1 litre of petrol, car covers the distance = 16 km
Inlitres of petrol, car covers the distance =
Thus, the car will cover 44 km distance.
Q8.
(a)
(i) Provide the number in the box
(ii) The simplest form of the number obtained in
(b)
(i) Provide the number in the box
(ii) The simplest form of the number obtained in
Ans:
(a)
(ii) The simplest form
(b)
(ii) The simplest form
Exercise 2.3
Q1.
Find:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Ans:
(i) We have,
= 12 × reciprocal of ¾
(ii) We have,
= 14 × reciprocal of (5/6)
(iii) We have,
= 8× reciprocal of (7/3)
(iv) We have,
= 4 × reciprocal of (8/3)
(v) While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction We have,
== 7/3
Then,
= 3 ÷ (7/3)
= 3 × reciprocal of (7/3)
(vi) While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction We have,
== 25/7
Then,
= 5 ÷ (25/7)
= 5 × reciprocal of (25/7)
Q2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i) 3/7
Ans: Reciprocal of (3/7) is (7/3) [∵ ((3/7) × (7/3)) = 1]
So, it is an improper fraction.
Improper fraction is that fraction in which numerator is greater than its denominator.
(ii) 5/8
Ans: Reciprocal of (5/8) is (8/5) [∵ ((5/8) × (8/5)) = 1]
So, it is an improper fraction.
Improper fraction is that fraction in which numerator is greater than its denominator.
(iii) 9/7
Ans: Reciprocal of (9/7) is (7/9) [∵ ((9/7) × (7/9)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(iv) 6/5
Ans: Reciprocal of (6/5) is (5/6) [∵ ((6/5) × (5/6)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(v) 12/7
Ans: Reciprocal of (12/7) is (7/12) [∵ ((12/7) × (7/12)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(vi) 1/8
Ans: Reciprocal of (1/8) is (8/1) or 8 [∵ ((1/8) × (8/1)) = 1]
So, it is a whole number.
Whole numbers are collection of all positive integers including 0.
(vii) 1/11
Ans: Reciprocal of (1/11) is (11/1) or 11 [∵ ((1/11) × (11/1)) = 1]
So, it is a whole number.
Whole numbers are collection of all positive integers including 0.
Q3. Find:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Ans:
(i) We have,
= (7/3) × reciprocal of 2
= (7/3) × (1/2)
(ii) We have,
= (4/9) × reciprocal of 5
= (4/9) × (1/5)
(iii) We have,
= (6/13) × reciprocal of 7
= (6/13) × (1/7)
(iv) First convert the mixed fraction into improper fraction. We have,
== 13/3 Then,
= (13/3) × reciprocal of 3
(v) First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of 4
(vi) First convert the mixed fraction into improper fraction.
We have,=
= 31/7
Then,
= (31/7) × reciprocal of 7
Q4. Find
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
Ans:
(i) We have,
= (2/5) × reciprocal of ½
= (2/5) × (2/1)
(ii) We have,
= (4/9) × reciprocal of (2/3)
= (4/9) × (3/2)
(iii) We have,
= (3/7) × reciprocal of (8/7)
= (3/7) × (7/8)
(iv) First convert the mixed fraction into improper fraction.
We have,
== 7/3
Then,
= (7/3) × reciprocal of (3/5)
(v) First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of (8/3)
= (7/2) × (3/8)
(vi) First convert the mixed fraction into improper fraction.
We have,
= 1 ½ = 3/2
Then,
= (2/5) × reciprocal of (3/2)= (2/5) × (2/3)
(vii) First convert the mixed fraction into improper fraction.
We have,
== 16/5
=
= 5/3Then,= (16/5) × reciprocal of (5/3)= (16/5) × (3/5)
(viii) First convert the mixed fraction into improper fraction.
We have,
== 11/5
=
= 6/5
Then,
= (11/5) × reciprocal of (6/5)
= (11/5) × (5/6)
Deleted Exercise
Q1: Which is greater:
(i) 0.5 or 0.05
(ii) 0.7or 0.5
(iii) 7 or 0.7
(iv) 1.37 or 1.49
(v) 3.03 or 2.30
(vi) 0.8 or 0.88
Ans:
(i) 0.5 > 0.05
(ii) 0.7 > 0.5
(iii) 7 >0.7
(iv) 1.37 <1.49
(v) 2.03 < 2.30
(vi) 0.8 <0.88
Q2: Express as rupees using decimals:
(i) 7 paise
(ii) 7 rupees 7 paise
(iii) 77 rupees 77 paise
(iv) 50 paise
(v) 235 paise
Ans: We know that,
∵
∴
(i)
(ii)
(iii)
(iv)
(v)
Q3:
(i) Express 5 cm in metre and kilometre.
(ii) Express 35 mm in cm, m and km.
Ans:
(i) Express 5 cm in meter and kilometer.
We know that, 100 cm = 1 meter
∴ 1 cm = 1/100 meter
⇒ 5 cm = 5/100 = 0.05 meter
Now,
∴ 1000 meters = 1 kilometers
∴ 1 meters = 1/1000 kilometer
⇒ 0.05 meter = 0.05/1000 = 0.00005 kilometer
(ii) Express 35 mm in cm, m and km.
∵ 10 mm = 1 cm
∴ 1 mm = 1/10 cm
⇒ 35 mm = 35/100 = 3.5 cm
Now, ∵ 100 cm = 1 meter
∴ 1 cm = 1/100 meter
⇒ 3.5 cm = 3.5/100 = 0.035 meter
Again,
∵ 1000 meters = 1 kilometers
∴ 1 meter = 1/1000 kilometers
⇒ 0.035 meter = 0.035/1000 = 0.000035 kilometer
Q4: Express in kg.
(i) 200 g
(ii) 3470 g
(iii) 4 kg 8 g
Ans:
Let us consider, 1000 g = 1 kg
⇒
(i)
(ii)
(iii) 4kg 8 g = 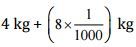 = 5 kg + 0.008 kg = 4.005 kg
= 5 kg + 0.008 kg = 4.005 kg
Q5: Write the following decimal numbers in the expanded form:
(i) 20.03
(ii) 2.03
(iii) 200.03
(iv) 2.034
Ans:
(i)
(ii)
(iii)
(iv)
Q6: Write the place value of 2 in the following decimal numbers:
(i) 2.56
(ii) 21.37
(iii) 10.25
(iv) 9.42
(v) 63.352
Ans:
(i) Place value of 2 in 2.56 = 2 x 1 = 2 ones
(ii) Place value of 2 in 21.37 = 2 x 10 = 2 tens
(iii) Place value of 2 in 10.25 
(iv) Place value of 2 in 9.42 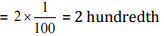
(v) Place value of 2 in 63.352 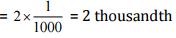
Q7: Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?
Ans:
Distance travelled by Dinesh when he went from place A to place B = 7.5 km and from place B to C = 12.7 km.
Total distance covered by Dinesh = AB + BC
= 7.5 + 12.7
= 20.2 km
Total distance covered by Ayub = AD + DC
= 9.3 + 11.8
= 21.1 km
On comparing the total distance of Ayub and Dinesh,
21.1 km > 20.2 km
Therefore, Ayub covered more distance by 21.1 – 20.2 = 0.9 km = 900 m
∴Ayub travelled 0.9 km more than Dinesh.
Q8: Shyam bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
Ans: From the question, it is given that, Fruits bought by Shyama = 5 kg 300 g
= 5 kg + (300/1000) kg
= 5 kg + 0.3 kg
= 5.3 kg
Fruits bought by Sarala = 4 kg 800 g + 4 kg 150 g
= (4 + (800/1000)) + (4 + (150/1000))
= (4 + 0.8) kg + (4 + .150) kg
= 4.8 kg + 4.150kg
= 8.950 kg
So, Sarala bought more fruits.
Q9: How much less is 28 km than 42.6 km?
Ans:
We have to find the difference between 42.6 km and 28 km.
Difference = 42.6 – 28.0 = 14.6 km
Therefore,14.6 km less is 28 km than 42.6 km.
FAQs on NCERT Solutions for Class 8 Maths - Fractions and Decimals (Exercise 2.2 and 2.3)
| 1. What are fractions and decimals? |  |
| 2. What is the difference between a fraction and a decimal? |  |
| 3. How are fractions and decimals related? |  |
| 4. How can fractions and decimals be used in everyday life? |  |
| 5. What are some common operations performed with fractions and decimals? |  |

 = 8/3,
= 8/3,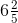 = 32/5Now,= (32/5) × (7/9)
= 32/5Now,= (32/5) × (7/9)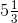 = 16/3
= 16/3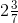 = 17/7
= 17/7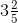 = 17/5
= 17/5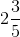 = 13/5
= 13/5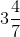 = 25/7
= 25/7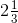 = 7/3
= 7/3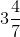 = 25/7
= 25/7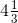 = 13/3 Then,
= 13/3 Then,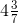 = 31/7
= 31/7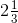 = 7/3
= 7/3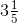 = 16/5
= 16/5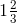 = 5/3Then,= (16/5) × reciprocal of (5/3)= (16/5) × (3/5)
= 5/3Then,= (16/5) × reciprocal of (5/3)= (16/5) × (3/5)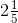 = 11/5
= 11/5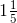 = 6/5
= 6/5


























