NCERT Solutions for Class 9 - Maths Circles Exercise 9.1
Exercise 9.1
Q1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Ans: To recall, a circle is a collection of points whose every point is equidistant from its centre. So, two circles can be congruent only when the distance of every point of both circles is equal from the centre.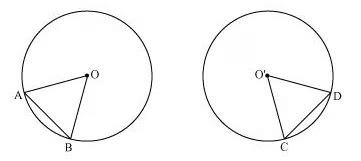 In the second part of the question, it is given that AB = CD, i.e. two equal chords. Now, it is to be proven that angle AOB is equal to angle COD.
In the second part of the question, it is given that AB = CD, i.e. two equal chords. Now, it is to be proven that angle AOB is equal to angle COD.
Proof:
Consider the triangles ΔAOB and ΔCOD,
OA = OC and OB = OD (Since they are the radii of the circle)
AB = CD (As given in the question)
So, by SSS congruency, ΔAOB ≅ ΔCOD
∴ By CPCT, we get
∠AOB = ∠COD.
Hence proved.
Q2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Ans: Consider the following diagram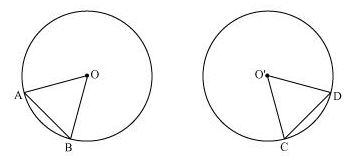 Here, it is given that ∠AOB = ∠COD, i.e. they are equal angles. Now, we will have to prove that the line segments AB and CD are equal, i.e. AB = CD.
Here, it is given that ∠AOB = ∠COD, i.e. they are equal angles. Now, we will have to prove that the line segments AB and CD are equal, i.e. AB = CD.
Proof:
In triangles ΔAOB and ΔCOD,
∠AOB = ∠COD (as given in the question)
OA = OC and OB = OD (these are the radii of the circle)
So, by SAS congruency, ΔAOB ≅ ΔCOD.
∴ By the rule of CPCT, we get AB = CD.
Hence proved.
Exercise 9.2
Ans: Given parameters are:
OP = 5cm
OS = 4cm and
PS = 3cm
Also, PQ = 2PR
Now, suppose RS = x. The diagram for the same is shown below.
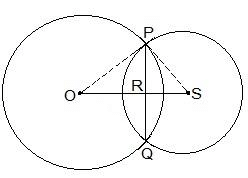 Consider the ΔPOR,
Consider the ΔPOR,OP2 = OR2 + PR2
⇒ 52 = (4 - x)2 + PR2
⇒ 25 = 16 + x2 - 8x + PR2
∴ PR2 = 9 - x2 + 8x — (i)
Now consider ΔPRS,
PS2 = PR2 + RS2
⇒ 32 = PR2 + x2
∴ PR2 = 9 - x2 — (ii)
By equating equation (i) and equation (ii) we get,
9 - x2 + 8x = 9 - x2
⇒ 8x = 0
⇒ x = 0
Now, put the value of x in equation (i)
PR2 = 9 - 02
⇒ PR = 3cm
∴ The length of the cord i.e. PQ = 2PR
So, PQ = 2 × 3 = 6cm.
Q2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Ans: Let AB and CD be two equal cords (i.e. AB = CD). In the above question, it is given that AB and CD intersect at a point, say, E.
It is now to be proven that the line segments AE = DE and CE = BE
Construction Steps:
Step 1: From the center of the circle, draw a perpendicular to AB i.e. OM ⊥ AB
Step 2: Similarly, draw ON ⊥ CD.
Step 3: Join OE. Now, the diagram is as follows-
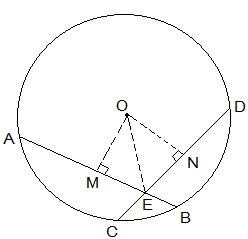 Proof:
Proof:From the diagram, it is seen that OM bisects AB and so, OM ⊥ AB
Similarly, ON bisects CD and so, ON ⊥ CD
It is known that AB = CD. So,
AM = ND — (i)
and MB = CN — (ii)
Now, triangles ΔOME and ΔONE are similar by RHS congruency since
∠OME = ∠ONE (They are perpendiculars)
OE = OE (It is the common side)
OM = ON (AB and CD are equal and so, they are equidistant from the centre)
∴ ΔOME≅ ΔONE
ME = EN (by CPCT) — (iii)
Now, from equations (i) and (ii) we get,
AM + ME = ND + EN
So, AE = ED
Now from equations (ii) and (iii) we get,
MB - ME = CN - EN
So, EB = CE (Hence proved).
Q3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Ans: From the question we know the following:
AB and CD are 2 chords which are intersecting at point E.
PQ is the diameter of the circle.
AB = CD.
Now, we will have to prove that BEQ = CEQ
For this, the following construction has to be done:
Construction:
Draw two perpendiculars are drawn as OM ⊥ AB and ON ⊥ D. Now, join OE. The constructed diagram will look as follows:
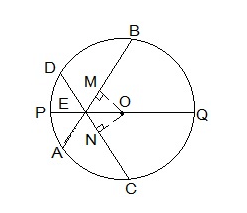 Now, consider the triangles ΔOEM and ΔOEN.
Now, consider the triangles ΔOEM and ΔOEN.Here,
OM = ON [Since the equal chords are always equidistant from the centre]
OE = OE [It is the common side]
∠OME = ∠ONE [These are the perpendiculars]
So, by RHS congruency criterion, ΔOEM ≅ ΔOEN.
Hence, by CPCT rule, MEO = NEO
∴ BEQ = CEQ (Hence proved).
Q4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig).
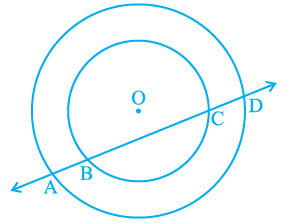 Ans: The given image is as follows:
Ans: The given image is as follows: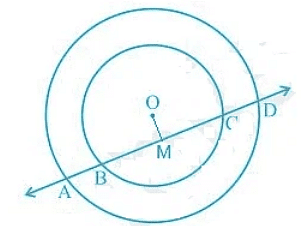 First, draw a line segment from O to AD such that OM ⊥ AD.
First, draw a line segment from O to AD such that OM ⊥ AD.So, now OM is bisecting AD since OM ⊥ AD.
Therefore, AM = MD — (i)
Also, since OM ⊥ BC, OM bisects BC.
Therefore, BM = MC — (ii)
From equation (i) and equation (ii),
AM - BM = MD - MC
∴ AB = CD.
Q5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Ans:
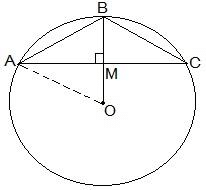 Let the positions of Reshma, Salma and Mandip be represented as A, B and C respectively.
Let the positions of Reshma, Salma and Mandip be represented as A, B and C respectively.From the question, we know that AB = BC = 6cm.
So, the radius of the circle i.e. OA = 5cm
Now, draw a perpendicular BM ⊥ AC.
Since AB = BC, ABC can be considered as an isosceles triangle. M is mid-point of AC. BM is the perpendicular bisector of AC and thus it passes through the centre of the circle.
Now,
let AM = y and
OM = x
So, BM will be = (5 - x).
By applying Pythagorean theorem in ΔOAM we get,
OA2 = OM2 +AM2
⇒ 52 = x2 +y2 — (i)
Again, by applying Pythagorean theorem in ΔAMB,
AB2 = BM2 +AM2
⇒ 62 = (5 - x)2 + y2 — (ii)
Subtracting equation (i) from equation (ii), we get
36 - 25 = (5 - x)2 + y2 - x2 - y2
Now, solving this equation we get the value of x as
x = 7 / 5
Substituting the value of x in equation (i), we get
y2 + (49 / 25) = 25
⇒ y2 = 25 – (49 / 25)
Solving it we get the value of y as
y = 24 / 5
Thus,
AC = 2 × AM
= 2 × y
= 2 × (24 / 5) m
AC = 9.6 m
So, the distance between Reshma and Mandip is 9.6 m.
Q6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Ans: First, draw a diagram according to the given statements. The diagram will look as follows.
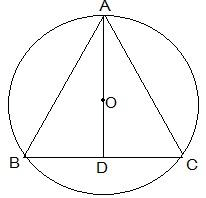 Here the positions of Ankur, Syed and David are represented as A, B and C respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.
Here the positions of Ankur, Syed and David are represented as A, B and C respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.AD ⊥ BC is drawn. Now, AD is median of ΔABC and it passes through the centre O.
Also, O is the centroid of the ΔABC. OA is the radius of the triangle.
OA = 2 / 3 AD
Let the side of a triangle a metres then BD = a / 2 m.
Applying Pythagoras theorem in ΔABD,
AB2 = BD2 + AD2
⇒ AD2 = AB2 - BD2
⇒ AD2 = a2 - (a / 2)2
⇒ AD2 = 3a2 / 4
⇒ AD = √3a / 2
OA = 2 / 3 AD
20 m = 2 / 3 × √3a / 2
a = 20√3 m
So, the length of the string of the toy is 20√3 m.
Exercise 9.3
Q1. In Fig, A, B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.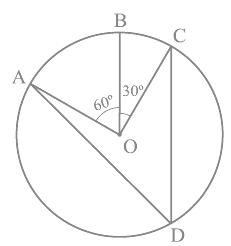
Ans: It is given that,
∠AOC = ∠AOB+∠BOC
So, ∠AOC = 60°+30°
∴ ∠AOC = 90°
It is known that an angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So,
∠ADC = (½)∠AOC
= (½)× 90° = 45°
Q2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Ans:
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle and the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Draw a circle with any radius and center O. Let AO and BO be the 2 radii of the circle and let AB be the chord equal to the length of the radius. Join them to form a triangle.
Here OA = OB = AB
Hence ∆ABO becomes an equilateral triangle.
Draw 2 points C and D on the circle such that they lie on the major arc and minor arc, respectively.
Since ∆ABO is an equilateral triangle, we get ∠AOB = 60°.
For the arc AB, ∠AOB = 2∠ACB as we know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
∠ACB = 1/2 ∠AOB = 1/2 × 60 = 30°
As you can notice the points A, B, C, and D lie on the circle. Hence ABCD is a cyclic quadrilateral.
We know that the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Therefore,
∠ACB + ∠ADB = 180°
30° + ∠ADB = 180°
∠ADB = 150°
So, when the chord of a circle is equal to the radius of the circle, the angle subtended by the chord at a point on the minor arc is 150° and also at a point on the major arc is 30°.
Q3. In Fig, ∠ PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠ OPR.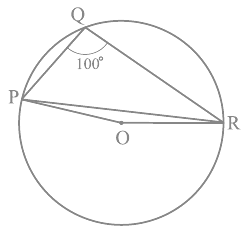
Ans: The angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So, the reflex ∠POR = 2×∠PQR
We know the values of angle PQR as 100°
So, ∠POR = 2×100° = 200°
∴ ∠POR = 360°-200° = 160°
Now, in ΔOPR,
OP and OR are the radii of the circle
So, OP = OR
Also, ∠OPR = ∠ORP
Now, we know the sum of the angles in a triangle is equal to 180 degrees
So,
∠POR+∠OPR+∠ORP = 180°
∠OPR+∠OPR = 180°-160°
As ∠OPR = ∠ORP
2∠OPR = 20°
Thus, ∠OPR = 10°
Q4. In Fig, ∠ ABC = 69°, ∠ ACB = 31°, find ∠ BDC.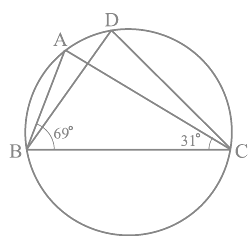
Ans: We know that angles in the segment of the circle are equal so,
∠BAC = ∠BDC
Now in the in ΔABC, the sum of all the interior angles will be 180°
So, ∠ABC + ∠BAC + ∠ACB = 180°
Now, by putting the values,
∠BAC = 180° - 69° - 31°
So, ∠BAC = 80°
∴ ∠BDC = 80°.
Q5. In Fig, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠ BAC.
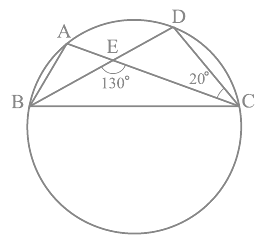
Ans: We know that the angles in the segment of the circle are equal.
So,
∠ BAC = ∠ CDE
Now, by using the exterior angles property of the triangle
In ΔCDE we get,
∠ CEB = ∠ CDE + ∠ DCE
We know that ∠ DCE is equal to 20°
So, ∠ CDE = 110°
∠ BAC and ∠ CDE are equal
∴ ∠ BAC = 110°.
Q6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.
Ans: Consider the following diagram.Consider the chord CD,
We know that angles in the same segment are equal.
So, ∠ CBD = ∠ CAD
∴ ∠ CAD = 70°
Now, ∠ BAD will be equal to the sum of angles BAC and CAD.
So, ∠ BAD = ∠ BAC + ∠ CAD
= 30° + 70°
∴ ∠ BAD = 100°
We know that the opposite angles of a cyclic quadrilateral sums up to 180 degrees.
So,
∠ BCD + ∠ BAD = 180°
It is known that ∠ BAD = 100°
So, ∠ BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠ BCA = ∠ CAB (They are the angles opposite to equal sides of a triangle)
∠ BCA = 30°
also, ∠ BCD = 80°
∠ BCA + ∠ ACD = 80°
Thus, ∠ ACD = 50° and ∠ ECD = 50°.
Q7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Ans: Given:
1. The diagonals of the cyclic quadrilateral are diameters of the circle.
2. The quadrilateral is cyclic (its vertices lie on the circle).
Proof:
A diameter of a circle subtends a 90∘ angle on the circumference of the circle (by the property of a semicircle).
Let the cyclic quadrilateral be ABCD, and let the diagonals AC and BD be the diameters of the circle.
Since AC is a diameter:
∠ABC=90∘ and ∠ADC=90∘(Both ∠ABC and ∠ADC are subtended by AC on opposite sides of the circle).
Similarly, since BD is a diameter:
∠BAD = 90∘ and ∠BCD = 90∘ (Both ∠BAD and ∠BCD are subtended by BD).
From the above, all four angles of the quadrilateral ABCD are 90∘. Hence, ABCD is a quadrilateral where:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90∘
Q8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Ans: Construction:
Consider a trapezium ABCD with AB ║CD and BC = AD.
Draw AM ⊥ CD and BN ⊥ CD.
In ΔAMD and ΔBNC,
The diagram will look as follows:In ΔAMD and ΔBNC,
AD = BC (Given)
∠AMD = ∠BCN (By construction, each is 90º)
AM = BN (Perpendicular distance between two parallel lines is same)
ΔAMD ≅ ΔBNC (RHS congruence rule)
∠ADC = ∠BCD (CPCT)...(1)
∠BAD and ∠ADC = 180º....(2) [Sum of the co-interior angles]
∠BAD and ∠BCD = 180º [Using equation (1)]
This equation shows that the opposite angle are supplementary.
Therefore, ABCD is a cyclic quadrilateral.
Q9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig). Prove that ∠ACP = ∠ QCD.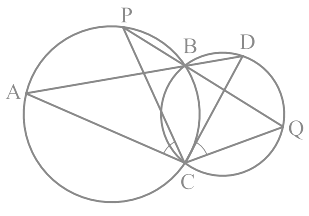
Ans: Construction:
Join the chords AP and DQ.
For chord AP, we know that angles in the same segment are equal.
So, ∠ PBA = ∠ ACP ......(i)
Similarly for chord DQ,
∠ DBQ = ∠ QCD .....(ii)
It is known that ABD and PBQ are two line segments which are intersecting at B.
At B, the vertically opposite angles will be equal.
∴ ∠ PBA = ∠ DBQ ......(iii)
From equation (i), equation (ii) and equation (iii) we get,
∠ ACP = ∠ QCD.
Q10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Ans: First draw a triangle ABC and then two circles having diameter as AB and AC respectively.
We will have to now prove that D lies on BC and BDC is a straight line.Proof:
We know that angle in the semi-circle are equal
So, ∠ ADB = ∠ ADC = 90°
Hence, ∠ ADB + ∠ ADC = 180°
∴ ∠ BDC is straight line.
So, it can be said that D lies on the line BC.
Q11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Ans: We know that AC is the common hypotenuse and ∠ B = ∠ D = 90°.
Now, it has to be proven that ∠ CAD = ∠ CBDSince, ∠ ABC and ∠ ADC are 90°, it can be said that They lie in the semi-circle.
So, triangles ABC and ADC are in the semi-circle and the points A, B, C and D are concyclic.
Hence, CD is the chord of the circle with center O.
We know that the angles which are in the same segment of the circle are equal.
∴ ∠ CAD = ∠ CBD
Q12. Prove that a cyclic parallelogram is a rectangle.
Ans: It is given that ABCD is a cyclic parallelogram and we will have to prove that ABCD is a rectangle.
Proof:
Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180º (Opposite angles of a cyclic quadrilateral)....(1)
We know that opposite angles of a parallelogram are equal.
∠A = ∠C and ∠B = ∠D
From equation (1),
∠A + ∠C = 180º
∠A + ∠A = 180º
2∠A = 180º
∠A = 90°
Parallelogram ABCD has one of its interior angles as 90º.
Thus, ABCD is a rectangle.
|
40 videos|566 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 - Maths Circles Exercise 9.1
| 1. What is the formula for the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How do you calculate the length of an arc in a circle? |  |
| 5. What is the significance of a tangent to a circle? |  |