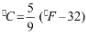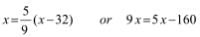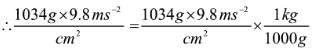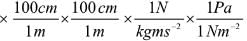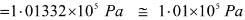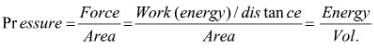Nature of Matter, Scientific Notation and Units & Dimensional Analysis | Additional Study Material for JEE PDF Download
Nature of Matter
Introduction
Anything that exhibits inertia is known as matter. The quantity of matter is its mass. Example: chalk table. In simple language, anything which has mass and occupies space is called matter.
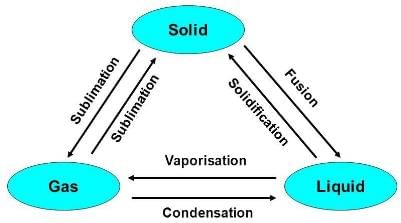
Matter can exist in three physical states viz. solid, liquid, and gas.
The constituent particles of matter in these three states can be represented as shown in the figure: A Representation of the Solid, Liquid, and Gas States
A Representation of the Solid, Liquid, and Gas States
- In solids, these particles are held very close to each other in an orderly fashion and there is not much freedom of movement.
- In liquids, the particles are close to each other but they can move around.
- In gases, the particles are far apart as compared to those present in solid or liquid states and their movement is easy and fast.
Because of such an arrangement of particles, different states of matter exhibit the following characteristics:
- Solids have definite volume and definite shape.
- Liquids have a definite volume but not a definite shape. They take the shape of the container in which they are placed.
- Gases have neither a definite volume nor a definite shape. They completely occupy the container in which they are placed.
Note: These three states of matter are interconvertible by changing the conditions of temperature and pressure.
Classification of Matter (At Macroscopic/Bulk Level)
This classification of matter is based upon the chemical composition of various substances. According to this matter can be further divided into two types, pure substance, and mixture.
Mixtures are also of two types, homogenous mixtures and heterogeneous mixtures.
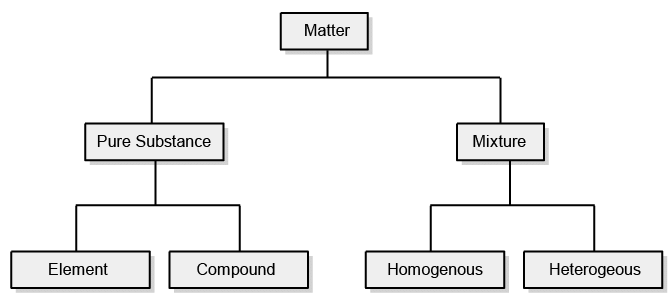 Classification of Matter
Classification of Matter
➢ Elements
- The primary stuff present in all the substances is known as an element, whose smallest unit is known as an atom.
- Sodium, copper, silver, hydrogen, oxygen, etc. are some examples of elements. They all contain atoms of one type. However, the atoms of different elements are different in nature.
- Total 118 elements are known till the date of which 92 are naturally occurring elements rest are results of artificial transmutation. There are 88 metals, 18 nonmetals, and 6 metalloids.
- A non-elemental pure substance is called a compound in which more than one atom of elements is linked by chemical bonds formed due to chemical reaction.
- The resulting molecule is an electrically neutral particle of constant continuous composition.
➢ Mixture
- Mixtures are the aggregate of more than one type of pure substance whose chemical identity remains maintained even in mixtures. Their constituent ratio may vary, unlike compounds.
Example: Sugar + Water = Sugar Syrup
Gunpowder: 75% KNO3 + 10% Sulphur + 15% carbon
There are two types of mixture:
(a) Homogeneous
(b) Heterogenous
- Homogeneous mixtures are those whose composition for each part remains constant.
Example: aqueous and gaseous solution. - Heterogeneous mixtures are those whose composition may vary for each and every part.
Example: soil, concrete mixtures.
Table: Comparison between Homogeneous and Heterogeneous mixtures
Table: Comparison between Compound and Mixtures
Try Yourself!
Scientific Notation, Precision & Accuracy
Uncertainty in Measurement
Many times in the study of chemistry, one has to deal with experimental data as well as theoretical calculations.
There are meaningful ways to handle the numbers conveniently and present the data realistically with certainty to the extent possible like:
- Scientific Notation
- Significant Figures
- Dimension Analysis
➢ Scientific Notation
- Scientific Notation is a way of expressing numbers that are too big or too small to be conveniently written in decimal form.
- In which any number can be represented in form N × 10n (where n is an exponent having positive or negative values and N can vary between 1 to 10).
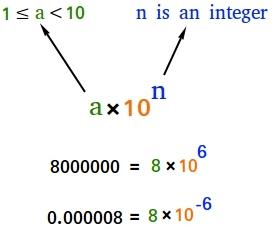 Scientific Notation
Scientific Notation
Example: We can write 232.508 as 2.32508 × 102 in scientific notation. Similarly, 0.00016 can be written as 1.6 × 10–4.
Thus, we can write 232.508 as 2.32508 × 102 in scientific notation. Note that while writing it, the decimal had to be moved to the left by two places and the same is the exponent (2) of 10 in the scientific notation.
Similarly, 0.00016 can be written as 1.6 × 10–4. Here the decimal has to be moved four places to the right and (– 4) is the exponent in the scientific notation.
➢ Multiplication and Division for Exponential Numbers
- These two operations follow the same rules which are there for exponential numbers, i.e.
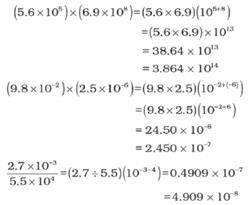
➢ Addition and Subtraction for Exponential Numbers
- For these two operations, first the numbers are written in such a way that they have the same exponent. After that, the coefficients (digit terms) are added or subtracted as the case may be.
- Thus, for adding 6.65 × 104 and 8.95 × 103, exponent is made same for both the numbers. Thus, we get (6.65 × 104) + (0.895 × 104).
Precision and Accuracy
- Every experimental measurement has some amount of uncertainty associated with it. However, one would always like the results to be precise and accurate. Precision and accuracy are often referred to while we talk about the measurement.
- Accuracy refers to the closeness of a measured value to a standard or known value.
Example: If in lab you obtain a weight measurement of 3.2 kg for a given substance, but the actual or known weight is 10 kg, then your measurement is not accurate. In this case, your measurement is not close to the known value. - Precision refers to the closeness of two or more measurements to each other.
Using the example above, if you weigh a given substance five times, and get 3.2 kg each time, then your measurement is very precise. Precision is independent of accuracy. - You can be very precise but inaccurate, as described above. You can also be accurate but imprecise.
Example: If on average, your measurements for a given substance are close to the known value, but the measurements are far from each other, then you have accuracy without precision.
Example: If the true value for a result is 2.00 g.
(a) Student ‘A’ takes two measurements and reports the results as 1.95 g and 1.93 g.
These values are precise as they are close to each other but are not accurate.
(b) Another student repeats the experiment and obtains 1.94 g and 2.05 g as the results for two measurements.
These observations are neither precise nor accurate.
(c) When a third student repeats these measurements and reports 2.01g and 1.99 g as the result.
These values are both precise and accurate.
Examples:
Q.1. Which of the following options is not correct?
(a) 8008 = 8.008 x 103
(b) 208 = 3
(c) 5000 = 5.0 x 103
(d) 2.0034 = 4
Ans: (d)
Solution:
2.0034 = 4
Q.2. Exponential notation in which any number can be represented in the form, Nx 10n here N is termed as
(a) non –digit term
(b) digit term
(c) numeral
(d) base term
Ans: (b)
Solution:
In exponential notation N × 10n, N is a number called digit term which varies between 1.000 and 9.000….
Q.3. In scientific notation,0.00016 can be written as
(a) 1.6 x 10-4
(b) 1.6 x 10-3
(c) 1.6 x 10-2
(d) 1.6 x 10-1
Ans: (a)
Solution:
0.00016 can be written as 1.6 × 10-4 in scientific notation
4. Addition of 6.65 x 104 and 8.95 x 103, in terms of scientific notation will be
(a) 7.545 104
(b) 75.45 10 3
(c) 754.5 102
(d) 75.45 100
Ans: (a)
Solution:
6.65 × 104 + 8.95 × 103
= (6.65 + 0.895) × 104 = 7.545 × 104
Q.5. The substraction of two numbers
2.5 x 10-2 -4.8 x 10 -3 gives the following value.
(a) 2.02 x 10-3
(b) 2.02 x 10-2
(c) 2.02 x 10-1
(d) 2.02 x 100
Ans: (b)
Solution:
2.5 × 10-2 - 4.8 × 10-3
= 2.5 × 10-2 — (0.48 × 10-2) = 2.02 × 10-2
Q.6. A refers to the closeness of various measurements for the same quantity. B is the agreement of a particular value to the true value of the result. A and B respective are
(a) A → Significant figures, B → accuracy
(b) A → accuracy, B → precision
(c) A → Precision, B → accuracy
(d) A → significant figures, → precision
Ans: (c)
Q.7. Which of the following statement is/are true?
(a) Every experimental measurement has zero amount of uncertainty associated with it
(b) One would always like the result to be precise and accurate
(c) Precision and accuracy are often referred to while we talk about the measurement
(d) Both (b) and (c)
Ans: (d)
Solution: Every experimental measurement has some amount of uncertainty associated with it.
Try Yourself!
Units & Dimensional Analysis
Conversion of Units
- The simplest way to carry out calculations that involve different units is to use dimensional analysis. The simplest way to carry out calculations that involve different units is to use dimensional analysis.
- As there is a need to convert units from one system to the other. The method used to accomplish this is called the factor label method or unit factor method or dimensional analysis.
- In this method a quantity expressed in one unit is converted into an equivalent quantity with a different unit by using a conversion factor which express the relationship between units:

- This is based on the fact that ratio of each fundamental quantity in one unit with their equivalent quantity in other unit is equal to one For example, in case of mass
1 kg = 2.205 pound = 1000 gm - In this way any derived unit first expressed in dimension and each fundamental quantity like mass length time are converted in other system of desired unit to work out the conversion factor.
Example: How unit of work / energy i.e. joule, in S.I. system is related with unit erg in C.G.S system?
Dimension of work = force x displacement = MLT-2 × L = ML2T-2
1 joule = 1 kg (1 metre)2 × (1sec)-2
⇒ 1 × Kg × 1000 gm/1Kg × [1 metre × 100 cm/1 metre] × [1 sec]-2
⇒ 100 gm × (100)2 × 1 em2 × (1 sec)-2
⇒ 1000 × 10000 × 1 gm × 1 cm2 × 1 sec-1
⇒ 1 joule = 107 erg
Similarly, we can deduce other conversion factor for other quantity in different unit by the dimensional analysis method.
Another interesting example is the conversion of liter – atmosphere to joule (the SI unit of energy) by multiplying with two successive unit factors.
Thus,
1 L atm × (10-3 m3/1L) × 101.325 Pa/1 atm
= 101. 325 Pa M3
Knowing that Pa = N/m2,
we can write
101.325 Pa m3 = 101.325 (N/m2) m3
= 101.325 N m = 101.325 J
Hence, 1 L atm = 101.325 J
➢ Mass and Weight
- Mass of a substance is the amount of matter present in it while weight is the force exerted by gravity on an object.
- The mass of a substance is constant whereas its weight may vary from one place to another due to change in gravity. The mass of a substance can be determined very accurately by using an analytical balance.
➢ Volume
- Volume has the units of (length)3. So, volume has units of m3 or cm3 or dm3. A common unit, litre (L) is not an SI unit, is used for measurement of volume of liquids.
1 L = 1000 mL, 1000 cm3 = 1 dm3
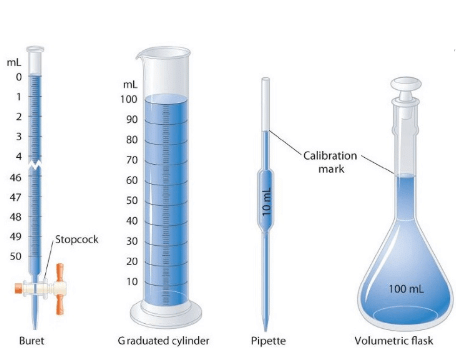 Some Volume Measuring Devices
Some Volume Measuring Devices
➢ Density
- Density of a substance is its amount of mass per unit volume. SI unit of density = SI unit of mass/SI unit of volume = kg/m3 or kg m–3.
- This unit is quite large and a chemist often expresses density in g cm–3.
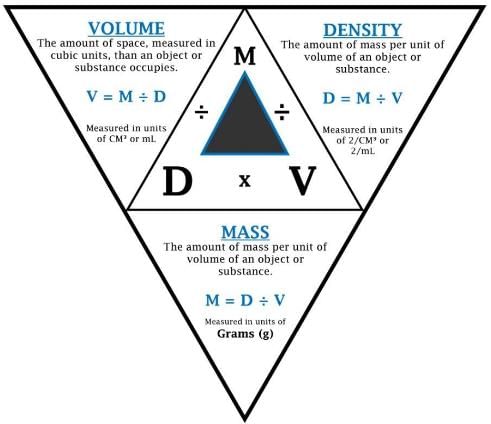 Relationship between Density, Mass and Volume
Relationship between Density, Mass and Volume
➢ Temperature
There are three common scales to measure temperature:
1. °C (degree Celsius)
2. °F (degree Fahrenheit)
3. K (kelvin)
Here, K is the SI unit.
Conversion Formulas:
- K = °C + 273.15
- °F = (9/5) °C +32
Note: Temperature below 0 °C (i.e. negative values) are possible in the Celsius scale but in the Kelvin scale, the negative temperature is not possible.
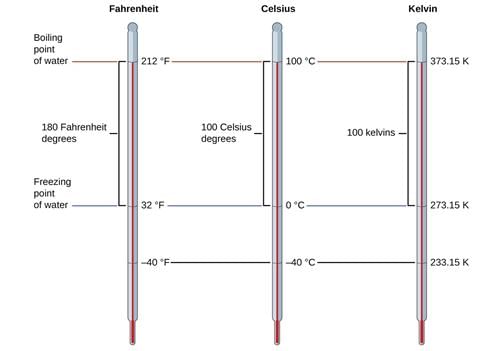 Temperature Kelvin scale
Temperature Kelvin scale
Example 1. What is the mass of 1 L of mercury in grams and in kilograms if the density of liquid mercury is 13.6 g cm−3?
Solution. We know the relationship, 1 L = 1000 cm3 and
Also, density = mass/volume
We can write, mass = (volume) (density)
Therefore, the mass of 1 L of mercury is equal to
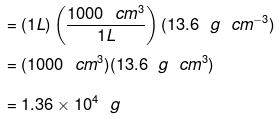
The mass in kilograms can be calculated as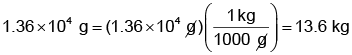
(Remember,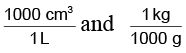
are conversion factors with which we have to multiply for getting our answer in appropriate units).
Example 2. How unit of velocity i.e. kilometer/hour is related to unit meter/second.
Solution. We know the relationship, velocity = total displacement/total time
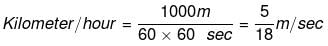
Prefixes in S.I. system
Name | Symbol | Quantity |
yotta | Y | 1024 |
zetta | Z | 1021 |
exa | E | 1018 |
peta | P | 1015 |
tera | T | 1012 |
giga | G | 109 |
mega | M | 106 |
kilo | k | 103 |
hecto | h | 102 |
deca | da | 10 |
deci | d | 10-1 |
centi | c | 10-2 |
miIIi | m | 10-3 |
micro | M | 10-6 |
nano | n | 10-9 |
pico | P | 10-12 |
fempto | f | 10-15 |
atto | a | 10-18 |
zepto | z | 10-21 |
yocto | y | 10-24 |
Try Yourself!
1Pa = 1Nm-2
If the mass of air at sea level is 1034 g cm-2, the pressure in pascal is
|
22 videos|163 docs|17 tests
|