Network Theory - Passive Elements | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Some Passive Elements |

|
| Resistor |

|
| Inductor |

|
| Capacitor |

|
Passive elements in electrical and electronic circuits are components that do not generate energy but can store or dissipate it. They typically do not require an external power source to operate and can only absorb energy. The most common passive elements include resistors, capacitors, and inductors.
Some Passive Elements
Hence, some of the common passive elements are:
- Resistor
- Inductor
- Capacitor
- Coil
Resistor
- The main functionality of Resistor is either opposes or restricts the flow of electric current. Hence, the resistors are used in order to limit the amount of current flow and / or dividing (sharing) voltage.
- Let the current flowing through the resistor is I amperes and the voltage across it is V volts. The symbol of resistor along with current, I and voltage, V are shown in the following figure.
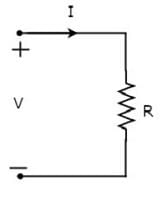 R in the given circuit is resistor
R in the given circuit is resistor
According to Ohm’s law, the voltage across resistor is the product of current flowing through it and the resistance of that resistor. Mathematically, it can be represented as:
⇒ V= IR Equation 1
⇒ I= V/R Equation 2Where, R is the resistance of a resistor.
From Equation 2, we can conclude that the current flowing through the resistor is directly proportional to the applied voltage across resistor and inversely proportional to the resistance of resistor.
Power in an electric circuit element can be represented as
P = VI Equation 3
Substitute, Equation 1 in Equation 3.
⇒ P = (IR)*I
⇒ P = I2R Equation 4
Substitute, Equation 2 in Equation 3.
Equation 5
So, we can calculate the amount of power dissipated in the resistor by using one of the formulae mentioned in Equations 3 to 5.
Inductor
In general, inductors will have number of turns. Hence, they produce magnetic flux when current flows through it. So, the amount of total magnetic flux produced by an inductor depends on the current, I flowing through it and they have linear relationship.
Mathematically, it can be written as:
⇒ Ψ α I
⇒ Ψ = LI
Where,
- Ψ is the total magnetic flux
- L is the inductance of an inductor
Let the current flowing through the inductor is I amperes and the voltage across it is V volts. The symbol of inductor along with current I and voltage V are shown in the following figure.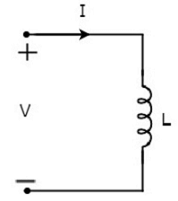 L is the inductor in the circuitAccording to Faraday’s law, the voltage across the inductor can be written as
L is the inductor in the circuitAccording to Faraday’s law, the voltage across the inductor can be written as
Substitute Ψ = LI in the above equation.
From the above equations, we can conclude that there exists a linear relationship between voltage across inductor and current flowing through it.
We know that power in an electric circuit element can be represented as
P = VI
Substitute in the above equation.
By integrating the above equation, we will get the energy stored in an inductor as
So, the inductor stores the energy in the form of magnetic field.
Capacitor
- In general, a capacitor has two conducting plates, separated by a dielectric medium. If positive voltage is applied across the capacitor, then it stores positive charge.
- Similarly, if negative voltage is applied across the capacitor, then it stores negative charge.
So, the amount of charge stored in the capacitor depends on the applied voltage V across it and they have linear relationship.
Mathematically, it can be written as:
⇒ Q α V
⇒ Q = CV
Where,
- Q is the charge stored in the capacitor.
- C is the capacitance of a capacitor.
Let the current flowing through the capacitor is I amperes and the voltage across it is V volts. The symbol of capacitor along with current I and voltage V are shown in the following figure.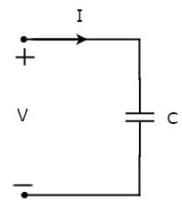
We know that the current is nothing but the time rate of flow of charge. Mathematically, it can be represented as
I = dQ/dt
Substitute Q = CV in the above equation.
From the above equations, we can conclude that there exists a linear relationship between voltage across capacitor and current flowing through it.
We know that power in an electric circuit element can be represented as
P = VI
Substitute in the above equation.
By integrating the above equation, we will get the energy stored in the capacitor as
So, the capacitor stores the energy in the form of electric field.
|
76 videos|152 docs|62 tests
|
FAQs on Network Theory - Passive Elements - Network Theory (Electric Circuits) - Electrical Engineering (EE)
| 1. What are passive elements in electrical engineering? |  |
| 2. What is the function of a resistor in a circuit? |  |
| 3. How does an inductor work in a circuit? |  |
| 4. What is the role of a capacitor in an electrical circuit? |  |
| 5. Can passive elements be used in combination to create more complex circuits? |  |
















