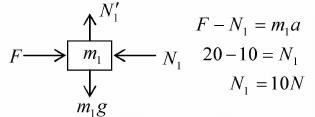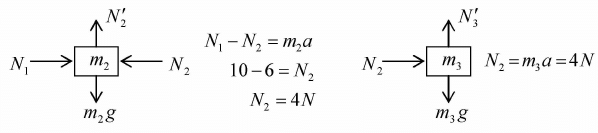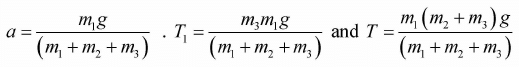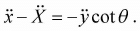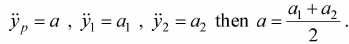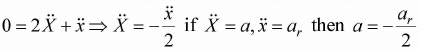Newton’s Laws of Motion & Free Body Diagram | Mechanics & General Properties of Matter - Physics PDF Download
Newton's Laws of Motion
Three physical laws laid the foundation of classical mechanics. They describe the relationship between a body and the forces acting upon it and its motion in response to those forces.
First Law (Law of Inertia)
Inertia is an inherent property of matter that always opposes the change of its state. In general mass is measure of inertia. Heavier the mass greater is the inertia. Inertial frame is a coordinate system with a clock attached that moves with a constant speed.
In the absence of an external force in the inertial frame an object either remains at rest or
continues to move at a constant velocity.
According to first law if net force (the vector sum of all forces acting on an object) is zero, then the momentum of the object is constant (Both magnitude and direction). So, the first law can be mathematically stated as 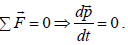
Second Law
The second law states that the net force on an object is equal to the rate of change (that is, the derivative) of its linear momentum 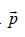 in an inertial reference frame i.e.
in an inertial reference frame i.e.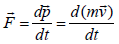
If the mass is constant then the vector sum of the external forces 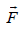 on an object is equal to the mass m of that object multiplied by the acceleration vector
on an object is equal to the mass m of that object multiplied by the acceleration vector 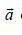 of the object
of the object 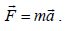
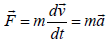
One can visualize Newton’s second law as cause and effect phenomenon where external force is equivalent to cause and resulting acceleration is its effect which is measured by a force.
In the case when the velocity is very high (close to velocity of light) Newton’s law should be modified according to special theory of relativity.
Third Law
To every action there is an equal and opposite reaction. The action and reaction acts on two different bodies. Consider two bodies body one exerts a force 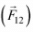 on second body and the second body simultaneously exerts a force
on second body and the second body simultaneously exerts a force  equal in magnitude and opposite in direction on the first body i.e.
equal in magnitude and opposite in direction on the first body i.e. 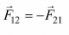
Impulse
An impulse 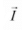 occurs when a force
occurs when a force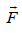 Facts over a short interval of time Δt(Δt → 0) and it is given by
Facts over a short interval of time Δt(Δt → 0) and it is given by  . Since the force is the time derivative of momentum it follows that
. Since the force is the time derivative of momentum it follows that  when mass is constant
when mass is constant 
Equation of Motion
The equation of motion is given by ∑Fx - max,∑Fy = may. Number of equations must be equal to the number of unknown variables so that one can solve them for complete as well unique solution.
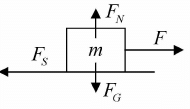
Free Body Diagram
The Free body diagram (FBD) is representation of all forces acting on independent bodies. To draw FBD we assume the body to be a point mass and then we mark all forces acting on it. A suitable coordinate axis may be drawn to resolve the forces along X and Y direction.
Some common external forces are discussed below:
1. Weight: The weight of body is w = mg . The w eight o f the body is always vertically downward as shown in figure.
 2. Normal forces: When a body is in contact with any surface then the surface will exert normal force N (reaction force). The direction of normal force is perpendicular to the plane of surface.
2. Normal forces: When a body is in contact with any surface then the surface will exert normal force N (reaction force). The direction of normal force is perpendicular to the plane of surface.
If a Block of mass m is lying on any surface, the surface will push the block in perpendicular direction w.r.t. the plane of the surface with magnitude N and at the same time by Newton’s third law the block will push the contact surface with same magnitude but opposite in direction.
Example 1: A Force F of 20N acts on a block m1 = 5kg such that m2 = 3kg is in contact with m1 and m3 = 2kg as shown in figure.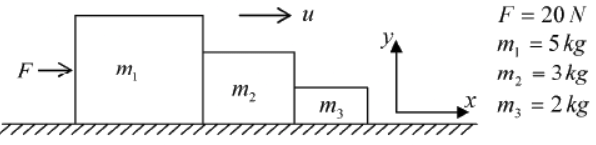
(i) Find acceleration of each block
(ii) Find contact force in each block
(i) All are moving with same acceleration
F = (m1 + m2 + m3) a ⇒ a = 2m/sec2
(ii) Free body diagram
3. Tension: Force F is exerted on mass m through string .Then any section of the string is pulled by two equal and opposite forces. Any one of these forces is called tension. Tension always gives pulling effect to mass. In the figure, the force F is acted on mass m through string so there is tension T in the string giving pulling effect.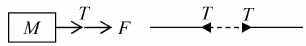
Now let us analyze another system in which two masses mx and m2 are attached with a string and force F is acted on the mass mx as shown in figure. Due to force F tension T is developed in the string. If one will draw free body diagram for mx the tension will act towards left and if free body diagram draw for m2 the tension will act towards right. In both the case tension will produce pulling effect on mass mx and m2.
Different forces shown in figure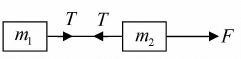 String is massless show there is same tension acts on is part of the string. Free body diagram for mass mx and m2
String is massless show there is same tension acts on is part of the string. Free body diagram for mass mx and m2
If the rope is massless the tension in string is same for all sections of string other wise it will depend on mass of segment of the rope.
Example 2: Figure shows a block of mass m1 and m2 attached to m ass less string. Another mass m3 Attached to mass m2 with different mass less string. All contact surface are Smooth. Mass m2 can move vertical downward direction under influence of Gravitation field g . Find the acceleration of each mass and tension in both string.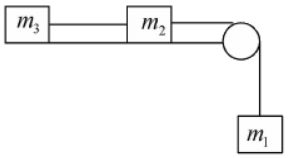
All forces act on the system shown in figure T and T1 are Tension in first and second string. m1g is weight of mass mx. The weight of other particle will balanced with their normal force exerted by the surface. Hence length of each string is fixed so all three particle will move will same
Acceleration: The free body diagram and equation of motion for mass m1
Solving equation (1) (2) and (3) simultaneously one can get
4. Friction: In general, frictional force is force which is responsible to oppose the relative motion between two surfaces. It is of two types: Static Friction: When no relative motion exists between two contact surfaces after application of a force, the force along the surface and opposite to the direction in which the motion tends to take place is known as static friction. For Example when a box is placed on the floor of a truck and the truck accelerates the box moves with the truck (remaining at rest relative to the truck). It is the force of static friction that acts on the box to prevent it from sliding along the surface of the truck. To determine the direction of the force of static friction, think about the motion that would result if there were no friction then decide in which direction relative motion will take place, the static friction will be oppose to the relative motion between contact surfaces.
For example to start a walk one should push back his foot on the floor. If there were no friction the foot will slide back. Static friction opposes this motion and thus is directed in forward direction.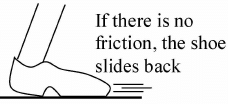 On a frictionless floor, your shoe slides backward over the floor when you try to walk forward (a).
On a frictionless floor, your shoe slides backward over the floor when you try to walk forward (a). Static friction opposes this motion, so the static force of friction, applied by the ground on you, is directed forward (b).The static force of friction opposes the relative motion that would occur if there were no friction. Another interesting feature is that the static force of friction adjusts itself to whatever it needs to be to prevent relative motion between the surfaces in contact. Within limits the static force of friction has a maximum value, Fs max, and the coefficient of static friction jus is defined in terms of this maximum value:
Static friction opposes this motion, so the static force of friction, applied by the ground on you, is directed forward (b).The static force of friction opposes the relative motion that would occur if there were no friction. Another interesting feature is that the static force of friction adjusts itself to whatever it needs to be to prevent relative motion between the surfaces in contact. Within limits the static force of friction has a maximum value, Fs max, and the coefficient of static friction jus is defined in terms of this maximum value: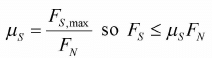 where FN is normal force on the block
where FN is normal force on the block
Key ideas for static friction: The static force o f friction is whatever is required to prevent relative motion between surfaces in contact. The static force of friction is adjustable only up to a point. If the required force exceeds the maximum value FS,max = μs Fn ,then relative motion will occur then kinetic friction will apply which is equivalent to μkN
Kinetic Friction: If there is relative speed between surface and mass m then frictional force is identifying as fk = μN where μ is coefficient of kinetic friction and TV is norm al force. The direction of / is directed opposite to the relative motion between block and friction.
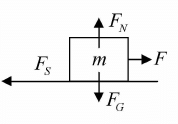
Example 3: Let us now explore a situation that involves the adjustable nature of the force of static friction. A box with a weight of mg = 40 N is at rest on a floor. The coefficient of static friction between the box and the floor is μs = 0.50 , while the coefficient of kinetic friction between the box and the floor is μK = 0.40.
Step 1 - What is the force of friction acting on the box if you exert no force on the box?
Let’s draw a free-body diagram of the box (see figure) as it sits at rest. Because the box remains at rest, its acceleration is zero and the forces must balance. Applying Newton’s Second Law tells us that FN = mg = 40 N. There is no tendency for the box to move, so there is no force of friction.Step 2 - What is the force of friction acting on the box if you push horizontally on the box with a force of 10N, as in Figure?
Nothing has changed vertically, so we still have FN = mg = 40 N. To determine whether or not the box will move we determine the maximum 4- possible force of static friction in this case.Fs < μsFn = 0.50 x 40 N = 20 N
The role of static friction is to keep the box at rest. If we exert a horizontal force of 10 N on the box, the force of static friction acting on the box must be 10 A in the opposite direction, to keep the box from moving. The free-body diagram for the present situation is shown in Figure. 10 N is below the 20 N (maximum value) so the box will not move.
Step 3 - What is the force of friction acting on the box if you increase your force to 15 N?This situation is similar to step 2. Now, the force of static friction adjusts itself to 15 N in the opposite direction of your 15 N force. 15 N is still less than the maximum possible force of static friction (20 N), so the box does not move.
Step 4 - What is the force of friction acting on the box if you increase your force to 20 N?
If your force is 20 N, the force of static friction matches you with 20 N in the opposite direction. We are now at the maximum possible value of the box move.Step 5 - What is the force of friction acting on the box if you increase your force to 25 N?
Increasing your force to 25 N (which is larger in magnitude than the maximum possible force of static friction) makes the box move.F = μk FN = 0 .40 x 40 N = 16 N
Example 4: Block and Wedge with Friction A block of mass m rests on a fixed wedge at an angle θ and the coefficient of friction is μ. (For wooden blocks, μ is of the order of 0.2 to 0.5). Find the value of 6 at which the block starts to slide.
In the absence of friction the block would slide down the plane hence the friction force f is in upward direction.
With the coordinates shown the equation of motion is given by
= W sin 6 - f and
= N - W cos θ = 0 when sliding starts. f has its maximum value μN , and
The equation then give
W sin θmax = μN And Wcosθmax = N
Hence, tanθmax = μ
Notice that as the wedge angle is gradually increased from zero, the friction force grows in magnitude from zero toward its maximum value μN since before the block begins to slide we have f = W sinθ, θ < θmax
Example 5: A block of mass m kept on the surface of another block of mass M. There is friction between the surfaces of two blocks. Find the direction of frictional force on both blocks.
Case 1: Two block move together when force F is applied on block M as shown in figure.
(a) No relative speed between blocks M and m.
(b) If no friction was there between block m and M then block M will move in direction of applied force and the block m will move opposite to the block M.
(c) The frictional force on block m will be in the direction of force F and due to Newton’s third law frictional force on block M will in opposite direction of applied force F as shown in figure.
Case 2: Two block move together where force F is applied on block M as shown in figure(a) No relative speed between blocks M and m.
(b) If no friction was there between block m and M then block m will move in direction of applied force and the block M will move opposite to the block m.
(c) The frictional force on block M will be in the direction of force F and due to Newton’s third law frictional force on block m will in opposite direction of applied force F as shown in figure.
Case 3: The force is applied on block M and block and block m is moving with velocity v1 In same direction of force F. The mass m is speedspeed with respect to block M
If block m is moving with speed v1 with respect to block in a direction of force F then frictional force on block m will in opposite direction of v1 and block M is moving with respect to mass m in the opposite direction of force F so frictional force on mass M is in same direction of force F.
Case 4: The force is applied on block m and block M is moving with velocity v2 in same direction of force.If block M is moving with speed v2 with respect to block in a direction of force F then frictional force on block M will in opposite direction of v2 and block m is moving with respect to mass M in the opposite direction of force F so frictional force on mass M is in same direction of force F
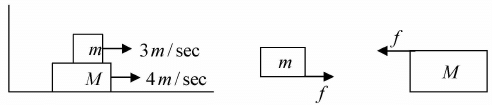
Case 5: Both blocks m and M moving with speed 3w/sec and 4w/sec respectively moving with respect to ground.In this case block m and mass M is moving with respect to ground in same direction lets say positive x direction. The speed of block m with respect to block M is 3m/sec-4m/sec = -1m/sec which means block m is moving in negative x direction so frictional force is in positive x direction.
Similarly, block M is moving with respect to block m with speed 4m/sec - 3m/sec = 1m/sec, which means block M is moving in positive x direction with respect to block m so frictional force is in negative x direction.
5. Pseudo Force: In a situation where the observer is on accelerated frame of reference, the observer will measure acceleration on another mass without any external force. This invalidate Newton’s law of motion. So the concept of pseudo force is introduced to modify Newton’s equations for accelerated frames. If a0 is acceleration of observer and he measures the pseudo force Fs on rest mass m , the magnitude of pseudo Fs = ma0 and its direction is opposite to direction of observer.
Let us understand the concept of pseudo force from following example:
Consider two observers A and B moving with acceleration 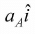 and
and  respectively with respect to mass m then observer A measure pseudo force maA in
respectively with respect to mass m then observer A measure pseudo force maA in 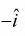 direction and observer B measure pseudo force maB in
direction and observer B measure pseudo force maB in 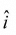 directions respectively. Concept of pseudo force makes Newton’s laws and motion valid in non-inertial frames.
directions respectively. Concept of pseudo force makes Newton’s laws and motion valid in non-inertial frames.
Example 6: A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
The situation is shown in figure Suppose the mass of the bob is m and the string makes an angle θ with the vertical. We shall work from the car frame. This frame is noninertial as it has an acceleration
with respect to an inertial frame (the road). Observer attached to car will observe pseudo force ma0 on the bob of pendulum which is in opposite direction of acceleration of car.
Take the bob as the system.
The forces are:
(a) T along the string, by the string
(b) mg downward, by the earth
(c) ma0 towards left (pseudo force).The free body diagram is shown in figure. As the bob is at rest (remember we are discussing the motion with respect to the car) the force in (a),(b) and (c) should add to zero. Take X - axis along the forward horizontal direction and Y -axis along the upward vertical direction. The components of the forces along the X - axis give
T sin θ - m a0 = 0 or T sin θ = ma0 (i)
and the components along the Y -axis give
T cos θ - mg = 0 or T cosθ = mg. (ii)
Dividing (i) by (ii) tanθ = a0/ g
Thus, the string makes an angle tan-1 (a0/g) with the vertical.
Example 7: With what acceleration 'a’ should the box of figure descend so that the block of mass M exerts a force Mg/4 on the floor of the box?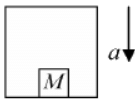
The block is at rest with respect to the box which is accelerated with respect to the ground. If observer is attached to box he will attached to accelerated frame which is moving in down ward direction .the observer will measure the Pseudo force in upward direction with magnitude Ma
(a) Mg downward (by the earth) and
(b) N upward (by the floor).
(c) Ma Pseudo force in upward direction
The equation of motion of the block is, therefore Mg - N - Ma = 0If N = Mg/4, the above equation gives a = 3g/4.
The block and hence the box should descend with an acceleration 3g/4.
Equation of Constraint
Limit to motion is known as constraint motion. The relationship between variable which actually equation of constraint is used to find independent variable which will describe independent motion of the system. Constraint equations are independent of applied force. It is very important tool to find relationship between accelerations of different particles, which can be better understand by following examples:
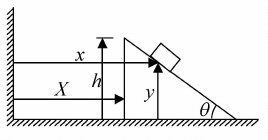
Example 8: A block moves on the wedge which in turns moves on a horizontal table, as shown in sketch, if the wedge angle is θ. H ow the acceleration of wedge and block are related?
Let the X be the horizontal coordinate of the end of the wedge and x a n d y be the horizontal and vertical coordinate h - y of the block as shown in figure.
Let h is height of the wedge. So from geometry (x - X) = (h - y) cot θ differentiation with respect to t is
Example 9: Two masses are connected by a string, which passes over a pulley accelerating upw ard at rate a , as shown in figure. If acceleration of the body 1 is a1 and body 2 is a2, what is relation between a, a1 and a2?
We know that length of string is fixed so from the figure,
l = πR + (yp - y1) + (yp - y2)
Differentiate with respect to I , 0 =,
Example 10: The pulley system shown in the figure. How the acceleration of the rope is related to the acceleration of the block?
Let us assume acceleration of the block is a and acceleration of end of rope is ar. Again the length of rope is fixed let say I
From the figure, l = X + πR + (X - h) + πR + (x - h)
where R is radius of pulley .differentiating with respect to
|
61 videos|23 docs|25 tests
|
FAQs on Newton’s Laws of Motion & Free Body Diagram - Mechanics & General Properties of Matter - Physics
| 1. What are Newton's Laws of Motion? |  |
| 2. How are Newton's Laws of Motion applied in real-life situations? |  |
| 3. What is a Free Body Diagram (FBD)? |  |
| 4. How do you construct a Free Body Diagram? |  |
| 5. Why are Free Body Diagrams important in the study of Newton's Laws of Motion? |  |