Newton's Second Law of Motion and Concept of Linear Momentum and Impulse | Science Class 9 PDF Download
Newton's Second Law of Motion
According to this law, the change in momentum of a body per unit time (i.e. rate of change of momentum) is directly proportional to the unbalanced force acting on the body and the change in momentum takes place in the direction of the unbalanced force on the body.
i.e. F ∝ dp/dt
where, dp = change in momentum and dt = time taken for this change in momentum.
Derivation of the Second Law of Motion
Consider a body of mass m moving with initial velocity u. Let a force F acts on the body for time t.
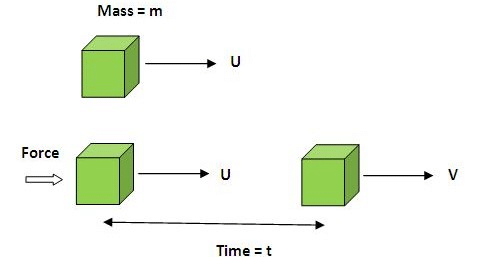 Initial momentum of the body, Pi = mu
Initial momentum of the body, Pi = mu
Final momentum of the body, Pf = mv
Now, change in momentum of the body = Pf - Pi = mv - mu = m(v - u)
Time taken to change this momentum = (t - 0) = t
∴ Rate of change of momentum =
According to the definition of Newton's second law of motion
Force applied µ rate of change of momentum
or ... (i)
Since v = u + at
Therefore, equation (i) can be written as
∴ F = ∝ ma
or F = k ma ... (ii)
where k is constant of proportionality,
If F = 1 unit
m = 1 unit
and a = 1 unit
Then from equation (ii) 1 = k or k = 1
Put this value of k = 1 in equation (ii), we get
F = ma
Thus, force acting on the body is directly proportional to (i) it's mass (m) and (ii) its acceleration (a). Equation (i) gives the mathematical form of Newton's second law of motion
Newton's Second Law of Motion in Vector Form
We know, force () and acceleration (
) are vector quantities, whereas mass (m) is a scalar quantity. Therefore, Newton's second law of motion can be written in vector form as
This relation shows that the direction of force applied to the body is same as that of the acceleration produced in the body.
Newton's First Law of Motion is a Special Case of Newton's Second Law of Motion
We know,
(Newton's Second law of motion)
If velocity of a body is constant i.e. u = u, then F = m × 0 = 0
Thus, no force is required to move a body with constant velocity or uniform velocity. If u = 0, then u is also zero, it means the body will remain at rest if no external force is applied on the body. This is the first law of motion.
Units of Force
We know, F = ma
If m = 1 unit and a = 1 unit
Then F = 1 unit
Thus, force is said to be unit force if it products unit acceleration in a body of unit mass.
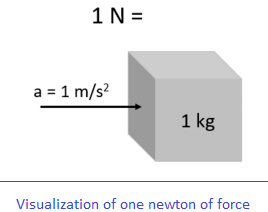
SI unit of force:
We know, F = ma
SI unit of mass,m = 1 kg
SI unit of acceleration, a = 1 ms-2
∴ SI unit of force = 1 kg × 1 ms-2 = 1 kg ms-2.
1 kg ms-2 is known as 1 newton (N).
∴ 1 newton (N) = 1 kg ms2
Definition of Newton (N): The force is said to be 1 newton if it products 1 ms2 acceleration in a body of 1 kg mass.
 C.G.S. unit of force:
C.G.S. unit of force:
We know, F = ma
In CGS system, unit of mass, m = 1 g
unit of acceleration, a = 1 cm s-2
∴ 1 unit of force = 1 g × 1 cm s2 = 1 g cm s-2
1 g cm s-2 is known as 1 dyne
1 dyne = 1 g cm s-2
Definition of dyne: The force is said to be 1 dyne if it produces 1 cm s-2 acceleration in a body of 1 g mass.
Relation between newton and dyne
We know, 1 newton (N) = 1 kg ms2 ... (i)
Now 1 kg = 1000 g = 103 g
1 m = 100 cm = 102 cm
Put these values in equation (i), we get
∴ 1 newton = 103 g × 102 cm s-2 = 105 g cm s-2
But 1 g cm s- 2 = 1 dyne
∴ 1 newton = 105 dyne
Newton's Second Law in Terms of Linear Momentum
Definition: The rate of change of momentum of a body with respect to time is directly proportional to the external force acting on the body and takes place in the direction of the force.
Suppose a body of mass m is acted upon by an unbalanced external force F which creates an acceleration a in the body. Let the initial velocity of the body be u. Let the force continues to act for a time interval t and the final velocity of the body be v. Then we can write
Here, mv = Final momentum of the body (Pf )
mu = Initial momentum of the body (Pi )
Then mv - mu = (Pf - Pi ) represents the change in momentum.
The change in momentum written as Δp and is called delta P.
Some Applications of
Example 1. A cricket player lowers his hands while catching a ball.
By doing so the player increases t, the time interval for the change in momentum. Because of this the force experienced by his hands is less.
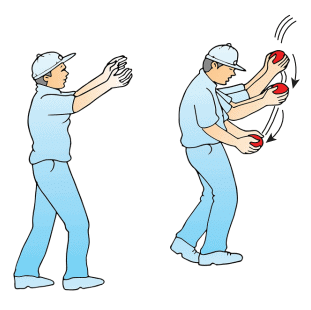 A fielder pulls his hands gradually with the moving ball while catching it.Example 2. A karate player breaks the pile of the tiles or bricks with a single blow.
A fielder pulls his hands gradually with the moving ball while catching it.Example 2. A karate player breaks the pile of the tiles or bricks with a single blow.
Example 3. Our hand hurts more when we hit the wall than when we hit a sponge seat of a car.
Solved Problems
Ex. When a force of 40 N is applied on a body it moves with an acceleration of 5 ms-2. Calculate the mass of the body.
Sol. Let m be the mass of the body.
Given : F = 40 N, a = 5 ms-2
From the relation F = m a we have 40 = m × 5
or m = 40/5 = 8 kg
Ex. It is required to increase the velocity of a scooter of mass 80 kg from 5 to 25 ms-1 in 2 seconds. Calculate the force required.
Sol. Given : m = 80 kg, u = 5 ms-1 v = 25 ms-1 and t = 2s
Now acceleration
Force = mass × acceleration of F = ma
Therefore, F = 80 × 10 = 800 N
Ex. Two blocks made of different metals identical in shape and sizes are acted upon by equal forces which cause them to slide on a horizontal surface. The acceleration of the second block is found to be 5 times that of the first. What is the ratio of the mass of the second to the first?
Sol. Let, mass of the first block = m1
Acceleration of the first block = a1
Mass of the second block = m2
Acceleration of the second block = a2
Also, a2 = 5 a1
If the force acting on each block be F. Then, F = m1 a1 and F = m2 a2 = m2 × 5 a1
or m1a1 = m2a2 = m2 × 5a1
or m1 = 5m2
This gives, .Thus, the mass of the second block is one-fifth that of the first block.
Ex. An object undergoes an acceleration of 8 ms-2 starting from rest. Find the distance travelled in 1 second.
Sol. We are given,
Acceleration, a = 8 ms-2
Initial velocity, u = 0
Time interval, t = 1 s
Distance travelled, S = ?
Using the equation of motion, , one gets
The object travels a distance of 4m.
Higher Order Thinking Skills
Impulse
The forces which act on bodies for short time are called impulsive forces. For example:
(i) In hitting a ball with a bat,
(ii) in driving a nail into a wooden block by a hammer,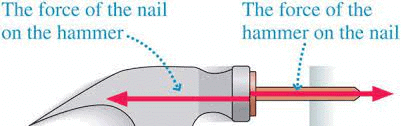 (iii) in firing a gun, etc.
(iii) in firing a gun, etc.
An impulsive force does not remain constant but changes first from zero to maximum and then from maximum to zero. Thus it is not possible to measure easily the value of impulsive force because it changes with time. In such cases, we measure the total effect of the force, called impulse.
Hence impulse of a force is a measure of total effect of the force. It is given by the product of average force and the time for which the force acts on the body; i.e.,
Impulse = Change in linear momentum
Impulse is a vector quantity
SI unit of impulse is N-s and kg ms-1
CGS unit = dyne-sec and g cm s-1.
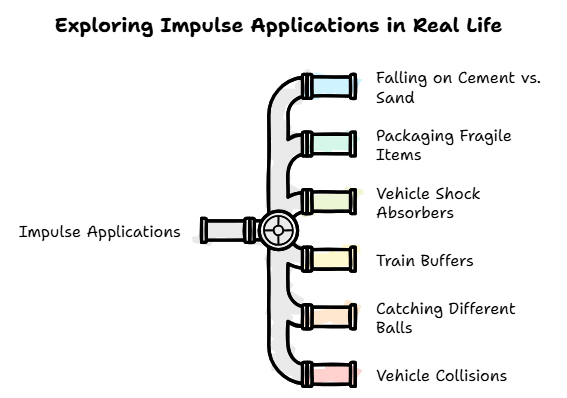
Applications of the Concept of Impulse
1. When a person falls from a certain height on a cemented floor, the floor does not yield. The total change in linear momentum is produced in a smaller interval of time. Therefore, as explained above, the floor exerts a much larger force. Due to it, a person receives more injury.
2. On the other hand, when a person falls on a heap of sand, the sand yields. The same change in linear momentum is produced in much longer time. The average force exerted on the person by the heap of sand is, therefore, much smaller and hence the person is not hurt.
3. China wares and glasswares are wrapped in paper or straw pieces before packing. In the event of fall, impact will take a longer time to reach the glass/chinawares through paper/straw. As a result, the average force exerted on the china or glassware is small and chances of their breaking reduce.
4. The vehicles like scooter, car, bus, truck etc. are provided with shockers. When they move over an uneven road, impulsive forces are exerted by the road. The function of shockers is to increase the time of impulse. This would reduce the force/jerk experienced by the rider of the vehicle.
5. Bogies of a train are provided with the buffers. They avoid severe jerks during shunting of the train.
Due to the presence of buffers, time of impact increases. Therefore, force during jerks decreases. Hence the chances of damage decreases.
6. It is difficult to catch a cricket ball than to catch a tennis ball. The cricket ball is heavier has much larger momentum and therefore, exerts a much larger force on the hands during catch, in comparison to the force exerted by tennis ball.
7. In a head on collision between two vehicles, change in linear momentum is equal to sum of the linear momentum of the two vehicles. As time of impact is small, an extremely large force developed which causes damage to both vehicles.
8. An athlete is advised to come to stop slowly, after finishing a fast race, so that time of stop increases and hence force experienced by him decreases.
|
84 videos|478 docs|59 tests
|
FAQs on Newton's Second Law of Motion and Concept of Linear Momentum and Impulse - Science Class 9
| 1. What is Newton's Second Law of Motion and how is it mathematically expressed? |  |
| 2. How do linear momentum and impulse relate to Newton's Second Law? |  |
| 3. Can you provide a real-life example demonstrating Newton's Second Law of Motion? |  |
| 4. What is the significance of the concept of impulse in sports? |  |
| 5. How does the conservation of momentum relate to collisions and Newton's Second Law? |  |






















