Newton's Third Law of Motion | Science Class 9 PDF Download
| Table of contents |

|
| Newton's Third Law of Motion |

|

|
|
| Important Points to Remember |

|
| Competitive Window |

|
Newton's Third Law of Motion
Definition
For each and every action, there is equal and opposite reaction.
lf a body A exerts force on another body B, then B exerts a force -
on A, the two forces acting along the same line. The two forces
and -
connected by Newton's third law are called action-reaction pair. Any one may be called 'action' and the other 'reaction'.
Action and reaction acts on different bodies hence they never cancel each other.
Note: Action and reactions forces occur simultaneously. It is wrong to think that first action occurs and it is followed by reaction.
An important conclusion: When action-reaction forces are acting on two bodies of masses mA and mB then
From eqn. FAB = -BA
mAaA = -mBaB
Misconception: The action and reaction forces acting on a body are equal and opposite and therefore cancel out the effect of each other.
Actual Concept: Action and reaction do not cancel out the effect of each other because they act on different bodies.
Misconception: Any pair of equal and opposite forces are an action-reaction pair.
Actual Concept: Only those forces from an action-reaction pair that involve the two bodies responsible for action-reaction.
Some Other Examples of Newton's Third Law
1. When a bullet is fired from a gun, we observe recoiling of the gun. The gun acts on bullet i.e., exerts a force on the bullet; simultaneously, the bullet reacts on the gun.
2. While walking or running, you push the ground in the backward direction with your feet. The ground simultaneously exerts a force of equal magnified in the forward direction on feet. This force enables us to walk.
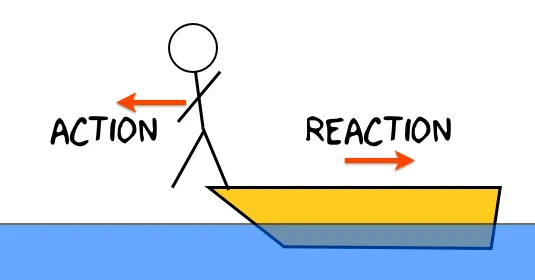
3. When a man jumps from a boat, the boat also experiences a backward jerk. This is due to the action-reaction pair as shown in figure.
4. Inflate a balloon and leave it. You will observe that the balloon moves in opposite direction to the opening in balloon through which the air is coming out.
5. A ball rebounds after striking against a floor.
When a ball strikes against a floor, it exerts a force on the floor. According to Newton's third law of motion, the floor exerts an equal and opposite force on the ball. Due to this reaction, the ball rebounds.
6. How do we swim ?
While swimming, a swimmer pushes the water backward with his hands. The reaction offered by the water to the swimmer pushes him forward.
7. A boatman pushes the river bank with a bamboo pole to take his boat into the river.
When the boatman pushes the river bank with a bamboo pole, the river bank offers an equal and opposite reaction. This reaction helps the boat to move into the river.
8. Why a fireman struggles to hold a hose-pipe ?
A fireman has to make a great effort to hold a hose-pipe to throw a stream of water on fire to extinguish it. This is because the stream of water rushing through the hose-pipe in the forward direction with a large speed exerts a large force on the hose-pipe in the backward direction.
 |
Download the notes
Newton's Third Law of Motion
|
Download as PDF |
Important Points to Remember
- Unit of force is dyn or newton whereas that of mass is gram or kilogram.
- It is wrong to say "Weight of Ankit is 40 kg." We should say "Mass of Ankit is 40 kg" or "Weight of Ankit is 40 × 9.8 = 392N."
- 1 metric ton = 1,000 kg , 1 quintal = 100 kg
- 1 metric ton = 10 quintals , 1 kg = 1,000 g
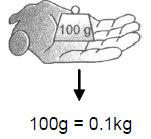
Competitive Window1. In solving the numericals, always take the force in absolute units i.e., in dynes or newtons. 2. 1 N = 105 dyn. 3. The kg f (kilogram force) and kg wt (kilogram weight) are two names of same quantity i.e., of practical units of force. 4. Momentum is a vector quantity. 5. Weight of the body or force applied should be never states in kg. Kilogram is a unit of mass and not of weight or force. Never say, "My weight is 50 kg". Say "My weight is 50 kg for 50 kg wt or 50 × 9.8 N" or say, "My mass is 50 kg". 6. Hold 0.1 kg on your hand placed parallel to earth. Your hand is applying a force of nearly 1 N (0.98 N to be exact). 7. In all numericals, use only absolute units (N or dyn). If the force is given in kg f or g f, convert these to N or dyn. |
|
84 videos|384 docs|61 tests
|
FAQs on Newton's Third Law of Motion - Science Class 9
| 1. What is Newton's Third Law of Motion? |  |
| 2. How does Newton's Third Law of Motion relate to the Law of Conservation of Momentum? |  |
| 3. Can you provide an example of Newton's Third Law of Motion? |  |
| 4. How does Newton's Third Law of Motion apply to everyday life? |  |
| 5. Can you explain the concept of a competitive window in the context of Newton's Third Law of Motion? |  |