Nodal Voltage Analysis | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download

Introduction

• Nodal Voltage Analysis complements the previous mesh analysis in that it is equally powerful and based on the same concepts of matrix analysis. As its name implies, Nodal Voltage Analysis uses the “Nodal” equations of Kirchhoff’s first law to find the voltage potentials around the circuit.
• So by adding together all these nodal voltages the net result will be equal to zero. Then, if there are “n” nodes in the circuit there will be “n-1” independent nodal equations and these alone are sufficient to describe and hence solve the circuit.
• At each node point write down Kirchhoff’s first law equation, that is: “the currents entering a node are exactly equal in value to the currents leaving the node” then express each current in terms of the voltage across the branch. For “n” nodes, one node will be used as the reference node and all the other voltages will be referenced or measured with respect to this common node.

Nodal Voltage Analysis Circuit

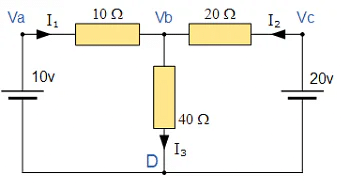
• In the above circuit, node D is chosen as the reference node and the other three nodes are assumed to have voltages, Va, Vb and Vc with respect to node D. For example;
  
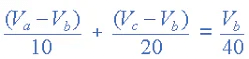
• As Va = 10v and Vc = 20v , Vb can be easily found by:
  
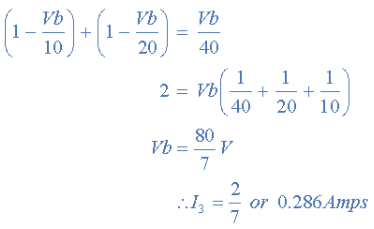
• again is the same value of 0.286 amps, we found using Kirchhoff’s Circuit Law in the previous tutorial.
• From both Mesh and Nodal Analysis methods we have looked at so far, this is the simplest method of solving this particular circuit. Generally, nodal voltage analysis is more appropriate when there are a larger number of current sources around. The network is then defined as: [I] = [Y] [V] where [I] are the driving current sources, [V] are the nodal voltages to be found and [Y] is the admittance matrix of the network which operates on [V] to give [I].

Summary

The basic procedure for solving Nodal Analysis equations is as follows:

• Write down the current vectors, assuming currents into a node are positive. ie, a (N x 1)  matrices for “N” independent nodes.
• Write the admittance matrix [Y] of the network where:
  Y₁₁ = the total admittance of the first node.
  Y₂₂ = the total admittance of the second node.
  R_JK = the total admittance joining node J to node K.
• For a network with “N” independent nodes, [Y] will be an (N x N) matrix and that Ynn will be positive and Yjk will be negative or zero value.
• The voltage vector will be (N x L) and will list the “N” voltages to be found.