Non Linear Functions Problems | Mathematics for Digital SAT PDF Download
| Table of contents |

|
| What is a function? |

|
| How do I evaluate functions? |

|
| How do I evaluate composite functions? |

|
| How do I compose functions? |

|
What is a function?
A function takes an input and produces an output. In function notation, f(x), f is the name of the function, a is the input variable, and f(x) is the output.
For example, given f(x) = 2x + 1, the expression 2x + 1 works as instructions on what to do with the input x. In this case, the input x is multiplied by 2, then 1 is added to the product.
How do I evaluate functions?
Evaluating functions algebraically and using tables
When we encounter an algebraic function, we can find the value of the function at specific inputs. For example, for f(x) = 2x + 1, we can calculate f(2), the output of the function f when its input, x, is equal to 2.
What are the steps?
To evaluate a function at a specific input value:
- Plug in the input value for the input variable wherever it appears.
- Perform the operations specified by the function to calculate the ouput.
Example: If f(x) = x3- 9, what is the value of f(-2)?
Sol: We need to plug-2 into f for x to evaluate f(-2):
f(x) = x3 -9
f(-2) = (-2)3-9
=-8-9
= -17
-17 is the value of f(-2).
With algebraic functions, we can evaluate the function using multiple inputs to create multiple input-output pairs. These input-output pairs can be put in a table, as shown below for f(x) = 2x + 1.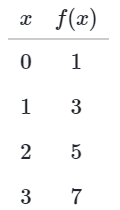 Sometimes, a table of input-output pairs is provided without an algebraic function. Consider the table below.
Sometimes, a table of input-output pairs is provided without an algebraic function. Consider the table below.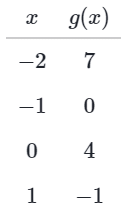 The table contains four input-output pairs. We can interpret the information in the table as:
The table contains four input-output pairs. We can interpret the information in the table as:
- g(-2) = 7
- g(-1) = 0
- g(0) = 4
- g(1) = -1
To evaluate a function using a table:
- Find the input value you're looking for in the input column (typically the left column with a header of the input variable such as x).
- Find the corresponding output value in the output column.
Example: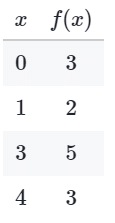 Based on the table above, what is the value of f (3)?
Based on the table above, what is the value of f (3)?
Sol: In the table, the inputs are in the x column, and the outputs are in the f(x) column.
The value of f(3) is in the same row as the x-value of 3, so f(3) = 5.
5 is the value of f(3).
How do I evaluate composite functions?
Evaluating composite functions algebraically and using tables
A composite function uses the output of one function as the input of another. For example, for f(g(x)):
- x is the input to function g.
- g(x) is the input to function f.
As such, composite functions should be worked from the inside out. Order matters when evaluating composite functions: g(f(x)) is not the same as f(g(x))!
For example, for f(x) = x2 and g(x) = x + 1, f(g(1)) = 4, but g(f(1)) = 2.
To evaluate composite functions at a specific input value:
- Plug in the input value for the input variable wherever it appears in the inner function.
- Perform the operations specified by the inner function to calculate the output. This output becomes the input of the outer function.
- Plug in the result of Step 2 for the input variable wherever it appears in the outer function.
- Perform the operations specified by the outer function to calculate the final output.
Example: If f(x) = 2x + 1 and g(x) = x2 -2x+1, what is the value of f(g(-1))?
Sol: We need to input -1 into g, then use the output as the input for f.
First, let's evaluate g(-1):
g(x) = x2-2x+1
g(-1)=(-1)2-2(-1)+1
=1+2+1
= 4
Next, we need to input 4 into f to evaluate f(4):
f(x) = 2x + 1
f(4) = 2(4) +1
= 8+1
= 9
9 is the value of f(g(-1)).
Composite functions can also be evaluated using a table. The table can have an additional column for a total of three: one column for input and two columns for the outputs of two functions. Consider the table for f(x) = x2 and g(x) = x + 1:
From the table, we can tell that g(1) = 2, and f(2) = 4. Therefore, f(g(1)) = 4.
To evaluate composite functions at a specific input value given a table:
- Find the output value for the inner function corresponding to the specific input value. This is also the input value of the outer function.
- Find the output value for the outer function corresponding to the input of the result of Step 1.
Example:
The table above provides the values of functions f and g at several values of x. What is the value of g(f(2))?
Sol: We need to identify the value of f for x = 2, then use that value as the value of x to identify the value of g.
According to the table, when x = 2, f(x) = 5. When x = 5, g(x) = 16:
g(f(2)) = g(5) = 16
16 is the value of g(f(2)).
How do I compose functions?
Inputting expressions instead of values into functions
In addition to inputting a specific value, we can also input one function into another function, which creates a composite function defined by a single expression.
For example, for f(x) = x2 and g(x) = x + 1, f(g(x)) replaces each instance of x in f with g(x), which is equal to x + 1: f(g(x)) = (x + 1)2. Inputting an expression into a function, e.g., f(x + 1), works similarly.
A function can also be defined in terms of another function. For example, for f(x) = x2 and g(x) = f(x) + 1, we can replace the f(x) in function g with 22: g(x) = x2 + 1.
If you find yourself struggling to rewrite complex functions, you might want to brush up on the Operations with polynomials and Operations with rational expressions skills, which have their own lessons.
To compose two functions:
- Plug in the expression that defines the inner function wherever the input variable appears in the outer function.
- Perform the operations specified by the outer function. Combine like terms as needed.
|
204 videos|126 docs|75 tests
|
FAQs on Non Linear Functions Problems - Mathematics for Digital SAT
| 1. How can I identify a non-linear function? |  |
| 2. How do I solve problems involving non-linear functions on the SAT exam? |  |
| 3. Can non-linear functions be represented algebraically? |  |
| 4. How do I determine the domain and range of a non-linear function? |  |
| 5. How can I use composite functions to solve non-linear function problems on the SAT? |  |















