Notes: Fractions | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
Fractions represent parts of a whole and are essential for mastering mathematical operations. They are a key topic in CTET, TET, and other educational exams. This document covers the basics of fractions, including their types, operations helping aspirants develop a strong foundation for teaching and exam success.
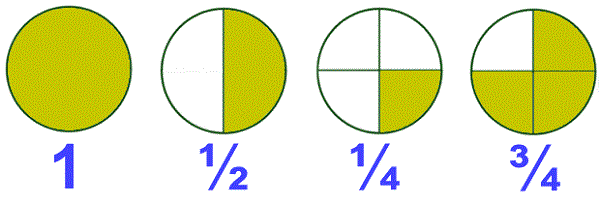
What is a Fraction?
A fraction is a part of a whole. A whole can be a group of objects or a single object.
Let us understand fractions with the help of an example:
Ethan is celebrating his birthday at home. His mother has baked a cake for his birthday. When his friends came home, he cut the cake.
His mother wants to distribute the cake equally among all his friends.
There are six people (including Ethan’s mother) at the party.
So, his mother cuts the cake into 6 equal parts.
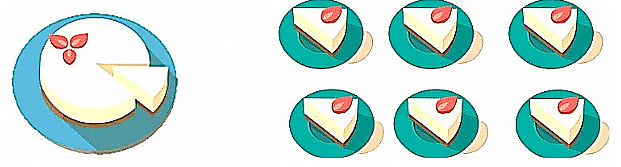 Fractions of a Cake
Fractions of a Cake
Can you tell what fraction of the cake Ethan gets?
Total number of slices of cake = 6
Ethan got (one-sixth) part of the cake.
So, Ethan ate one part out of six parts of the cake.
Ethan and his friends had learnt about fractions at school.
So, one of Ethan’s friends, while eating the cake, cuts his slice of cake into two equal pieces and asks Ethan what fraction of the whole slice was that piece?
So Ethan said that each equal piece is one-half of one whole slice, and the two pieces together will be one whole slice.
Example: Write the fraction representing the shaded portion.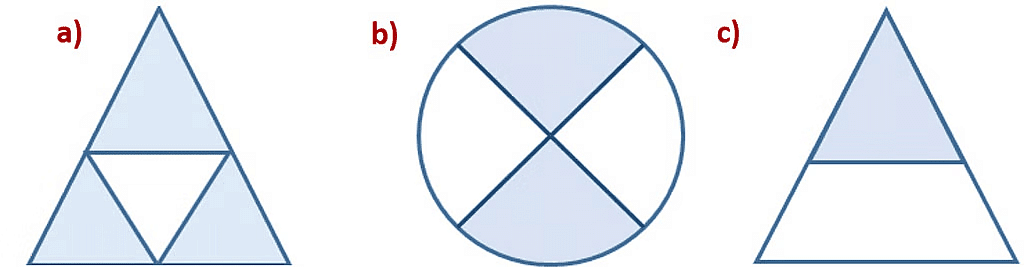 a) The given figure is divided into 4 equal parts.
a) The given figure is divided into 4 equal parts.
Number of shaded parts = 3
Total number of equal parts = 4
Fraction representing the shaded portion = 3/4
b) The given figure is divided into 4 equal parts.
Number of shaded parts = 1
Total number of equal parts = 4
Fraction representing the shaded portion = 2/4 or 1/2

c) The given figure is not divided into equal parts. For making fractions the figure should be divided into equal parts.
Fractions on a Number Line
Whole numbers are represented on the number line as shown here:
A fraction can also be represented on the number line.
Examples:
- Consider a fraction 1/2.
1/2 is greater than 0, but less than 1.
Divide the space between 0 and 1 into two equal parts. We can show one part as the fraction 1/2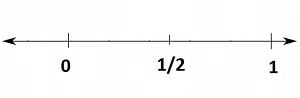
- Consider another 1/5.
1/5 fraction is greater than 0, but less than 1.
Divide the space between 0 and 1 into five equal parts. We can show the first part as 1/5 the second as 2/5 the third as 3/5 the fourth as 4/5 and the fifth part as 5/5=1.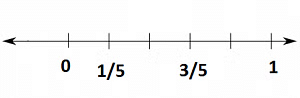
Types of Fractions
Let us understand the different types of fractions. There are three types of fractions. They are:
1. Proper fractions
2. Improper fractions
3. Mixed fractions
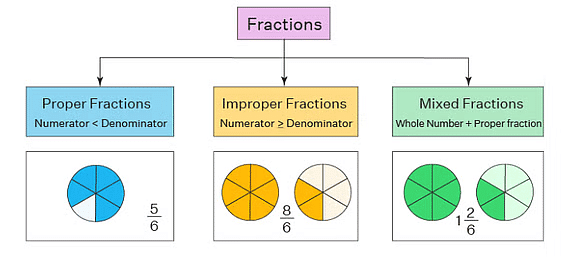 Types of Fractions
Types of Fractions
Proper Fractions
A proper fraction is a number representing a part of a whole.
- In a proper fraction, the number in the denominator shows the number of parts into which the whole is divided, while the number in the numerator shows the number of parts that have been taken.
- Here, the numerator is always less than denominator such fractions are termed as a proper fraction.
- Examples of Proper Fractions:

Question: Give the proper fraction:
Whose denominator is 9 and numerator is 5.
Given numerator is 5 and denominator is 9
We know that Fraction = Part/ Whole
So, Fraction = 5/9
Hence, required fraction is 5/9
Improper and Mixed Fractions
Improper Fractions
- A fraction in which the numerator is bigger than the denominator is called an improper fraction.
- Examples of Improper Fractions:
Mixed Fractions
- A combination of a whole and a part is said to be a mixed fraction.
- Examples of Mixed Fractions:
 Summary of Proper, Improper and Mixed Fraction
Summary of Proper, Improper and Mixed Fraction
Conversion of Improper fraction into Mixed fraction and Vice Versa
1. Conversion of improper fraction into mixed fraction
An improper fraction can be expressed as mixed fraction by dividing the numerator by the denominator of the improper fraction to obtain the quotient and the remainder. Then the mixed fraction will be.
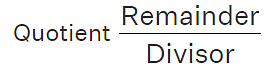
Example: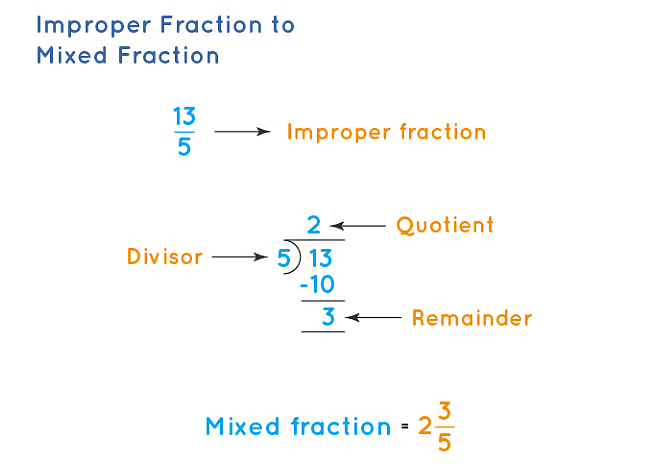 Improper fraction to Mixed Fraction 2. Conversion of mixed fraction into improper fraction:
Improper fraction to Mixed Fraction 2. Conversion of mixed fraction into improper fraction:
A mixed fraction can also be converted to an improper fraction. Let us understand this by taking an example of a mixed fraction 2 x 4/5. Here 2 is the whole number, 4 is the numerator and 5 is the denominator.
Let us convert this mixed fraction to an improper fraction using the following steps and the explanation given below.
- Step 1: Multiply the denominator of the mixed fraction with the whole number part. In this case, 5 × 2 = 10
- Step 2: Add the numerator to the product obtained from Step 1. Here, 4 + 10 = 14.
- Step 3: Write the improper fraction with the sum obtained from Step 2 in the numerator/denominator form. Here, it will be 14/5.
 Mixed Fraction to Improper Fraction
Mixed Fraction to Improper Fraction
Equivalent Fractions
These are fractions that represent the same value or part of a whole, even though they have different numerators and denominators.
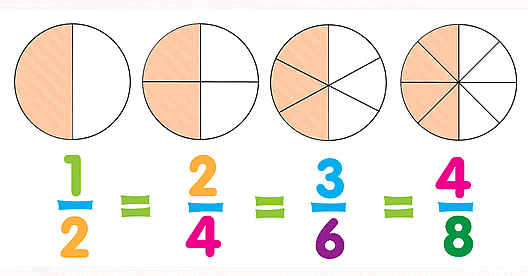 Equivalent Fractions
Equivalent Fractions
How to Find Equivalent Fractions
Multiplying Both Numerator and Denominator: To find an equivalent fraction, multiply both the numerator (top number) and the denominator (bottom number) by the same number.
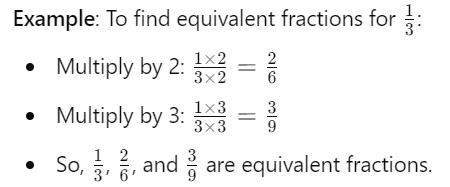
Dividing Both Numerator and Denominator: Alternatively, you can divide both the numerator and the denominator by the same number to find equivalent fractions.
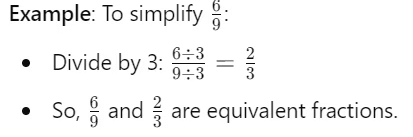
Equivalent fractions represent the same part of a whole because they are different ways of expressing the same proportion. When you multiply or divide the numerator and denominator by the same number, you are essentially scaling the fraction but keeping the same overall value.
Example 1: Find any 3 equivalent fractions of  .
.
Ans:
- If we multiply both the numerator and denominator with the same non zero number, we will get its equivalent fraction.If we multiply given fraction by:
 =
= 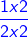 =
= 
 =
=  =
= 
 =
=  =
= 
Example 2: Are 1/3 and 4/7 equivalent?
Ans: No, because they do not represent the same part of a whole.
Simplest Form of Fraction
A fraction is said to be in its simplest form or its lowest form if its numerator and denominator have no common factor except one.
 Simplest Form of FractionThe simplest form of a given fraction can also be found by dividing its numerator and denominator by its highest common factor (HCF).
Simplest Form of FractionThe simplest form of a given fraction can also be found by dividing its numerator and denominator by its highest common factor (HCF).
Here are some solved examples related to the above topic:
Example : Find the simplest form of the fraction 11/33
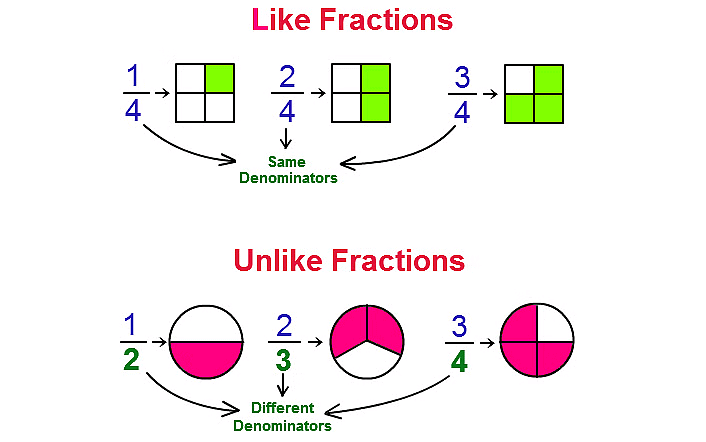
Like Fractions
Like fractions and unlike fractions refer to the relationships between the denominators of two or more fractions.
 Like and Unlike Fractions
Like and Unlike Fractions
1. Like Fractions
- Like fractions have the same denominator.
- Example: 3/4 and 2/4 are like fractions because they share the common denominator 4.
2. Unlike Fractions
- Unlike fractions have different denominators.
- Example: 2/5 and 3/8 are unlike fractions because they have different denominators (5 and 8).
Note: Understanding whether fractions are like or unlike is important when performing operations like addition, subtraction, multiplication, or division with fractions.
- For example, adding or subtracting like fractions is straightforward since you only need to operate on the numerators while keeping the common denominator.
- On the other hand, when dealing with unlike fractions, you typically find a common denominator before performing operations.
How do We Compare Fractions?
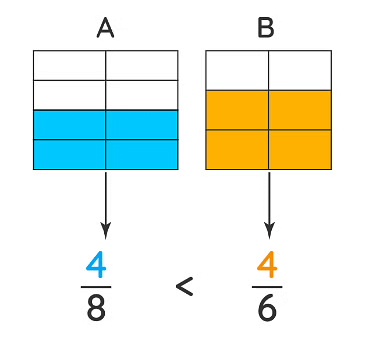 Comparing Fractions using Visualisation
Comparing Fractions using Visualisation
1. Comparing Like Fractions
In like fractions, the fraction with the greater numerator is greater.
 Comparing Like Fractions
Comparing Like Fractions
- Example: Among fractions 5/7 and 3/7, 5/7 is greater than 3/7 as 5 is greater than 3.
- Two fractions are unlike fractions if they have different denominators.
Example: Compare: 5/12 and 17/12.
- Step 1: First, observe the denominators of the given fractions, i.e., 5/12 and 17/12. Here, the denominators are the same for both fractions.
- Step 2: Now, compare the numerators of the given fractions. We can observe that 17 > 5.
- Step 3: We know that the fraction with the larger numerator is larger. Hence, 5/12 < 17/12.
2. Comparing Unlike Fractions
- If two fractions with the same numerator but different denominators are to be compared, then the fraction with the smaller denominator is the greater of the two.
- To compare fractions with unlike denominators, we have to convert them to like denominators for which we have to find the Least Common Multiple (LCM) of the denominators. As the denominators are made equal, we can compare the fractions with ease.
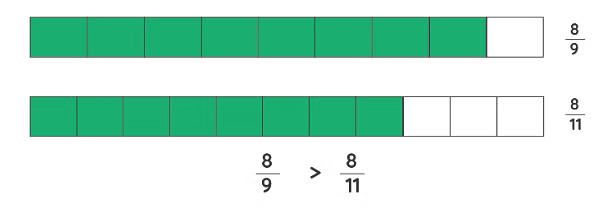 Comparing Unlike Fractions
Comparing Unlike Fractions
Example: Compare: 1/4 and 2/3.
Step 1: First, observe the denominators of the given fractions, i.e., 1/4 and 2/3. Since the denominators are different make them equal by finding the LCM of 4 and 3. LCM(4,3) = 12.
Step 2: Now, let us convert the given fraction in such a way that they have the same denominators. So, multiply the first fraction with 3/3, i.e., 1/4 × 3/3 = 4/12.
Step 3: Similarly, multiply the second fraction with 4/4, i.e., 2/3 × 4/4 = 8/12. Thus, the first fraction becomes 4/12 and the other becomes 8/12.
Step 4: Compare the obtained new fractions, i.e., 4/12 and 8/12. As the denominators are the same, we will compare the numerators. We can observe that 4 < 8.
Step 5: The fraction that has a large numerator is the larger fraction. So, 8/12 > 4/12. So, 1/4 > 2/3.
Addition and Subtraction of Fractions:
Addition and subtraction of fractions involve combining or taking away portions of quantities represented by the fractions. Here's a brief overview:
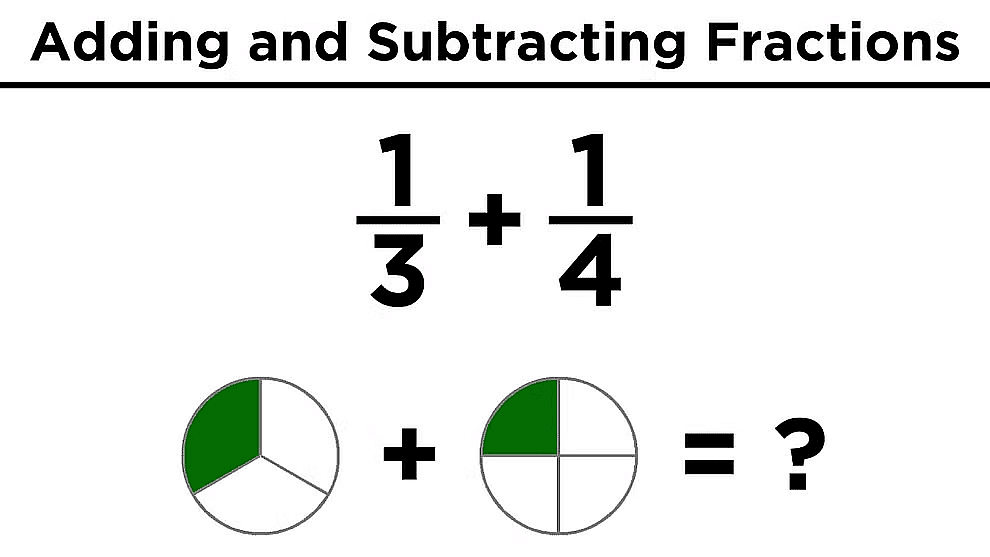
1. Addition and Subtraction of two like fractions
When we add or subtract like fractions, we add or subtract their numerators and the denominator remains the same.1)  +
+ 
The two fractions are like fractions, so we add their numerators and keep the denominator the same. +
+  =
= 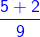 =
= 
2)  −
− 
Here, the given fractions are like fractions. So, we subtract their numerators and keep the denominator the same.
 −
−  =
= 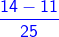 =
= 
2. Addition and Subtraction of two unlike fractions
When we add or subtract unlike fractions we follow the following steps:
1)  +
+ 
The given fractions are unlike fractions, so we first find LCM of their denominators.
LCM of 8 and 24 = 2 × 2 × 2 × 3 = 24
Now, we convert the fractions into like fractions.
(Changing the denominator of fractions to 24)
 =
=  and
and
 +
+  = =
= = 
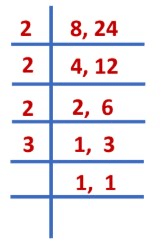
2)  -
- 
As the given fractions are unlike fractions, we find the LCM of their denominator.
LCM of 15 and 27 = 3 × 3 × 3 × 5 = 135
Next, we convert the fractions into like fractions
(Fractions with the same denominator)

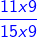 =
= 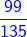 and
and 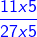 =
= 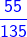
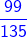 -
- 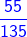 =
= 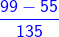 =
= 
3. Addition and Subtraction of Mixed Fractions
Note: Before applying any operations such as addition, subtraction, multiplication, etc., change the given mixed fractions to improper fractions.
After converting the mixed fractions to improper fractions, one can proceed with the calculations, which are as follows:
Adding Mixed Fractions
When it comes to adding Mixed or Improper fractions, we can have either the same denominators for both the fractions to be added or the denominators can differ too.
Here’s a step-wise method to add the improper fraction with same or different denominators.
 Adding improper fraction with same or different denominators
Adding improper fraction with same or different denominators
Subtracting Mixed Fractions
Here’s a step-wise explanation of how to Subtract the improper fraction with Same or Different Denominators.
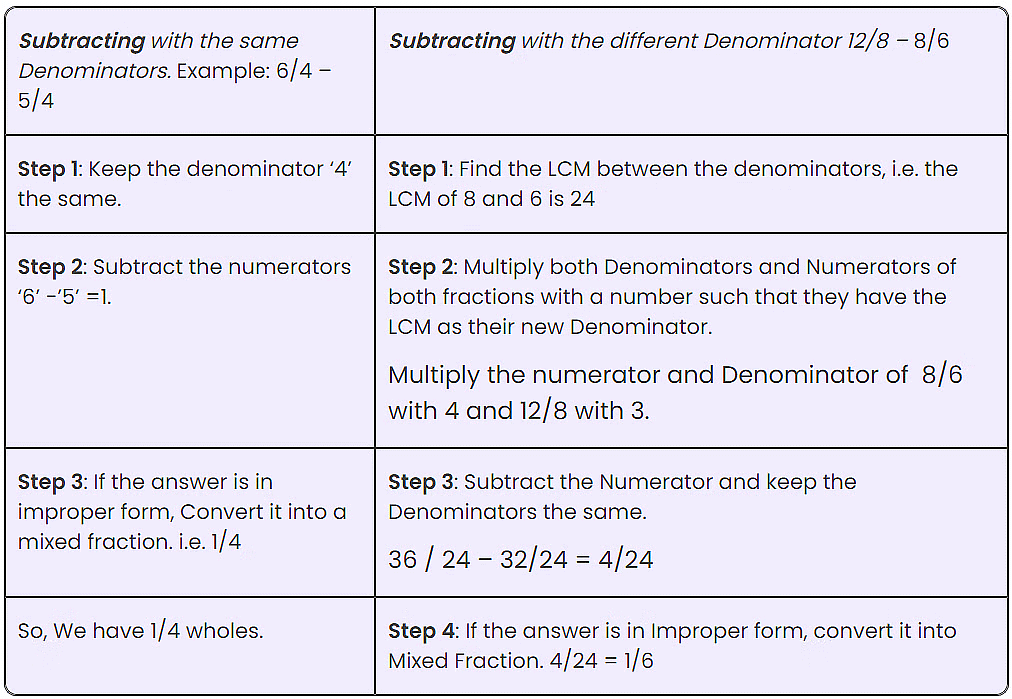
|
82 videos|300 docs|69 tests
|
FAQs on Notes: Fractions - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What is a fraction and how is it represented? |  |
| 2. How do you place fractions on a number line? |  |
| 3. What are proper, improper, and mixed fractions? |  |
| 4. How do you determine equivalent fractions? |  |
| 5. What are the steps for adding and subtracting fractions? |  |



















