Notes: Patterns | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Types of Patterns: |

|
| Pattern |

|
| Number Patterns |

|
| Border Patterns |

|
| Tiling Patterns |

|
Patterns are a fundamental concept in mathematics that is crucial for the CTET and other educational exams. Understanding patterns helps students recognize relationships, make predictions, and solve problems. Here's a brief overview:
A pattern is a sequence, series, or arrangement of elements that repeats or follows a predictable rule.
Patterns can be found in numbers, shapes, colors, movements, and processes.
Types of Patterns:
Number Patterns:
Arithmetic Sequence: A sequence where each term is obtained by adding a fixed number (common difference) to the previous term (e.g., 2, 4, 6, 8...).
Geometric Sequence: A sequence where each term is obtained by multiplying the previous term by a fixed number (common ratio) (e.g., 2, 6, 18, 54...).
Square Numbers: Patterns involving the squares of natural numbers (e.g., 1, 4, 9, 16...).
Triangular Numbers: Patterns involving the sums of consecutive natural numbers (e.g., 1, 3, 6, 10...).
Shape Patterns:
Repeating Shapes: Patterns formed by repeating a geometric shape (e.g., tessellations).
Symmetry Patterns: Patterns that exhibit symmetry, such as reflection or rotation symmetry (e.g., snowflakes, kaleidoscope designs).
Color Patterns:
Color Sequences: Patterns in color arrangements, such as alternating colors or gradients.
Behavioral Patterns:
Movement Patterns: Patterns in the movement of objects or organisms, such as periodic movements or migrations.
Pattern
A pattern is formed by repeating a unit, which may be a set of numbers or shapes, according to a rule.
Number Patterns
1. Square Numbers
Patterns of squares using dots can be made in two different ways as.
I. Rita uses coloured dots to make patterns of squares as:

1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 12
The number of dots in each square names a square number and this is so-called because the dots are arranged in a square shape.
A square number is obtained by multiplying the number by itself.
Now, can you name the next two square numbers and draw the square patterns?

II. Abhinav makes the square patterns as:
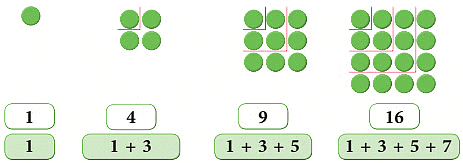
1 × 1 = 1
2 × 2 = 4 = 1 + 3
3 × 3 = 9 = 1 + 3 + 5
4 × 4 = 16 = 1 + 3 + 5 + 7
Thus, we observe that,
First square number = 1 = First odd number
Second square number = 4 = 1 + 3 = Sum of first two odd numbers
Third square number = 9 = 1 + 3 + 5 = Sum of first three odd numbers
Fourth square number = 16 = 1 + 3 + 5 + 7 = Sum of first four odd numbers
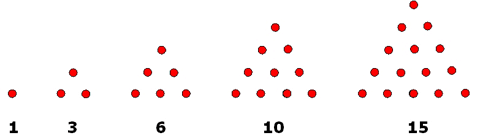
2. Triangular Numbers
Triangular patterns using dots can be made in two ways as given below.
The number of dots in each triangle is known as a triangular number.
1. Look at the pattern formed using dots.
The numbers 1, 3, 6, 10, ... show a triangular-shaped picture of dots. So, they are called triangular numbers.
Following the above pattern draw the next two triangular numbers using dots.

2. Look at the following triangular pattern by using dots.
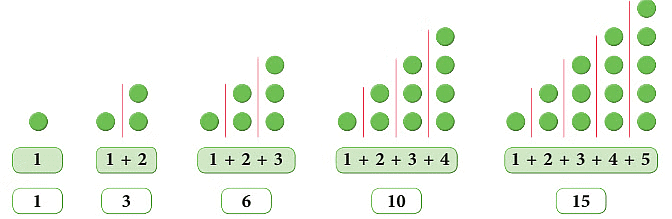
Thus, we observe the pattern as:
First triangular number = 1 = First natural number.
Second triangular number = 3 = 1 + 2 = Sum of first two natural numbers.
Third triangular number = 6 = 1 + 2 + 3 = Sum of first three natural numbers and so on.
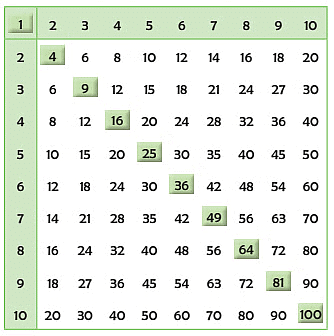
Now, see what happens if you add two consecutive triangular numbers?
1 + 3 = 4
3 + 6 = 9
6 + 10 = 16
10 + 15 = 25
Square numbers
Edurev Tips: We get a square number on adding two
We get a square number by adding two consecutive triangular numbers. The square numbers are shown in a multiplication square as given alongside. They lie on a diagonal line.
Border Patterns
Observe the following patterns around you. Patterns in the border of dupatta, bedsheets,
floors, etc.

These are called border patterns. We see that border patterns enhance the original beauty.
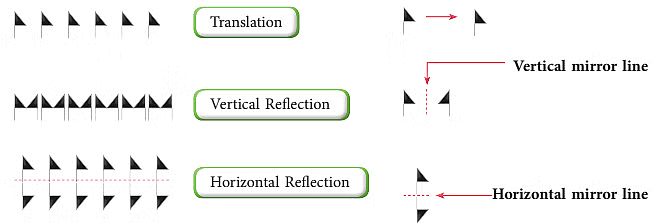
These border patterns are formed by repeating a certain shape or unit in one direction.
Following a basic symmetry repetition, maybe of translation, vertical reflection or horizontal reflection.
To understand better, let us take an example.
Consider the symbol  as the basic unit or shape in the border pattern. We can get the
as the basic unit or shape in the border pattern. We can get the
following patterns when  follows the different symmetries as shown below.
follows the different symmetries as shown below.
Tiling Patterns
The most familiar examples of translations are the patterns formed by pairing stones or
bricks and the cross-section of beehives.
A tiling pattern is formed by the repetition of a single unit or shape which when repeated, fills the plane with no gaps and no overlaps.
Look at the following patterns.
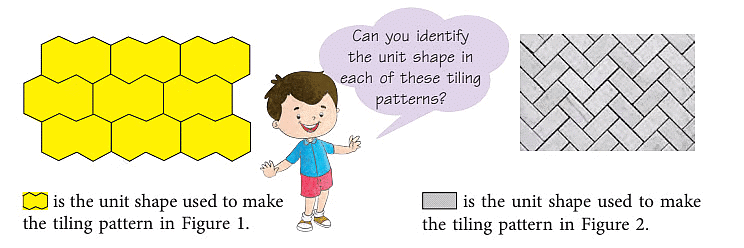
Now, observe these patterns. Are they tiling patterns? If not, then why not?

Thus, the above patterns are not tiling patterns.
Tiling Patterns Around Us
Tiling patterns are found in things around us.

Multiple tiling patterns can be made using a single shape as shown.

|
30 videos|210 docs|69 tests
|




















