Notes: Solids Around Us | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Solids |

|
| Pyramid |

|
| Nets |

|
| Viewing 3d Shapes |

|
| Reflection and Symmetry |

|
| Section |

|
| Planes of Symmetry |

|
| Rotational Symmetry |

|
| No Rotational Symmetry |

|
Solids are an integral part of our daily lives, forming the basic structure of the world around us. Understanding the properties and types of solids is a fundamental aspect of early education, especially in the context of the Central Teacher Eligibility Test (CTET).
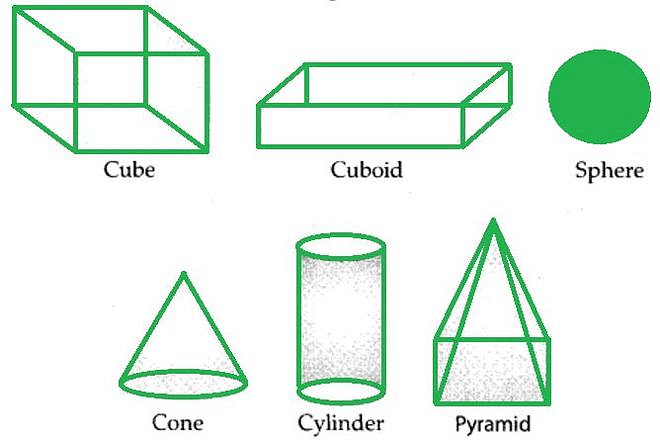
Types of Solids:
Solids can be classified into various categories based on their shapes and structures. Common types include:
Cubes and Cuboids: Examples include dice, boxes, and bricks. These shapes have six flat faces, with cubes having equal edge lengths, while cuboids have different edge lengths.
Spheres: Examples include balls and globes. Spheres are perfectly round and have no edges or vertices.
Cylinders: Examples include cans and pipes. Cylinders have two circular faces and one curved surface.
Cones: Examples include ice cream cones and traffic cones. Cones have a circular base and a pointed top.
Pyramids: Examples include pyramids in Egypt and certain types of roofs. Pyramids have a polygonal base and triangular faces that meet at a point.
Solids
Look around you! Do you see any of the objects around you resembling the shapes shown here? A few objects are shown below:
A few objects are shown below: What special things do you notice about these shapes?
What special things do you notice about these shapes?
- You can hold them in your hands.
- They are solids.
You have also learnt about some basic shapes drawn below: You can touch them only on paper, you cannot hold them in your hands. These shapes are called 2D shapes or 2-dimensional shapes. They have two dimensions, length and breadth.
You can touch them only on paper, you cannot hold them in your hands. These shapes are called 2D shapes or 2-dimensional shapes. They have two dimensions, length and breadth.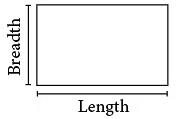 The shapes shown in the beginning of the chapter, also called solid shapes, are known as 3D shapes or 3-dimensional shapes. They have three dimensions: length, breadth and height.
The shapes shown in the beginning of the chapter, also called solid shapes, are known as 3D shapes or 3-dimensional shapes. They have three dimensions: length, breadth and height.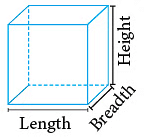
Faces, Edges and Vertices of a Solid Figure
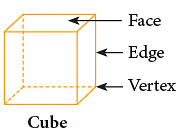
- A face is a flat surface.
- An edge is the line segment where two faces meet.
- A vertex is a point or corner where two or more edges meet.
As you can observe, the faces of a cube and cuboid are flat, whereas a cylinder, cone and sphere have curved faces.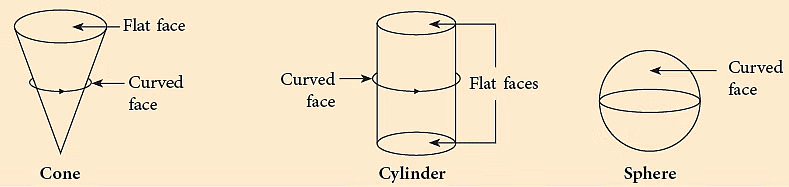 Now, let us find out how many faces, edges and corners does each shape have. For a cube and cuboid, pick up a die and a geometry box and count the number of faces, edges and corners.You will notice that both the cube and cuboid have 6 faces, 12 edges and 8 corners. Now, from the figure given above, try to count the same for cone, cylinder and sphere. You will find that:A cylinder has 3 faces (2 flat, 1 curved), 2 edges and 0 corners.
Now, let us find out how many faces, edges and corners does each shape have. For a cube and cuboid, pick up a die and a geometry box and count the number of faces, edges and corners.You will notice that both the cube and cuboid have 6 faces, 12 edges and 8 corners. Now, from the figure given above, try to count the same for cone, cylinder and sphere. You will find that:A cylinder has 3 faces (2 flat, 1 curved), 2 edges and 0 corners.
A cone has 2 faces (1 flat, 1 curved), 1 edge and 1 corner.
A sphere has only 1 curved surface.
Pyramid
A pyramid is a solid whose base is a polygon and the sides are triangles which meet at the top.
 This is a square pyramid, but there are also triangular pyramids, pentagonal pyramids and so on.A square pyramid has 4 triangular faces and a square face. It has 8 edges and 5 vertices.
This is a square pyramid, but there are also triangular pyramids, pentagonal pyramids and so on.A square pyramid has 4 triangular faces and a square face. It has 8 edges and 5 vertices.
Nets
Net of a Cube
Take a die or any other cube and trace all its faces on a sheet of paper. What is the shape of all the six faces? They are all squares of the same size. Thus, you see that a cube can be made from six squares joined together in a particular manner.
They are all squares of the same size. Thus, you see that a cube can be made from six squares joined together in a particular manner.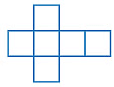 Let us try this combination:
Let us try this combination:
A net is a two-dimensional figure that can be folded into a three-dimensional object.
We have many more nets (arrangements of these squares) that can be folded up to form a cube.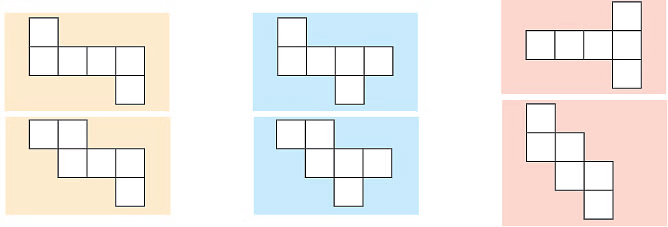 We can also form nets with 5 square faces. In this case it will be a box with no lid.
We can also form nets with 5 square faces. In this case it will be a box with no lid.
Viewing 3d Shapes
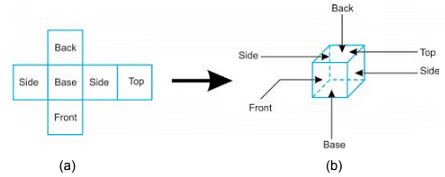
It is difficult to draw a 3D shape. So, designers use the different views of a solid to overcome this problem. A 3D shape can be viewed from the top, from the side and from the front and these views can be combined to visualise what the solid looks like. Thus, we see that a cuboid appears to be rectangle, when viewed from any direction.Now, let us see the different views of a car, which is a 3D shape.
Thus, we see that a cuboid appears to be rectangle, when viewed from any direction.Now, let us see the different views of a car, which is a 3D shape. Special names are given to these three views from different directions.
Special names are given to these three views from different directions.
- When a solid is looked at from above, the view seen is called the Plan.
- The front view is called the Front Elevation.
- The side view is called the Side Elevation.
Examples:
(a) A die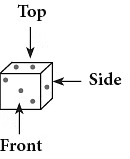 (b) A solid
(b) A solid (c) A tent
(c) A tent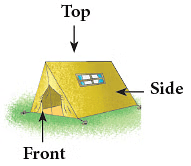 (d)
(d)
Edurev Tips: All the views of a die (cube) are squares.
Reflection and Symmetry
Look at the mirror kept vertically.
The figure in front of the mirror has a reÀection image in the mirror.
See the images of VII and R.
The mirror image and the given original object are exactly symmetrical, the mirror line is the line of symmetry.
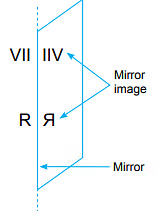
We notice that there is no difference in length or breadth between the object kept in front of the mirror and the image of the object in the mirror.
In this figure, ΔA'B'C' is the mirror image of ΔABC.
We can notice that,
(i) The distances of A', B', C' from the mirror are the same as the distances of A, B and C from the mirror. Farther the point from the mirror line farther will be its mirror image.
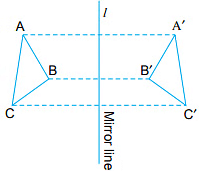
(ii) Also the length of 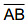 = length of
= length of  Also length of
Also length of 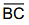 = length of
= length of 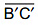 Also length of
Also length of 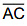 = length of
= length of 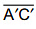 and ∠BAC = ∠B'A'C', ∠ABC = ∠A'B'C', ∠BCA = ∠B'C′A'.(iii) AA', BB' and CC' are perpendicular to the mirror line and are bisected by the mirror line.
and ∠BAC = ∠B'A'C', ∠ABC = ∠A'B'C', ∠BCA = ∠B'C′A'.(iii) AA', BB' and CC' are perpendicular to the mirror line and are bisected by the mirror line.
Mirrors are used in kaleidoscopes to produce images of the small pieces of bangles kept inside. A number of images produced due to the number of mirrors used, give rise to different symmetrical designs in the kaleidoscope.
To Draw A Mirro Image of a Given Figure
Let ABCDE be a figure given to us whose mirror image is to be drawn.
We draw perpendiculars from the vertices of the given figure to the mirror line. AP, E4, DR, CS and BT are drawn perpendiculars to the mirror line.
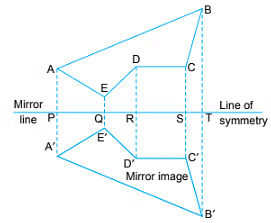
Produce AP to A', E4 to E', DR to D', CS to C', BT to B' such that PA' = PA, QE' = QE, RD' = RD, SC' = SC and TB' = TB. Join A' – B' – C' – D' – E' in sequence to get the mirror image A'B'C'D'E' of the given figure ABCDE.
The mirror line is the line of symmetry between these two figures.
To Complete a Figure With Two Lines of Symmetry
Let ABCDE be the given part of the figure and p, and q be the two lines of symmetry.
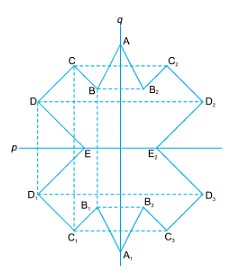
By drawing perpendiculars from the corner points to lines p and q, we get the image points of the corner points of the given part of the figure.
Joining them in sequence, we complete the figure which will have p and q as two lines of symmetry.
Section
Imagine cutting straight through the middle of a cube as shown in the figure.
The cut face (shown shaded in the figure), is called a section of the cube. In this case, the section is a square.
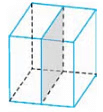
When we make a straight cut through a solid, we say that the solid is cut by a plane, i.e., the section is flat.
Planes of Symmetry
A plane of symmetry divides a 3D shape into two congruent shapes. One shape must be a mirror image of the other shape. A shaded plane is a plane of symmetry of the cube.
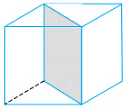
Imagine that a cuboid is cut into two pieces by a plane as shown below.
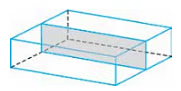
Now take one of the pieces and put the cut face against a mirror.
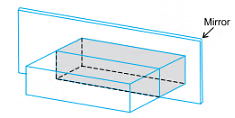
Does the piece, together with its reÀection, look like the complete solid?
If it does, as happens in this case, then the cut has been made in a plane of symmetry.
Not all planes which cut a solid in half are planes of symmetry. The solid below has not been cut in a plane of symmetry. If one half is placed against a mirror, we do not see the complete solid.

Rotational Symmetry
Observe the familiar figures of a line segment, equilateral triangle, square, etc. Besides having linear symmetry, these figures have another type of symmetry which is called rotational symmetry.
Example 1: Draw a line segment AB having a fixed length. Mark its mid-point O. Fix a pin through O. Now, keeping the middle point fixed, rotate the line segment AB about O. After a rotation of 180, you will find that the line segment takes the position B1A1. Thus, new position B1A1 fits into the original line segment AB.

Another rotation of 180 about the central point O gives A1B1, a new position A2B2, once again fitting into the original line segment AB, A2 falling on A and B2 falling on B.
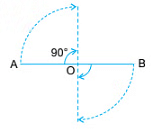
Thus, during one rotation of 360 about the midpoint O, the line segment fits into itself twice (more than once). Therefore, the line segment is said to have rotational symmetry of order 2.
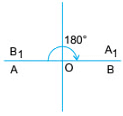
The midpoint of the line segment is the centre of rotation.

The point around which the figure is rotated is called the centre of rotation.
Thus, A figure has rotational symmetry, if there is a central point around which the figure is rotated through a certain number of degrees (less than 180) and the figure still looks the same. The central point is called the centre of rotation. The smallest angle we need to turn the figure to get a similar figure again is called the angle of rotation.
The number of times a shape will fit onto itself in one complete rotation is called the order of the rotational symmetry.
Edurev Tips: A full rotation does not mean that a figure has rotational symmetry because every shape could fit exactly into itself after a full (360º) rotation.
Example 2: Rotate an equilateral triangle about its centroid (the point where the medians meet) through an angle of 120º. After a rotation of 120º, 240º, 360º, the triangle gets three new positions of A1B1C1, A2B2C2 and A3B3C3 falling on BCA, CAB and ABC respectively.
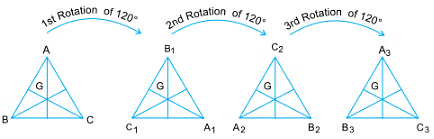
Thus, the triangle matches itself three times during a rotation of 360º. Therefore, it has rotational symmetry of order 3.
Here, the order of rotational symmetry = 360º/120º = 3
Example 3: Rotate a square about its centre (the point where its diagonals meet), through an angle of 90. After each rotation of 90, the new square fits into the original square, i.e., the square matches itself after a rotation of 90, 180, 270 and 360, i.e., 4 times during one complete rotation of 360.

∴ Angle of rotation = 90º
Here, the order of rotation = 360º/90º = 4
In general, we have
Order of rotational symmetry = 360º/the smallest angle of rotation
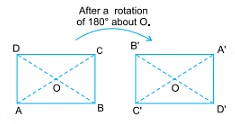
Example 4: A rectangle has rotational symmetry about its centre (the point where its diagonals meet)
Angle of rotation = 180º
∴ Order of rotational symmetry = 360º/180º = 2
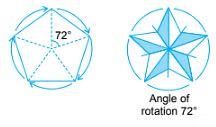
Example 5: A regular pentagon (a polygon having 5 equal sides), a design of flower design with 5 petals are the figures having rotational symmetry of order 5.
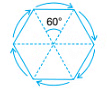
Example 6: A regular hexagon (a polygon having 6 equal sides) has rotational symmetry of order 6 and angle of rotation = 60º.
A regular octagon (a polygon having 8 equal sides) has rotational symmetry of order 8 and angle of rotation = 45º.
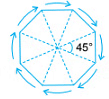
No Rotational Symmetry
If a figure or object can come to its original position only after a rotation of 360º, it does not have any rotational symmetry. For example, a quadrilateral. In fact, every figure can fit into itself after a rotation of 360º.
Figures with Linear Symmetry as well as Rotational Symmetry
Some figures have both types of symmetry, linear as well as rotational.
Consider the following examples :
- An equilateral triangle has linear symmetry having three lines of symmetry. Also, it has rotational symmetry of order 3.
- A rectangle and a rhombus both have a linear symmetry having two lines of symmetry each and rotational symmetry of order 2.
- A square has a linear symmetry having f our lines of symmetry and rotational symmetry of order 4.
All regular figures — pentagon, hexagon, octagon, nonagon, etc., have linear symmetry as well as rotational symmetry. - The letter H of the English alphabet has linear symmetry having two lines of symmetry and rotational symmetry of order 2.
Only Linear Symmetry
There are some figures which have only one line symmetry but have no rotational symmetry.
For example (a) Letters of English alphabet A, C, D, E, M, T, U, 9, W, Y
(b) Isosceles triangle.
Only Rotational Symmetry
We have some figures which have only rotational symmetry but no linear symmetry. For example, letters of the English alphabet N, S, Z.
Nets
If we join together six identical squares, edge to edge, we get a cube or the outside surface of the cube.

We can avoid a lot of unnecessary sticking if we join some squares together before cutting out.
Suppose we want to make a cube out of cardboard or a piece of paper. We need a pattern giving us the shape of the cardboard or the piece of paper to make the cube.
Figure (a) below shows, the shape of the pattern of six squares. When this shape is folded along the edges, a cube is formed as shown.
A cross plan such as shown in figure (a) above, which can be folded to form a cube is called the net of the cube.
A net of a 3D figure is the shape that can be cut out of a flat piece of paper or cardboard and folded to make the 3D shape.
There are other arrangements of six squares that can be folded up to make a cube. For example, a cube can also be made from the nets shown below.

However, not all arrangements of six squares will work as shown below :

It is easy to make a solid shape from a piece of paper or cardboard by first drawing a net of the faces of the solid. The net can be made up of different plane shapes (rectangles, squares, triangles).
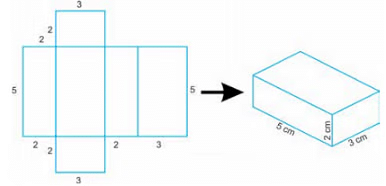
The figure below shows the net of a cuboid of dimensions 5 cm × 3 cm × 2 cm.
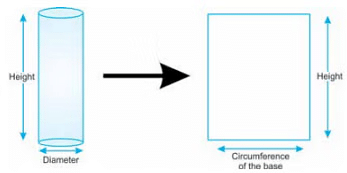
The net for a cylinder without a top and a bottom is shown. The length of the net is equal to the circumference of the cylinder.
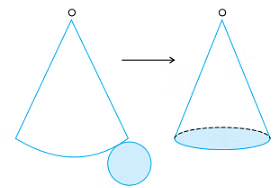
The net of a cone has one circular base and one curved surface.
|
41 videos|151 docs|72 tests
|
FAQs on Notes: Solids Around Us - Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET
| 1. What are some examples of solids around us that can be studied in the context of geometry? |  |
| 2. How are nets used in geometry to represent 3D shapes? |  |
| 3. How can rotational symmetry be identified in a solid shape? |  |
| 4. How do planes of symmetry play a role in understanding the symmetry of a solid shape? |  |
| 5. What is the significance of reflection and symmetry in the study of 3D shapes? |  |





















