Notes: Two Port Analysis | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download
In electronics, a two-port network (also known as a four-terminal network or quadripole) is an electrical circuit or device with two pairs of terminals for connecting to external circuits. A pair of terminals forms a port if the currents entering and exiting the terminals satisfy the port condition: the current entering one terminal must equal the current leaving the other terminal of the same port. These ports serve as the interfaces where the network connects to other networks, allowing signals to be applied or outputs to be taken. Typically, in a two-port network, port 1 is the input port and port 2 is the output port.
The first and second ports are called as port1 and port2 respectively.
One port network is a two terminal electrical network in which, current enters through one terminal and leaves through another terminal. Resistors, inductors and capacitors are the examples of one port network because each one has two terminals. One port network representation is shown in the following figure. Here, the pair of terminals, 1 & 1’ represents a port. In this case, we are having only one port since it is a one port network.
Here, the pair of terminals, 1 & 1’ represents a port. In this case, we are having only one port since it is a one port network.
Similarly, two port network is a pair of two terminal electrical network in which, current enters through one terminal and leaves through another terminal of each port. Two port network representation is shown in the following figure.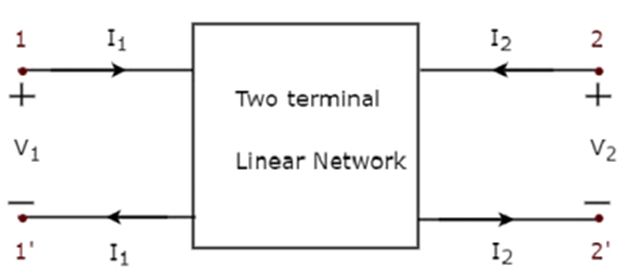 Here, one pair of terminals, 1 & 1’ represents one port, which is called as port1 and the other pair of terminals, 2 & 2’ represents another port, which is called as port2.
Here, one pair of terminals, 1 & 1’ represents one port, which is called as port1 and the other pair of terminals, 2 & 2’ represents another port, which is called as port2.
There are four variables V1, V2, I1 and I2 in a two port network as shown in the figure. Out of which, we can choose two variables as independent and another two variables as dependent. So, we will get six possible pairs of equations. These equations represent the dependent variables in terms of independent variables. The coefficients of independent variables are called as parameters. So, each pair of equations will give a set of four parameters.
Two Port Network Parameters
The parameters of a two port network are called as two port network parameters or simply, two port parameters. Following are the types of two port network parameters.
Now, let us discuss about these two port network parameters one by one.
Z parameters
We will get the following set of two equations by considering the variables V1 & V2 as dependent and I1 & I2 as independent. The coefficients of independent variables, I1 and I2 are called as Z parameters.
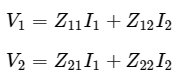
The Z parameters are
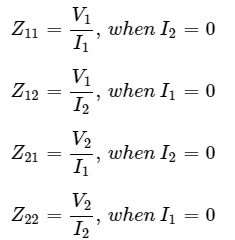
Z parameters are called as impedance parameters because these are simply the ratios of voltages and currents. Units of Z parameters are Ohm (Ω).
We can calculate two Z parameters, Z11 and Z21, by doing open circuit of port2. Similarly, we can calculate the other two Z parameters, Z12 and Z22 by doing open circuit of port1. Hence, the Z parameters are also called as open-circuit impedance parameters.
Y parameters
We will get the following set of two equations by considering the variables I1 & I2 as dependent and V1 & V2 as independent. The coefficients of independent variables, V1 and V2 are called as Y parameters.
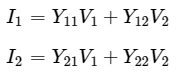
The Y parameters are
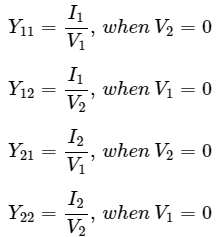
Y parameters are called as admittance parameters because these are simply, the ratios of currents and voltages. Units of Y parameters are mho.
We can calculate two Y parameters, Y11 and Y21 by doing short circuit of port2. Similarly, we can calculate the other two Y parameters, Y12 and Y22 by doing short circuit of port1. Hence, the Y parameters are also called as short-circuit admittance parameters.
T parameter
We will get the following set of two equations by considering the variables V1 & I1 as dependent and V2 & I2 as independent. The coefficients of V2 and -I2 are called as T parameters.
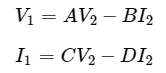
The T parameters are 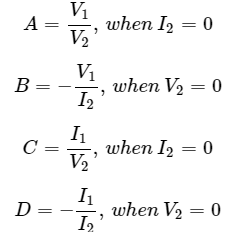
T parameters are called as transmission parameters or ABCD parameters. The parameters, A and D do not have any units, since those are dimension less. The units of parameters, B and C are ohm and mho respectively.
We can calculate two parameters, A and C by doing open circuit of port2. Similarly, we can calculate the other two parameters, B and D by doing short circuit of port2.
T ’ parameters
We will get the following set of two equations by considering the variables V2 & I2 as dependent and V1 & I1 as independent. The coefficients of V1 and -I1 are called as T’ parameters.
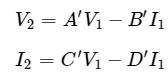
The T’ parameters are 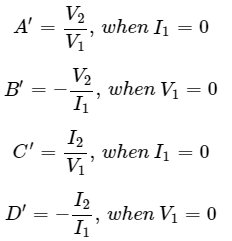
T’ parameters are called as inverse transmission parameters or A’B’C’D’ parameters. The parameters A’ and D’ do not have any units, since those are dimension less. The units of parameters, B’ and C’, are Ohm and Mho respectively.
We can calculate two parameters, A’ and C’, by doing an open circuit of port1. Similarly, we can calculate the other two parameters, B’ and D’, by doing a short circuit of port1.
h-parameters
We will get the following set of two equations by considering the variables V1 & I2 as dependent and I1 & V2 as independent. The coefficients of independent variables, I1 and V2, are called as h-parameters.
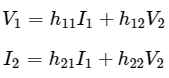 The h-parameters are
The h-parameters are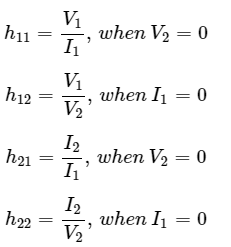
h-parameters are called as hybrid parameters. The parameters, h12 and h21, do not have any units, since those are dimension-less. The units of parameters, h11 and h22, are Ohm and Mho respectively.
We can calculate two parameters, h11 and h21 by doing short circuit of port2. Similarly, we can calculate the other two parameters, h12 and h22 by doing open circuit of port1.
The h-parameters or hybrid parameters are useful in transistor modelling circuits (networks).
g-parameters
We will get the following set of two equations by considering the variables I1 & V2 as dependent and V1 & I2 as independent. The coefficients of independent variables, V1 and I2 are called as g-parameters.  The g-parameters are
The g-parameters are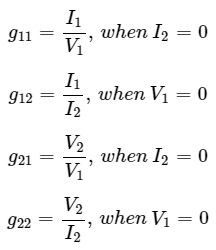 g-parameters are called as inverse hybrid parameters. The parameters, g12 and g21 do not have any units, since those are dimension less. The units of parameters, g11 and g22 are mho and ohm respectively.
g-parameters are called as inverse hybrid parameters. The parameters, g12 and g21 do not have any units, since those are dimension less. The units of parameters, g11 and g22 are mho and ohm respectively.
We can calculate two parameters, g11 and g21 by doing open circuit of port2. Similarly, we can calculate the other two parameters, g12 and g22 by doing short circuit of port1.
Sometimes, it is easy to find one set of parameters of a given electrical network easily. In those situations, we can convert these parameters into the required set of parameters instead of calculating these parameters directly with more difficulty.
Procedure of two port parameter conversions
Follow these steps, while converting one set of two port network parameters into the other set of two port network parameters.
- Step 1 − Write the equations of a two port network in terms of desired parameters.
- Step 2 − Write the equations of a two port network in terms of given parameters.
- Step 3 − Re-arrange the equations of Step2 in such a way that they should be similar to the equations of Step1.
- Step 4 − By equating the similar equations of Step1 and Step3, we will get the desired parameters in terms of given parameters. We can represent these parameters in matrix form.
Z parameters to Y parameters
Here, we have to represent Y parameters in terms of Z parameters. So, in this case Y parameters are the desired parameters and Z parameters are the given parameters.
Step 1 − We know that the following set of two equations, which represents a two port network in terms of Y parameters.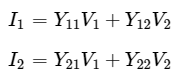 We can represent the above two equations in matrix form as
We can represent the above two equations in matrix form as
Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters. 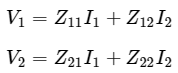
We can represent the above two equations in matrix form as 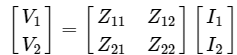 Step 3 − We can modify it as
Step 3 − We can modify it as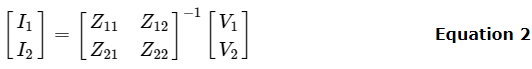 Step 4 − By equating Equation 1 and Equation 2, we will get
Step 4 − By equating Equation 1 and Equation 2, we will get 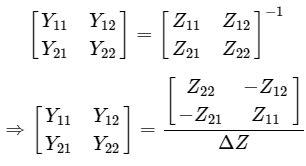 Where,
Where, 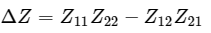 So, just by doing the inverse of Z parameters matrix, we will get Y parameters matrix.
So, just by doing the inverse of Z parameters matrix, we will get Y parameters matrix.
Z parameters to T parameters
Here, we have to represent T parameters in terms of Z parameters. So, in this case T parameters are the desired parameters and Z parameters are the given parameters.
Step 1 − We know that, the following set of two equations, which represents a two port network in terms of T parameters.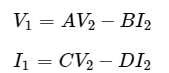
Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters.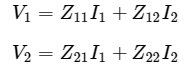 Step 3 − We can modify the above equation as
Step 3 − We can modify the above equation as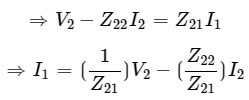 Step 4 − The above equation is in the form of I1=CV2−DI2 . Here,
Step 4 − The above equation is in the form of I1=CV2−DI2 . Here,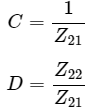 Step 5 − Substitute I1 value of Step 3 in V1 equation of Step 2.
Step 5 − Substitute I1 value of Step 3 in V1 equation of Step 2.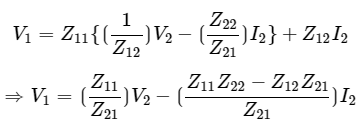
Step 6 − The above equation is in the form of V1=AV2−BI2 . Here,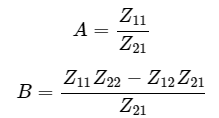
Step 7 − Therefore, the T parameters matrix is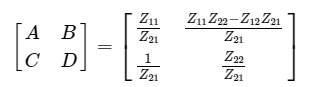
Y parameters to Z parameters
Here, we have to represent Z parameters in terms of Y parameters. So, in this case Z parameters are the desired parameters and Y parameters are the given parameters.
Step 1 − We know that, the following matrix equation of two port network regarding Z parameters as Step 2 − We know that, the following matrix equation of two port network regarding Y parameters as
Step 2 − We know that, the following matrix equation of two port network regarding Y parameters as  Step 3 − We can modify it as
Step 3 − We can modify it as Step 4 − By equating Equation 3 and Equation 4, we will get
Step 4 − By equating Equation 3 and Equation 4, we will get 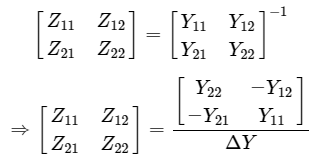 Where,
Where,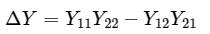 So, just by doing the inverse of Y parameters matrix, we will get the Z parameters matrix.
So, just by doing the inverse of Y parameters matrix, we will get the Z parameters matrix.
Y parameters to T parameters
Here, we have to represent T parameters in terms of Y parameters. So, in this case, T parameters are the desired parameters and Y parameters are the given parameters.
Step 1 − We know that, the following set of two equations, which represents a two port network in terms of T parameters.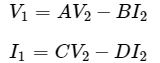
Step 2 − We know that the following set of two equations of two port network regarding Y parameters.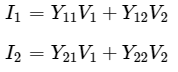
Step 3 − We can modify the above equation as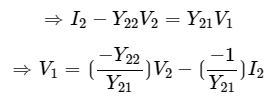 Step 4 − The above equation is in the form of V1=AV2−BI2 . Here,
Step 4 − The above equation is in the form of V1=AV2−BI2 . Here,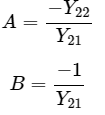 Step 5 − Substitute V1 value of Step 3 in I1 equation of Step 2.
Step 5 − Substitute V1 value of Step 3 in I1 equation of Step 2.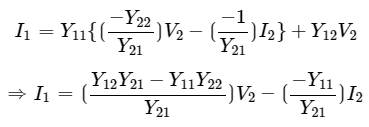
Step 6 − The above equation is in the form of I1=CV2−DI2 . Here,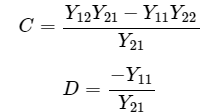 Step 7 − Therefore, the T parameters matrix is
Step 7 − Therefore, the T parameters matrix is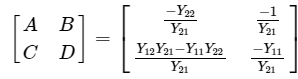
T parameters to h-parameters
Here, we have to represent h-parameters in terms of T parameters. So, in this case hparameters are the desired parameters and T parameters are the given parameters.
Step 1 − We know that, the following h-parameters of a two port network.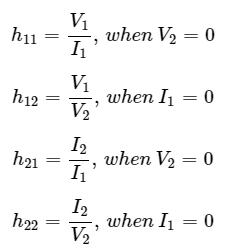 Step 2 − We know that the following set of two equations of two port network regarding T parameters.
Step 2 − We know that the following set of two equations of two port network regarding T parameters. Step 3 − Substitute V2=0 in the above equations in order to find the two h-parameters, h11 and h21 .
Step 3 − Substitute V2=0 in the above equations in order to find the two h-parameters, h11 and h21 . Substitute, V1 and I1 values in h-parameter, h11.
Substitute, V1 and I1 values in h-parameter, h11. Substitute I1 value in h-parameter h21 .
Substitute I1 value in h-parameter h21 .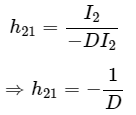
Step 4 − Substitute I1=0 in the second equation of step 2 in order to find the h-parameter h22 .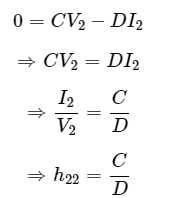 Step 5 − Substitute
Step 5 − Substitute  in the first equation of step 2 in order to find the h-parameter, h12 .
in the first equation of step 2 in order to find the h-parameter, h12 .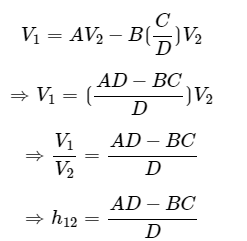 Step 6 − Therefore, the h-parameters matrix is
Step 6 − Therefore, the h-parameters matrix is 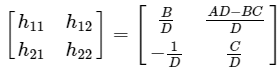
h-parameters to Z parameters
Here, we have to represent Z parameters in terms of h-parameters. So, in this case Z parameters are the desired parameters and h-parameters are the given parameters.
Step 1 − We know that, the following set of two equations of two port network regarding Z parameters.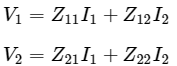 Step 2 − We know that, the following set of two equations of two-port network regarding h-parameters.
Step 2 − We know that, the following set of two equations of two-port network regarding h-parameters. Step 3 − We can modify the above equation as
Step 3 − We can modify the above equation as 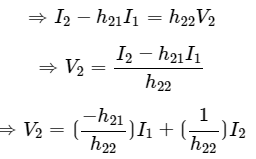 The above equation is in the form of
The above equation is in the form of 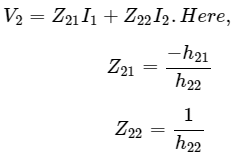
Step 4 − Substitute V2 value in first equation of step 2.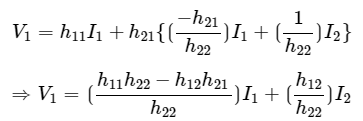
The above equation is in the form of V1=Z11I1+Z12I2 . Here,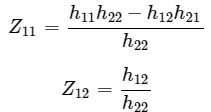 Step 5 − Therefore, the Z parameters matrix is
Step 5 − Therefore, the Z parameters matrix is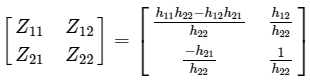
In this way, we can convert one set of parameters into other set of parameters.
Application of Two Port Analysis
Purpose and Usage:
- The two-port network model is utilized in mathematical circuit analysis to isolate specific parts of larger circuits.
- It treats a portion of the circuit as a "black box," defined by a matrix of numbers.
Advantages:
- Simplifies the calculation of the network's response to signals applied to the ports.
- Eliminates the need to solve for all internal voltages and currents within the network.
- Facilitates easy comparison of similar circuits or devices.
Applications:
- Commonly applied to devices like transistors, which are characterized by parameters (e.g., h-parameters) provided by manufacturers.
- Can be used for any linear circuit with four terminals, as long as it does not contain an independent source and satisfies the port conditions.
Examples of Analyzed Circuits:
- Filters
- Matching networks
- Transmission lines
- Transformers
- Small-signal transistor models (e.g., hybrid-pi model)
Historical Context:
- The analysis of passive two-port networks is based on reciprocity theorems first derived by Lorentz.
Mathematical Representation:
- Described by a 2x2 matrix of complex numbers.
- Various parameter models include z-parameters, y-parameters, h-parameters, g-parameters, and ABCD-parameters.
- Each model differs based on which variables (voltage or current) are considered independent.
Parameters and Variables:
- V1: Voltage across port 1
- I1: Current into port 1
- V2: Voltage across port 2
- I2: Current into port 2
Model Differences:
- Different models are used depending on which variables (voltage or current) are considered the independent variables.
Frequency Considerations:
- Current and voltage variables are most useful at low-to-moderate frequencies.
- At high frequencies (e.g., microwave frequencies), power and energy variables are more appropriate.
- The traditional current-voltage approach is replaced by scattering parameters at high frequencies.
|
73 videos|139 docs|62 tests
|
FAQs on Notes: Two Port Analysis - Network Theory (Electric Circuits) - Electrical Engineering (EE)
| 1. What are the different types of two-port network parameters? |  |
| 2. How can Z parameters be converted to Y parameters? |  |
| 3. What is the significance of two-port network analysis in electronic circuits? |  |
| 4. Can Y parameters be used to analyze the behavior of passive circuits? |  |
| 5. How do T parameters differ from h-parameters in two-port network analysis? |  |






















