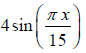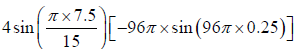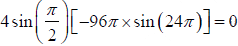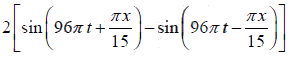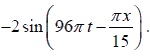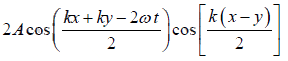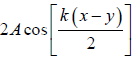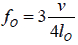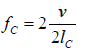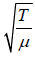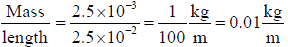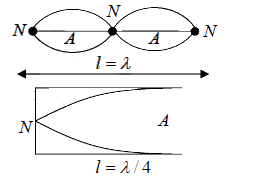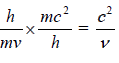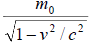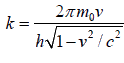Notes: Wave Motion | General Awareness - Bank Exams PDF Download
A wave is defined as a oscillatory disturbance of particle in the medium which distribute
energy from one particle to other particle.
In general there are only two types of waves one which required material medium to
travel while other travel in vacuum also. The former is called mechanical wave and later
is called electromagnetic wave.
Mechanical Wave
Water wave, sound wave, ultrasound wave, earthquake wave etc
Electromagnetic wave
Radio wave, Microwave, Infrared wave, light wave etc.
There are two distinct classes of wave
- Transverse wave and
- Longitudinal wave
Transverse wave
In the transverse wave motion the oscillation of the particles is at right angle to the
direction of propagation of the wave.
Example: Wave generated in rope and stretched string, electromagnetic wave, water
wave, earthquake wave etc.
Longitudinal Wave
In the longitudinal wave the oscillation of the particle is the same as the direction of
propagation of the wave.
Example: Sound wave, ultrasound wave etc.
Wave Front
A plane or a surface on which all the particles of the medium are in an identical state of
motion at a given instant, i.e. in same phase, is called a wave front.
In homogeneous and isotropic medium, the wave front is always perpendicular to the
direction of the propagation of wave. Wave front although have various shape but the two
most important shapes are Plane Wave Front and Spherical Wave Front.
Traveling Waves
Let’s start with a rope, like a clothesline, stretched between two hooks. You take one end
off the hook, holding the rope, and, keeping it stretched fairly tight, wave your hand up
and back once. If you do it fast enough, you’ll see a single bump travel along the rope:
This is the simplest example of a traveling wave.

Taking the rope to be stretched tightly enough that we can take it to be horizontal, we’ll
use it as x -axis. The y -axis is taken vertically upwards, and we only wave the rope in an
up-and-down way, so actually y (x,t ) will be how far the rope is from its rest position at
x at time t : that is, the graph y (x,t ) above just shows where the rope is at time t .
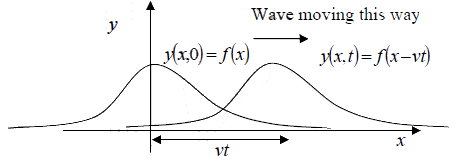
Taking for convenience time t = 0 to be the moment when the peak of the wave passes
x = 0 , we graph here the rope’s position at t = 0, and some later time t . Denoting the first
function by y (x,0) = f (x) , than the displacement y of the rope at any horizontal position
at x at time t has the form
y (x,t ) = f (x − vt )
it’s the same function—the “same shape”—but moved over by vt , where v is the
velocity of the wave in the positive x axis.
Expression for a Plane Progressive Harmonic Wave
Wave equation can be expressed in following types y = 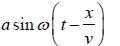
In term of time period T = 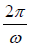 and wavelength λ = vT is y =
and wavelength λ = vT is y = 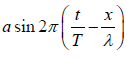
In term of wave vector k = 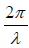 is y =
is y = 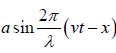 or y = a sin k (vt − x)
or y = a sin k (vt − x)
or y = a sin (ωt − kx)
Differential Equation of Wave Motion
We have the equation of plane progressive wave motion is
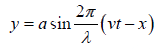
acceleration of the particle = 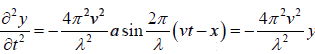
Also, rate of change of compression with distance can be obtain as
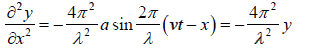
Combining above two equation, we get
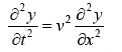
This is the differential equation for one dimensional wave motion. We can also write
particle acceleration = (wave velocity)2 ×curvature of the displacement curve.
Energy Density of the Plane progressive Wave
In a progressive wave motion, energy from the source is passed from particles to other
particles. There is a regular transmission of energy across every section of the medium.
Energy density of plane progressive wave = total energy = {kinetic energy (K.E) + potential energy (P.E.)} per unit volume of the medium.
Let ρ is the density of the medium in which wave is moving.
Thus the kinetic energy per unit volume Kρ is obtained as
K.E.= 1/2 (mass)(velocity)2 = 1/2(density x velocity)(velocity)
Kρ = K.E./Volume = 1/2 (density)(velocity)2 = 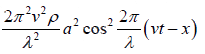
The potential energy per unit volume Uρ is obtained as
Force acting per unit volume = density × acceleration = 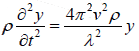
Now, work done per unit volume in a small displacement
dy = Force per unit volume x displacement = 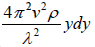
Work done per unit volume for whole displacement from 0 to y
= 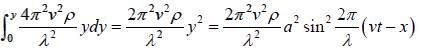
This work done is stored in the medium in the form of potential energy.
Thus Uρ = P.E. per unit volume = 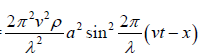
The total energy per unit volume of the medium or the energy density of the plane
progressive wave is Eρ = Kρ + Uρ
Eρ = 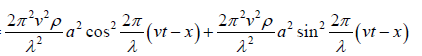
= 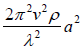 =
=  Where, f is the frequency of the wave.
Where, f is the frequency of the wave.
Stationary Waves
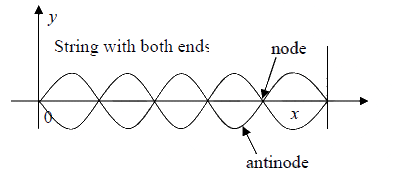
Another familiar kind of wave is that generated on a string fixed at both ends when it is
made to vibrate. We found in class that for certain frequencies the string vibrated in a
sine-wave pattern, as illustrated below, with no vibration at the ends, of course, but also
no vibration at a series of equally-spaced points between the ends: these quiet places we
term nodes. The places of maximum oscillation are antinodes.
Almost all musical instruments generate standing waves: the piano has standing waves on strings, the organ generates standing waves in the air in pipes. Other instruments are more complicated: although the sound of a violin comes from a vibrating string, resonance with the rest of the instrument gives rise to complicated standing wave patterns.
When two identical wave either longitudinal or transverse, travel through a medium along the same line in opposite direction, they superimpose to produce a wave which appears to be stationary in space. Such waves are called stationary wave or standing wave.
Condition for Stationary waves
The presence of bounded medium is prerequisite for producing stationary wave. Medium
should not be infinite in length, it should have boundary.
If the medium is infinite, the wave just continues to travel along it for an infinite time, i.e.
such medium support travelling wave.
General Consideration of Stationary Wave
Consider a plane progressive wave of amplitude a travelling with velocity v along the
+x axis. Its equation is written as y1= 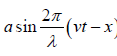
where, y1 is the displacement at a point x at a time t and a is the amplitude.
If this wave is reflected from a rigid boundary wall situated at x = 0 . The displacement
y2 of the reflected wave will be y2 = 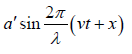
Where, a′ is the amplitude of the reflected wave.
Both the wave travelling in the same linear path superimpose and the equation of the
resultant wave is y = y1 + y2 = 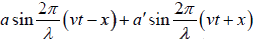
The displacement y at rigid wall (at x = 0 ) will always be zero. This give the boundary
condition, y = 0 at x = 0 .
Thus 0 =  ⇒ a = −a′
⇒ a = −a′
Thus the resultant displacement is
y = 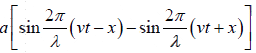 =
= 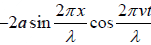 ⇒ y = −2asin kx cosωt
⇒ y = −2asin kx cosωt
This is the equation of the resultant stationary wave. Equation shows that the resulting
wave is also a simple harmonic wave of the same time period and wavelength but with
the amplitude of −2a sin kx .
The particle velocity is
The resultant pressure variation is
p = 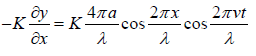
Let us now consider the changes that occur,
(a) with respect to position of a particle, (b) with respect to time.
(a) Changes with respect to position
(i) At point where
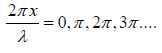 or
or 
we have sin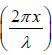 = 0 and cos
= 0 and cos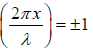
At these values of x ; Displacement ( y) = 0 , velocity (u) = 0 , while the pressure ( p) is
maximum (alternatively positive and negative) relative to all other points. These points
are called NODES and are separated from each other by λ/2.
(ii) At point where
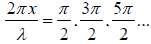 or
or 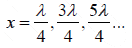
We have sin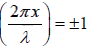 and cos
and cos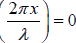
At these values of x ; Displacement ( y) and velocity (u) is always maximum, while the
pressure variation ( p) is always zero relative to all other points. These points are called
ANTINODES and are separated from each other by λ/2.
(b) Changes with respect to time
(i) At a time when
 or t =
or t = 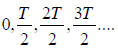
We have sin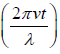 = 0 and cos
= 0 and cos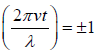
At these points, the displacement y and pressure variation p are maximum while velocity
u is zero relative to all other times. Such instant occur twice in each period
(ii) At a time when
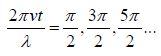 or t =
or t = 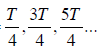
We have sin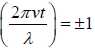 and cos
and cos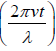 = 0
= 0
At these points, the displacement y and pressure variation p are zero while velocity u is
maximum relative to all other times. Such instant occur twice in each period.
Note: Superposition of incident and reflected wave produce a stationary weaves
characterized by nodes which remains permanently at rest but suffer maximum pressure
variation, and the antinodes which have maximum displacement but suffer minimum
pressure variation.
We now, are going to discuss the formation of stationary wave and excitation of different
frequency modes in following different three cases.
- When both the boundaries are rigid
- When one boundary is rigid and other is free
- When both the boundaries are free
Case I: When both the boundaries of the medium are rigid
Let two wave travelling in the same linear path in opposite direction in medium of
length l, superimpose and the equation of the resultant wave is
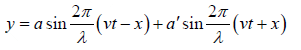
First boundary condition: the displacement y = 0 at x = 0 . This gives
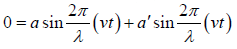 ⇒a = −a′
⇒a = −a′
Thus the resultant displacement is y = 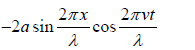
This is the expression of standing wave
Second boundary condition: the displacement y = 0 at x = l . this gives
0 = 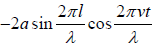
This must be true for all values of t, thus
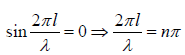 ⇒ λ = 2l/n where n = 0,1,2,3....
⇒ λ = 2l/n where n = 0,1,2,3....
The allowed frequencies in such medium is f = 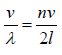
This shows that the when medium has rigid boundaries at both end, it sustain vibration of
certain discrete frequencies such as f = 
These frequencies are the normal frequencies or modes of vibration. The lowest
frequency is the fundamental frequency. Since frequencies are in harmonic series, they
are also called Harmonics.
Conclusion: In a linear bounded medium when both the boundaries are rigid, all the
harmonics even and odd are present.
Case II: When one boundary of the medium is rigid and other is free
Consider that boundary is rigid at x = 0 , and the other boundary is free at x = l . The
boundary conditions for such medium is y = 0 at x = 0 and pressure p =  = 0
= 0
at x = l .
The equation of the resultant wave is y = 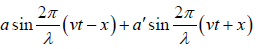
First boundary condition: the displacement y = 0 at x = 0 . This gives
0 = 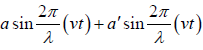 ⇒a = −a′
⇒a = −a′
Thus the resultant displacement is y = 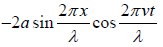
The resultant pressure variation is p = 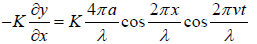
Second boundary condition: p = 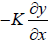 = 0 at x = l , we get
= 0 at x = l , we get
0 = 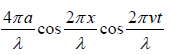
This must be true for all values of t, thus
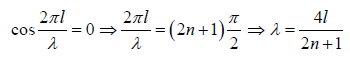 where n = 0,1,2,3....
where n = 0,1,2,3....
The allowed frequencies are f = 
The fundamental frequency is v/4l and the higher frequencies are odd multiples of it.
Conclusion: In a linear bounded medium when one boundary is rigid and other free, only odd harmonics are present.
Case III: When both the boundaries are free
Consider a medium with free boundaries at x = 0 and at x = l . The boundary conditions
for such medium are pressure p = 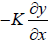 = 0 at x = 0 and at x = l . The equation of the
= 0 at x = 0 and at x = l . The equation of the
resultant wave is y = 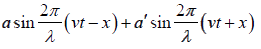
The pressure variation is
p = 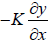 =
= 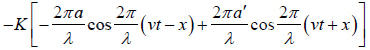
First boundary condition: p = 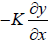 = 0 at x = 0 , we get
= 0 at x = 0 , we get
0 = 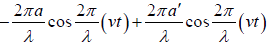 ⇒this gives a = a′
⇒this gives a = a′
Thus the resultant wave is
y =  =
= 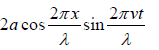
The resultant pressure variation is p = 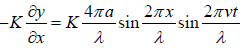
Second boundary condition: p 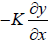 = 0 at x = l , we get
= 0 at x = l , we get
0 = 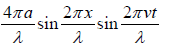
This must be true for all values of t , thus
 ⇒ λ = 2l / n where n = 0,1,2,3....
⇒ λ = 2l / n where n = 0,1,2,3....
The allowed frequencies in such medium is f = 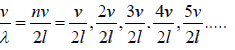
The fundamental frequency is v/2l and the higher frequencies are integral multiple of it.
Conclusion: In a linear bounded medium when both boundaries are free, all the
harmonics are present.
Example 1: The vibrations of a string of length 60 cm fixed at both ends are represented by the equation y = 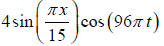 where x and y are in cm and t in second.
where x and y are in cm and t in second.
(i) What is the maximum displacement of a point at x = 5cm?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at x = 7.5cm, t = 0.25sec ?
(iv) Write down the equations of the component waves whose superposition gives the above wave.
(i) The equation represents a stationary wave having amplitude A =
At x = 5, amplitude =
= 2√3 = 3.46cm (1)
(ii) Nodes along string:
At nodes, amplitude A = 0 ∴
= 0 ⇒ πx/15 = nπ where n = 0,1,2,....
or x =15n or x = 0, 15cm, 30cm, 60cm.
(iii) Velocity of particle:
y =
∴ dy/dt =
At x = 7.5cm,t = 0.25sec .,
v =
∴ Velocity =
(iv) Component waves:
y =
or y =
or y =
∴ The two component waves are
y1 =and y2 =
Example 2: The following equations represent transverse waves:
z1 = Acos(kx −ωt); z2 = Acos (kx +ωt) ; z3 = Acos (ky −ωt)
Identify the combination of the waves which will produce
(i) standing wave, (ii) a wave travelling in the direction making an angle 45o with the
positive x and positive y axes.
In each case, find the positions at which the resultant intensity is always zero.
z1 = Acos(kx −ωt) represents a wave travelling along positive x -axis.
z2 = Acos (kx +ωt) represents a wave travelling along negative x -axis.
z3 = Acos (ky −ωt) represents a wave travelling along positive y -axis.
(i) Standing waves
z1 and z2 denote waves travelling in opposite directions along x -axis. They superpose to produce standing waves.
z = z1 + z2 or z = 2Acos kx cosωt
Amplitude of stationary waves = (2Acos kx)
For resultant intensity to be zero, 2Acos kx = 0 or x =
where n = 0,1,2,....
(ii) A wave at 45o:
By superposition of z1 and z3 , a wave will be formed which will travel in the direction making an angle of 45o with the positive x and positive y axes.
∴ z = z1 + z3
or z = Acos(kx −ω t ) + Acos (ky −ω t )
or z =
∴ Amplitude of resultant wave =
For resultant intensity to be zero
= 0 or (x + y ) =
where n = 0,1,2,...
Longitudinal Waves
In a longitudinal wave, particles of the medium are displaced in a direction parallel to energy transport.
Longitudinal waves include sound waves, seismic P-waves, ultrasound wave etc. Sound waves in air (and any fluid medium) are longitudinal waves because particles of the medium through which the sound is transported vibrate parallel to the direction that the sound wave moves.
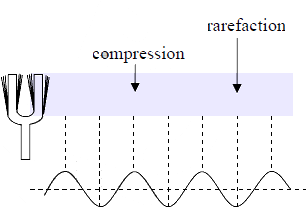
The sound wave traveling through air will cause a sinusoidal pressure variation in the air. The air motion which accompanies the passage of the sound wave will be back and forth in the direction of the propagation of the sound. These back and forth vibrations are imparted to adjacent neighbors by particle-to-particle interaction. Other surrounding particles begin to move rightward and leftward, thus sending a wave to the right. Since air molecules (the particles of the medium) are moving in a direction that is parallel to the direction that the wave moves, the sound wave is referred to as a longitudinal wave. The result of such longitudinal vibrations is the creation of compressions and rarefactions within the air.
Longitudinal Wave as a Pressure Wave
The displacement equation for plane wave travelling in the +x direction with velocity v is y = 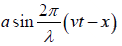
If p is the instantaneous change in pressure at a point x , then p = 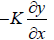
Where, K is the Bulk modulus of elasticity of the medium
p = 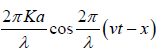
Longitudinal wave velocity in a medium of density is v = 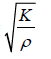
Thus p = 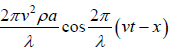 =
= 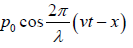
This is the pressure equation of longitudinal wave.
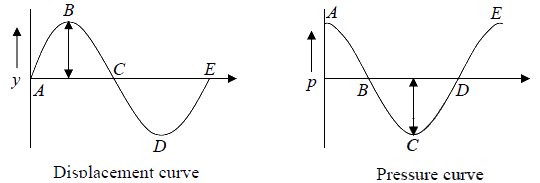
Velocity of the Longitudinal Waves
Velocity of the Longitudinal Waves in solid
When a metallic rod is excited longitudinally by stroking it lengthwise, its cross-sections
oscillate to and fro in the direction of the length of the rod and longitudinal waves are set
up. The velocity of these waves depends upon the density and elastic modulus of the
material. If Y is the young modulus and ρ is the density of the material, than the
velocity of longitudinal wave is v = 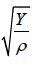
The velocity of sound in a rod of Nickel Y = 21.4×1010 Nm−2 and ρ = 8.9×103 kgm−3 is
v = 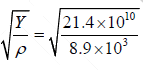 = 4900 ms-1
= 4900 ms-1
Thus the speed of sound in solids is quite high.
Velocity of the Longitudinal Waves in Gas
When longitudinal wave such as sound wave travel in gas, its particle oscillate in the
direction of wave propagation. The result of such longitudinal vibrations is the creation of
compressions and rarefactions within the air. Therefore pressure varies from particle to
particle in the gas. If K is the Bulk modulus of the gas and ρ is the density, then the
velocity of the sound wave in gas is v = 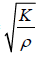
The Bulk modulus K is defined as K = stress/strain = 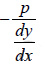
The negative sign indicate that when pressure increases, the volume decreases.
Newton’s Correction
Newton assumed that the propagation of sound wave in a gas is an isothermal process.
Thus for a given mass of gas at pressure P and volume V , we have from Boyle’s Law.
PV = constant (isothermal change)
On differentiating we get
PdV +VdP = 0 ⇒ P = 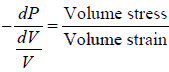 = K (Bulk modulus)
= K (Bulk modulus)
Thus the velocity of the sound in gas become v = 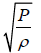 .
.
Newton’s result did not produce exact result of the sound velocity. As if we substitute the
values of standard temperature and pressure (STP), density ρ =1.29 kgm−3 and Pressure
P = 0.76 mm of Hg = 0.76×(13.6×103 )×9.8 Nm−2 .We get v = 280 m/ sec while the
experimental value is 332 m/ s . Newton was unable to explain this discrepancy. Thus
another correction was made by Laplace in the expression.
Laplace Correction
Laplace suggested that propagation of sound wave in air is an adiabatic process and not
an isothermal as pointed by Newton’s. According to Laplace, gases are bad conductor of
heat. Since the compression and rarefaction occurs very fast, therefore the heat developed at compression can-not go into surrounding and no heat from surrounding comes to rarefaction. Hence, the air in the path of sound wave suffers temperature change, or we can say that the conditions are adiabatic.
Thus the relation between pressure and volume for adiabatic system is PVγ = constant ,
where γ is the adiabatic factor and defined as ratio heat capacity at constant pressure and
volume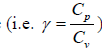 . Now differentiating the PVγ = constant , we get
. Now differentiating the PVγ = constant , we get
PγVγ-1dV + VγdP = 0 ⇒ γP =  = K (Bulk modulus)
= K (Bulk modulus)
Thus the velocity of sound in gas is v = 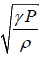
This is Laplace corrected sound velocity. By taking, γ =1.41 for air, velocity of sound at
STP is v = 331 m/ s , which is close to the actual value.
Effect of Temperature on Sound Velocity in Gases
The density of a gas is ρ = 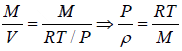
Where, R is the gas constant. The velocity of sound can be written as v = 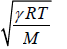
Thus the velocity of sound in a gas
- is independent of pressure or density,
- is proportional to the square root of the absolute temperature of the gas
- is inversely proportional to square root of the molecular weight of the gas
- and depends on the value of γ of a gas, i.e. whether gas is mono-atomic, diatomic etc.
Example 3: The air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency 440Hz . The speed of sound in air is330ms−1.
End corrections may be neglected. Find the length L of the air column.
At second overtone L = 5λ / 4, ⇒ L = 5/4 x velocity/frequency
⇒ L =
⇒ L = 15/16m
Example 4: The first overtone of an open organ pipe beats with the first overtone of a closed organ pipe with a beat frequency of 2.2 Hz . The fundamental frequency of the closed organ pipe is110Hz . Find the lengths of the pipes. (speed of sound is 330m/ s )
Frequency of the first overtone for a open pipe is
Frequency of the first overtone of a closed pipe is
Fundamental frequency of the closed pipe
= 1.5m
First case: let fc > fo ; ∴ fc - fo = 2.2 ⇒ 220-
= 2.2 ⇒ lo = 1.14m
Second: let fc > fo ; ∴ fc - fo = 2.2 ⇒
- 220 = 2.2 ⇒ lo = 1.11m
Transverse Wave
Velocity of Transverse Waves in a Stretched String
When a infinitely thin, uniform and perfectly flexible string is displaced at any point and
left, transverse waves starts moving from that point along both sides of the string with
certain velocity. The whole string vibrates at right angle to its length and the tension in
the string provides the restoring force necessary for vibration.
Transverse wave velocity in a stretched string is v = 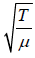 , where T is the tension in the string and μ is mass per unit length.
, where T is the tension in the string and μ is mass per unit length.
Velocity expression shows that it is independent of wavelength i.e. waves of all wavelength travels with the same velocity in a given stretched string.
Let us consider a string of mass 1.0 gm−1 is stretched with a force of 10N . The velocity
of transverse wave in string is v = 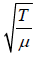 =
= 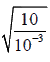 = 100 ms-1
= 100 ms-1
Normal Modes of Oscillations of a Stretched String
Consider a string of length l , clamped rigidly at both ends A and B . When string is
plucked at P , identical wave travel along PA and PB , which are reflected at A and B .
The waves travelling in opposite direction will superimpose and produce standing wave.
The equation of these two waves are
y1 = 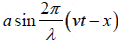 and y2 =
and y2 = 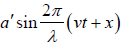
The equation of the resultant wave is y = 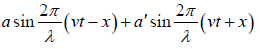
The two boundary conditions are (i) y = 0 at x = 0 and (ii) y = 0 at x = l
The first boundary condition gives a = −a′ , hence y = 
This represents a stationary wave.
The second boundary condition gives,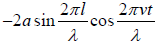 = 0
= 0
This must be true for all values of t, thus
 where n = 0,1,2,3....
where n = 0,1,2,3....
The allowed frequencies in such medium is f = 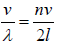
Since the velocity of transverse string is v = 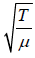
Thus the allowed frequency become f = 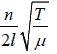
This shows that the string sustain vibration of certain discrete frequencies (n =1,2,3....) .
These frequencies are ‘Normal frequencies’ or ‘Normal Modes’ of the string.
The frequency corresponding to n =1 is called Fundamental Frequency of the string,
while those corresponding to n = 2,3,4.... are called first, second, third overtones. The
frequencies are in harmonic series (f1:f2:f3:......= 1:2:3...). Thus they are also called
Harmonics of the string.
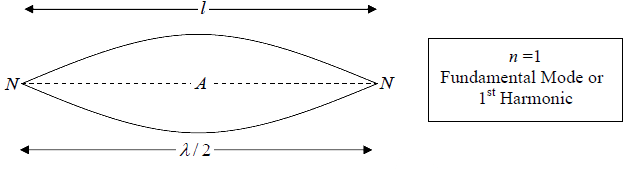
f1 = 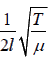 (Fundamental Mode or 1st Harmonic)
(Fundamental Mode or 1st Harmonic)
f2 = 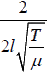 (1st overtone or 2nd Harmonic)
(1st overtone or 2nd Harmonic)
f3 = 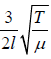 (2nd overtone or 3rd Harmonic)
(2nd overtone or 3rd Harmonic)
The allowed frequencies define the length of the string as an exact number of half
wavelengths.
l = 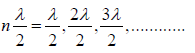
These modes are shown in the following figures:

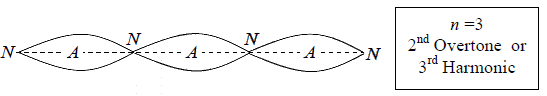
Example 5: A string 25cm long and having a mass of 2.5 g is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/ s find the tension in the string.
For a vibrating string, velocity of wave v =
μ =
When the string is set into its first overtone,
λ = 25cm = 25×10−2m = 0.25m
∴ Frequency = v/λ or f =
(i)
For pipe closed at one end,
Fundamental frequency = velocity/λ
f' = 320/ 4 x 0.4 = 200 Hz
Beat frequency = ( f − f ′) or ( f ′ − f )
∴ f depends upon tension T , ∴ f decreases when T , decreases
∴ Beat frequency (fb) decreases if fb = f − f ′ and (fb) increases if fb= f ′ − f .
According to condition given in question, fb decreases.
∴ fb = f − f ′⇒ 8 =
or 208 x 0.25 =
or 522 ×0.01 = T
⇒ T = 27.04N .
Phase Velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at
the phase velocity.
Consider a monochromatic wave with angular frequency ω = 2πν (where ν is the
frequency) travelling in +ve x -direction is given by
y = a sin (ωt − kx)
Consider a point on the sine wave at a particular instant of time the wave equation can be
written as y = asinωt.
After certain time say t0 if the point is displaced by a distance x the equation is given
by y= 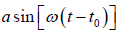
Velocity of the point v = x/t0 or t0 = x/v
Therefore y = 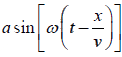 =
= 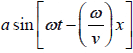 = a sin (ωt − kx) where k = ω/v
= a sin (ωt − kx) where k = ω/v
Where k is defined as the propagation constant or the wave number which is also
defined as k = 2π/λ. ‘ v ’ mentioned above as stated earlier is associated with the individual wave and hence it is nothing but phase velocity.
Thus phase velocity vp = ω/k
Group Velocity
A number of waves of different frequencies, wavelengths and velocities may be superposed to form a group. Waves rarely occur as single monochromatic components; a white light pulse consists of an infinitely fine spectrum of frequencies and the motion of such a pulse would be described by its group velocity. Such a group would, of course, ‘disperse’ with time because the wave velocity of each component would be different in all media except free space. Only in free space would it remain as white light. Its importance is that it is the velocity with which the energy in the wave group is transmitted. For a monochromatic wave the group velocity and the wave velocity are identical.
We begin by considering a group which consists of two components of equal amplitude
a but frequencies ω1 and ω2 which differ by a small amount.
Their separate displacements are given by y1 = a cos (ω1t − k1x) and y2 = a cos ω2t − k2x .
Superposition of amplitude and phase gives
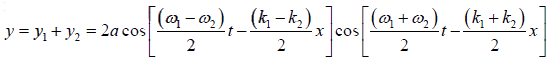
a wave system with a frequency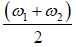 which is very close to the frequency of either
which is very close to the frequency of either
component but with a maximum amplitude of 2a , modulated in space and time by a very
slowly varying envelope of frequency 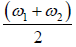 and wave number
and wave number 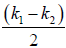 .
.
Then 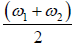 t -
t -  x = constant ⇒ vg =
x = constant ⇒ vg = 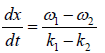
Figures shows that the faster oscillation occurs at the average frequency of the two
components 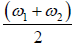 and the slowly varying group envelope has a frequency
and the slowly varying group envelope has a frequency , half the frequency difference between the components
, half the frequency difference between the components
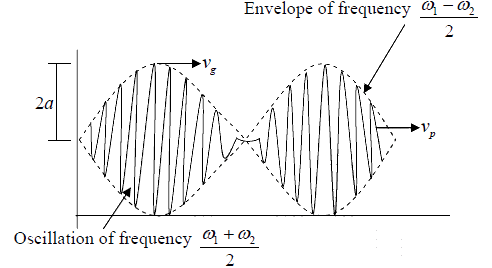
Wave Groups and Group Velocity
Suppose now that the two frequency components of the last section have different phase
velocities so that 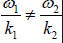 . The velocity of the maximum amplitude of the group; that is,
. The velocity of the maximum amplitude of the group; that is,
the group velocity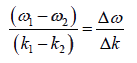
is now different from each of these velocities; the superposition of the two waves will no
longer remain constant and the group profile will change with time.
A medium in which the phase velocity is frequency dependent (ω/k not constant) is known as a dispersive medium and a dispersion relation expresses the variation of ω as a function of k . If a group contains a number of components of frequencies which are nearly equal the original expression for the group velocity is written
vg = 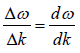
The group velocity is that of the maximum amplitude of the group so that it is the velocity with which the energy in the group is transmitted. Sinceω = kv , where v is the phase velocity, the group velocity
vg = 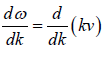 =
= 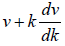 =
= 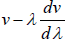 where k = 2π/λ .
where k = 2π/λ .
if dv/dλ is positive, then v > vg (Normal dispersion)
if dv/dλ is negative, then v < vg (Anomalous dispersion)
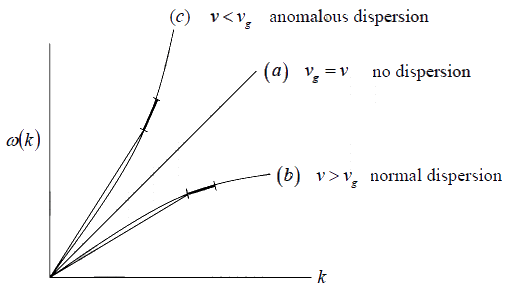
Above figure gives curves illustrating dispersion relations: (a) a straight line representing
a non-dispersive medium, v = vg ; (b) a normal dispersion relation where the gradient
v = 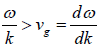 ; (c) an anomalous dispersion relation where v < vg .
; (c) an anomalous dispersion relation where v < vg .
The three curves of above Figure represent
- A non-dispersive medium where ω/k is constant, so that v = vg , for instance free
- space behaviour towards light waves.
- A normal dispersion relation v > vg .
- An anomalous dispersion relation v < vg .
Example 6: What are the values of phase velocity and group velocity respectively of the de-Broglie wave describing a free electron with velocity v?
According to de-Broglie, every moving object is associated with a wave,
known as de-Broglie wave. If m is mass of the object moving with velocity v then
associated wavelength λ is given as λ = h/mv where h is Planck’s constant
The velocity of wave front of constant phase is called phase velocity and is equal to the
velocity of the wave
Hence, phase velocity = λν , by energy equation mc2 = hv ⇒v = mc2/h
Thus Phase velocity = λ ×ν =
Now, the group velocity is given as vg = dω/dk
∵ ω =
and k
where m =
Thus, ω =
and k =
By differentiation we get,
dω/dv =
and dk/dv =
⇒ vg =
=
/
= v
|
365 videos|700 docs|149 tests
|
FAQs on Notes: Wave Motion - General Awareness - Bank Exams
| 1. What is the difference between a mechanical wave and an electromagnetic wave? |  |
| 2. How are wave fronts formed? |  |
| 3. What is the difference between traveling waves and stationary waves? |  |
| 4. How do longitudinal waves differ from transverse waves? |  |
| 5. What is the velocity of longitudinal waves? |  |