Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Number Operations
Number Operations | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Addition & Subtraction
What kind of addition or subtraction questions could I be asked?
- Adding and subtracting could be a part of any question within your GCSE course. Some examples include:
- Adding areas or volumes together in geometry questions
- Working with estimated mean or other averages
- Any problem-solving questions in a variety of contexts
- Simply showing that you have the skills to carry out these calculations without a calculator
- Different terms can be employed to indicate the action of including or deducting values.
- To indicate addition, one might use terms like "plus" or request to determine the total or sum.
- Conversely, for subtraction, alternatives such as "minus" or "take away" may be utilized, or one might be prompted to ascertain the difference.
- You must be confident with non-calculator methods for adding and subtracting large numbers and decimals.
How do I add large numbers?
- Arrange the numbers in a column format, ensuring that the ones, tens, hundreds, etc., are aligned vertically.
- For example, 382 + 943
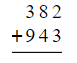
- For example, 382 + 943
- Begin by adding the numbers in each column, starting from the rightmost (units) column and progressing towards the left.
- Write each answer as a single digit below the line
- If the sum of a column results in a two-digit number, place the ones digit below the line and carry over the tens digit to the next column.
- For example, in the sum 382 + 943, the sum of the middle column is 12
- Put the 2 below the line and the 1 above the 3
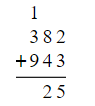
- Continue this process for all columns until every column has been added.
- If the sum of the leftmost (highest place value) column results in a two-digit number, write the entire number below the line as it represents the final answer.
- This is effectively the same as writing it at the top of the next column, but it would be the only number in that column
- For example when adding the 3 and 9 in the sum below
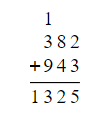
How do I subtract large numbers?
- This method involves writing one number above the other in a column, ensuring that all place values align.
- For instance, when subtracting 435 from 183:
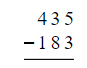
- Begin by subtracting the bottom number in each column from the top number in the same column, starting with the ones place.
- If a subtraction results in a negative number, "borrow" a ten from the column to the left.
- For example, when finding the difference between 435 and 183, if the difference between 3 and 8 is negative, borrow a ten from the hundreds column.
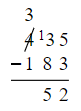
- This process is repeated for each subsequent column until the subtraction is complete.
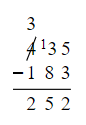
- Special cases:
- If borrowing is needed but the next column contains a zero, a ten can be borrowed from the column to the left.
- In 303 - 56, borrowing from the tens column involves transforming the zero into a ten for successful subtraction.
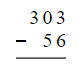
- Borrowing intricacies:
- In instances where the units column requires borrowing but can't borrow from the tens column, borrowing must begin from the hundreds column.
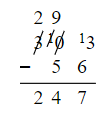
How to Add or Subtract with Decimals
- If the numbers involve decimals, ensure that the decimal points are aligned in a dedicated column.
- Keep the decimal point in the answer within this column as well.
- You might have to add zeros before or after the decimal point to maintain alignment.
- Estimate the answer by rounding to logical values to validate the correctness of your result.
Multiplication
Understanding Multiplication Questions
- Multiplication is a common element in GCSE questions, appearing in various scenarios such as:
- Finding areas or volumes in geometry problems
- Calculating distances based on speed and time
- Solving probability questions
- Tackling problem-solving challenges across different contexts
- Specific examples include:
- Determining areas or volumes in geometry tasks
- Calculating distances with known speeds and times
- Addressing probability scenarios
- Solving problems that require multiplication in various situations
- Vocabulary cues indicating multiplication include terms like "times," "multiply," or "product."
- Mastering non-calculator methods is crucial, particularly for handling large numbers and decimals without aid.
Strategies for Multiplying Numbers Without a Calculator
- The terms "times" or "multiply" might be used interchangeably, or you may be tasked to determine the product.
- Even though you have a calculator for calculations, you should be prepared to perform operations without it, especially in non-calculator exams. It's crucial to feel confident in multiplying large numbers and decimals.
- Being adept at demonstrating methods for multiplying large numbers and decimals is essential for success.
How to Multiply Multiple Numbers Manually?
- Various techniques suit different individuals, and effectiveness may vary based on the magnitude of the numbers involved. Below are three recommended methods depending on the scale of the numbers. Remember, all methods are applicable to all numbers!
- We suggest employing the following three approaches based on the scale of the numbers you are working with. When unsure, any of these methods can be used for any number.
1. Lattice Method:
- This technique is most effective for numbers containing two or more digits.
- It facilitates working with individual digits.
- For instance, in the number 3,516, you only need to focus on the digits 3, 5, 1, and 6.
- To multiply two numbers, one with two or more digits, place the longer number horizontally across the top of a grid and the shorter number to its right.
- Use diagonal lines to divide the tens and units in each part of the answer.
- Sum the digits by moving along the diagonals, starting from the right and proceeding leftward.
- If any diagonal totals a two-digit number, carry the tens value to the left and add it to the next section.
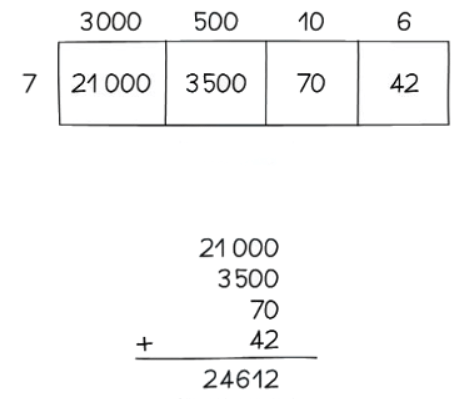
- For example, when multiplying 3,516 by 23, align the longer number horizontally and the shorter number vertically.
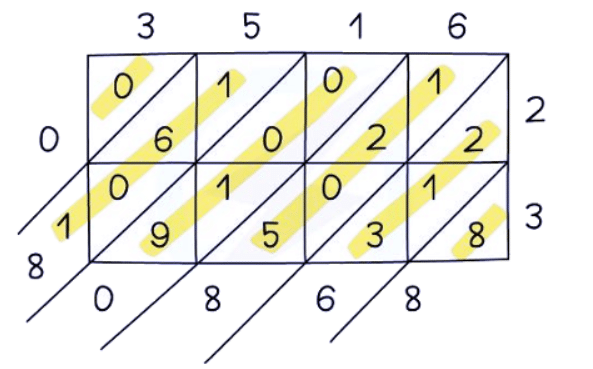 So, 3516 × 23 = 80 868
So, 3516 × 23 = 80 868
2. Partition Method:
- The partition method is beneficial for adding a large number with a one or two-digit number.
- It involves breaking down the larger number into its digit values. For example, for 3516, you would consider 3000, 500, 10, and 6.
- This method is not recommended for adding two larger numbers as it can lead to multiple zero digits that are challenging to manage.
3. Repeated addition method
- This method is ideal for smaller, less complex calculations.
- It is sometimes referred to as 'chunking'.
- The approach involves incrementally reaching the solution by utilizing basic multiplication facts that are easy to compute, for instance, calculating 13 x 23.
Using this method:- 1 x 23 = 23
- 2 x 23 = 46
- 4 x 23 = 92
- 8 x 23 = 184
- Therefore, 13 x 23 = 1 x 23 + 4 x 23 + 8 x 23 = 23 + 92 + 184 = 299
How do I multiply with decimals?
- When multiplying decimal numbers, there are three adaptable methods that can be used:
- You should ignore the decimal point during the multiplication process but remember to place it back in the correct position to obtain the final answer.
- For example, when calculating 1.3 x 2.3, without considering the decimals, it becomes 13 x 23, resulting in 299. Since there are two decimal places in the question, the answer should also have two decimal places. Therefore, 1.3 x 2.3 = 2.99.
- Always remember to estimate the approximate answer during exams to verify your calculations. For instance, 4.2 x 7.9 can be approximated to 4 x 8, which equals about 32.
Division
- Dividing two numbers could be a part of any question within your GCSE course, for instance:
- Converting a fraction to a decimal
- Finding the speed given a distance and a time
- Finding a length or a width given an area
- Problem-solving questions in various contexts
- When tackling division questions, you might encounter different terminologies indicating division:
- The words "divide," "quotient," "share," or "per" may appear
- You could be required to demonstrate a non-calculator method or perform a division without a calculator in exams.
- It's crucial to be adept at dividing both small and large numbers, as well as decimals.
How do I divide a number by another without a calculator?
- Short division, also known as the bus stop method, is preferred over long division.
- Short division is particularly effective when dividing by a single-digit number.
- However, when dividing larger numbers, alternative methods can be utilized.
- Other mathematical concepts such as cancelling fractions, employing shortcuts for dividing by 2 and 10, and applying the repeated addition method (chunking) from multiplication can be helpful.
- By leveraging these additional techniques, students can simplify the process of dividing larger numbers.
1. Short division (bus stop method)
- This method is most effective when dividing by a single digit, although shortcuts like dividing by 2 or 5 can also be utilized.
eg. 534 ÷ 6
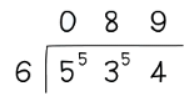
Therefore, 534 ÷ 6 = 89.
2. Factoring & Cancelling
- Division can be approached similar to cancelling fractions, especially in non-calculator scenarios where integer answers are common.
- It's crucial to note that for questions requiring a fraction to be written as a mixed number, different steps may be necessary.
- For instance, when dividing 1008 by 28, you can simplify it step by step: 1008 ÷ 28 = 504 ÷ 14 = 252 ÷ 7 = 36.
- For instance, consider dividing 1008 by 28. You can simplify this by breaking it down step by step: 1008 ÷ 28 = 504 ÷ 14 = 252 ÷ 7 = 36
- To do the last part (252 ÷ 7) you can use the short division method above
3. Dividing by Powers of 10
- Dividing by powers of 10 involves shifting digits in the place value columns.
- For example, 380 ÷ 10 = 38 and 45 ÷ 100 = 0.45. This showcases the process of moving digits according to the power of 10.
How do I divide a number by a decimal?
- When dividing by a decimal, convert it into an integer by multiplying by a power of 10.
- Both the dividend and divisor need to be adjusted for this calculation to simplify the process.
- Division can be simplified by converting problems into fractions. For instance, consider dividing 512 by 1.6.

- To tackle the example above, short division is the method of choice.
The document Number Operations | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|395 docs|19 tests
|
FAQs on Number Operations - Mathematics for GCSE/IGCSE - Class 10
| 1. How can I add large numbers efficiently? |  |
Ans. To add large numbers efficiently, it is helpful to break down the numbers into smaller, more manageable parts and add them sequentially. This can be done by aligning the numbers vertically and adding the digits in each place value column.
| 2. What is the process for subtracting large numbers? |  |
Ans. When subtracting large numbers, it is important to line up the numbers vertically and borrow from higher place values if necessary. Subtract each digit in the corresponding place value column and carry over any necessary borrowing.
| 3. How do I multiply large numbers? |  |
Ans. To multiply large numbers, use the long multiplication method by multiplying each digit of the second number by each digit of the first number, starting from the rightmost digit and carrying over any remainders.
| 4. What is the key to dividing large numbers? |  |
Ans. When dividing large numbers, use long division by dividing the dividend by the divisor, starting from the leftmost digit and working your way to the right. Keep track of the remainder and carry over to the next calculation if necessary.
| 5. How can I efficiently perform number operations in Year 11? |  |
Ans. To efficiently perform number operations in Year 11, it is important to practice and understand the basic mathematical concepts, such as addition, subtraction, multiplication, and division. Utilize different strategies and techniques to solve problems accurately and quickly.
Related Searches