Number Series Tips and Tricks for Government Exams
| Table of contents |

|
| Introduction |

|
| Common Patterns in Number Series |

|
| Tips to Solve Number Series Faster |

|
| Types of Number Series |

|
Introduction
Number series problems involve identifying the correct sequence of numbers, detecting mistakenly placed numbers, or finding missing numbers in a given series. Competitive exams test your ability to recognize patterns quickly and accurately.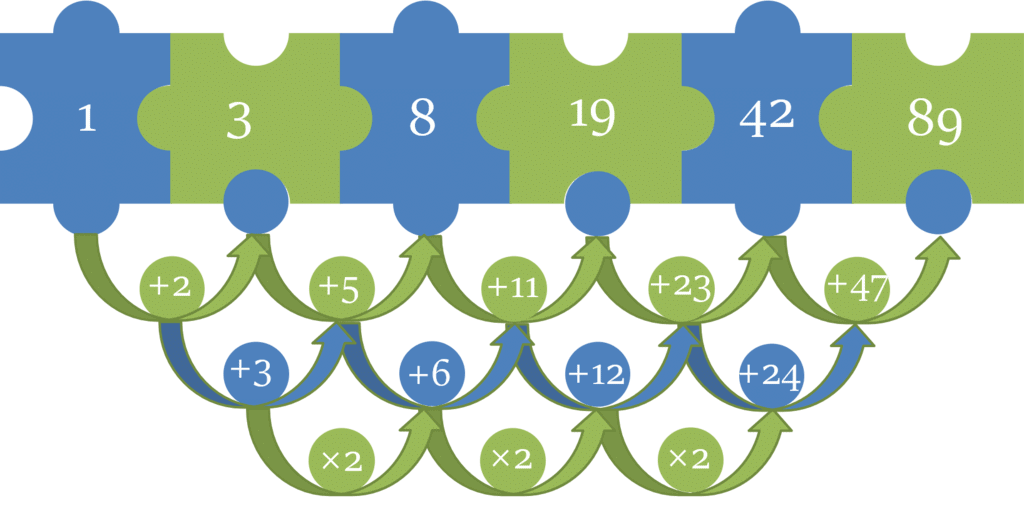
Common Patterns in Number Series
Arithmetic Series
Fixed difference between consecutive terms.
Example: 3, 7, 11, 15, ?
(Difference = +4 → Next term = 19)
Geometric Series
Fixed ratio (multiplication/division).
Example: 2, 6, 18, 54, ?
(Multiply by 3 → Next term = 162)
Square/Cube Series
Terms are squares or cubes of numbers.
Example (Squares): 1, 4, 9, 16, ?
(Next term = 25, since 5² = 25)Example (Cubes): 1, 8, 27, 64, ?
(Next term = 125, since 5³ = 125)
Prime Number Series
Sequence of prime numbers.
Example: 2, 3, 5, 7, ?
(Next term = 11)
Alternating Series
Two different operations alternate.
Example: 5, 10, 9, 18, 17, ?
(×2, -1, ×2, -1 → Next term = 34)
Fibonacci-Type Series
Sum of previous terms.
Example: 1, 1, 2, 3, 5, ?
(Next term = 8)
Tips to Solve Number Series Faster
✔ Check differences first, then ratios if needed.
✔ Look for squares, cubes, primes, or factorial patterns.
✔ Practice common series to improve speed.
✔ Break complex series into smaller parts.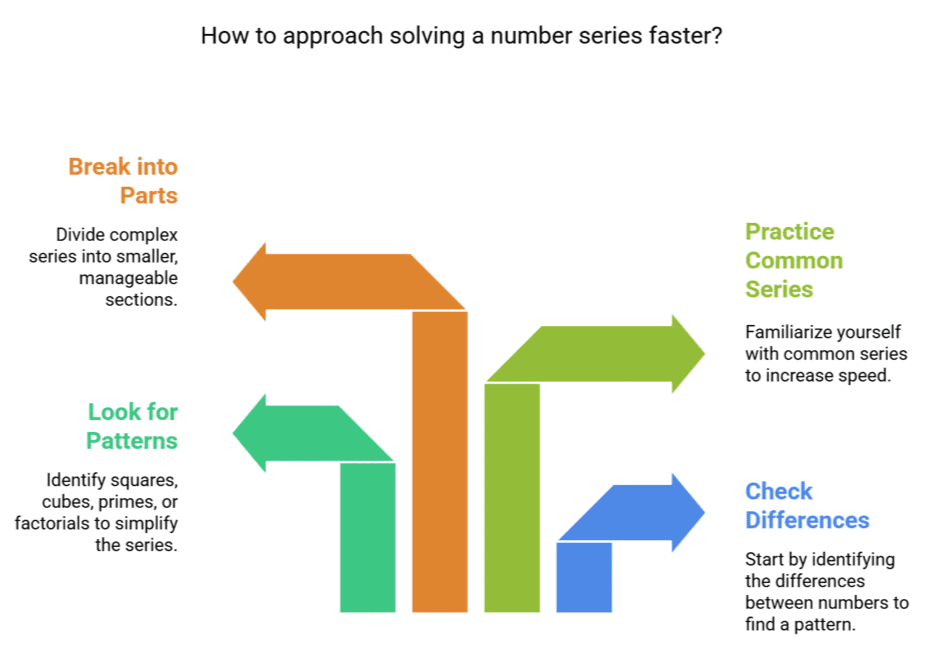
Types of Number Series
1. Perfect Square Series
Based on squares of numbers in order, with one missing.
Example: 1, 4, 9, 16, ?, 36
(Missing term = 25, since 5² = 25)
2. Perfect Cube Series
Based on cubes of numbers in order, with one missing.
Example: 1, 8, 27, ?, 125
(Missing term = 64, since 4³ = 64)
3. Geometric Series
Numbers obtained by multiplying/dividing by a fixed number.
Example: 3, 6, 12, 24, ?
(Multiply by 2 → Next term = 48)
4. Ratio Series
Numbers arranged based on a ratio pattern.
Example: 5, 10, 20, 40, ?
(Each term multiplied by 2 → Next term = 80)
5. Two-Stage Type Series
Differences between terms form another arithmetic series.
Example: 2, 5, 10, 17, 26, ?
(Differences: 3, 5, 7, 9 → Next difference = 11 → Next term = 26 + 11 = 37)
6. Mixed Series
Combination of different patterns arranged alternately.
Example: 2, 5, 10, 17, 26, ?
(Pattern: +3, +5, +7, +9 → Next term = 26 + 11 = 37)
Examples
6, 7, 12, 26, ?, 205.5
10 5 5 10 40 ?
96, 60, 35, ___, 10
|
67 videos|260 docs
|
FAQs on Number Series Tips and Tricks for Government Exams
| 1. What are number series? |  |
| 2. How to identify the pattern in a number series? |  |
| 3. How can I solve number series questions more efficiently? |  |
| 4. Are there any common tricks or shortcuts to solve number series questions? |  |
| 5. Can you provide an example of solving a number series question? |  |
















