Number Systems: Finding Remainders | Quantitative for GMAT PDF Download
In the GMAT, remainder problems involve understanding how to find the remainder when one number is divided by another.
These problems test your grasp of number properties, divisibility rules, and efficient calculation methods.

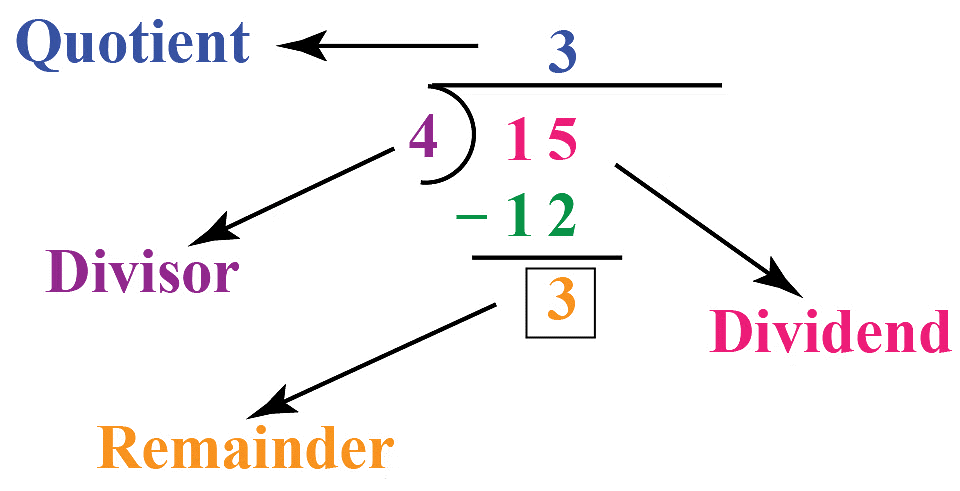
When a number A is divided by a number B, it can be represented in the form: A = B × Q + R
where,
- A is the dividend,
- B is the divisor
- Q is the quotient (the result of division), and
- R is the remainder, which must satisfy 0 ≤ R< B.
What is a Remainder?
- When you divide one number, called the "dividend," by another number, known as the "divisor," the result is expressed as a fraction, like "dividend/divisor."
- In a simple example, such as dividing 6 by 3 (6/3), the answer is 2, which is the "quotient"
- However, not all division problems are straightforward like 6/3; some result in "remainders" which is basically when a number does not divide the other number fully it leaves a number behind, which is called remainder.
- To put it simply, a remainder is the fractional part left over when you divide two numbers, and the division doesn't result in a whole number quotient.
- For example, when you divide 15 by 4 , the remainder is 3.
- Thinking of remainders as mixed numbers can be helpful. For instance, the fraction 8/3 is equivalent to the mixed number 2
 . Here, 2/3 represents the remainder, indicating that 2 parts are left out of the 3 parts needed to make a whole number. The denominator of the fraction will always be the same as the divisor.
. Here, 2/3 represents the remainder, indicating that 2 parts are left out of the 3 parts needed to make a whole number. The denominator of the fraction will always be the same as the divisor.
Finding Remainders of a Product (Derivative of Remainder Theorem)
(i) If ‘a1’ is divided by ‘n’, the remainder is ‘r1’ and if ‘a2’ is divided by ‘n’, the remainder is r2. Then,
(a) If a1+a2 is divided by n, the remainder will be r1 + r2.
(b) If a1 - a2 is divided by n, the remainder will be r1 - r2.
(c) If a1 × a2 is divided by n, the remainder will be r1 × r2.
Concept of Negative Remainder
- When you divide a negative number by a positive number, sometimes the remainder can be negative.
- But we usually need the remainder to be positive and between 0 and the divisor. So we adjust it to be positive.
For Example , Divide -8 by 5.
Sol:
Step 1: Perform the division of -8 by 5:-8 ÷ 5 gives a quotient of -2, and a remainder of -3. This can be written as:
-8 = 5 × (-2) + (-3)
Step 2: The remainder is negative (-3). To make the remainder positive, add 5 to -3:
-3 + 5 = 2
Step 3: Now the remainder is positive, and it is 2.
So, the remainder when -8 is divided by 5 is 2.
(ii) If two numbers ‘a1’ and ‘a2‘ are exactly divisible by n. Then their sum, difference and product is also exactly divisible by n.
i.e., If ‘a1’ and ‘a2’ are divisible by n, then
(a) a1 + a2 is also divisible by n
(b) a1 - a2 is also divisible by n
(c) a1 × a2 is also divisible by n.
For Example: 12 is divisible by 3 and 21 is also divisible by 3
Sol. So, Their sum will also be divisible by 3 i.e
12 + 21 = 33
Difference is also divisible by 3
12 - 21 = - 9 and
The product is also divisible by 3
12 × 21 = 252

Finding Remainders Of Powers With The Help Of Remainder Theorem
We will understand this concept using the following examples
Example 1: What is the remainder if 725 is divided by 6?
Solution: If 7 is divided by 6, the remainder is 1. So if 725 is divided by 6, the remainder is 1 (because 725 = 7 × 7 × 7… 25 times. So remainder = 1 × 1 × 1…. 25 times = 125).
Example 2: What is the remainder, if 363 is divided by 14.
Solution: If 33 is divided by 14, the remainder is - 1. So 363 can be written as (33)21.
So the remainder is (- 1)21 = - 1.
If the divisor is 14, the remainder - 1 means 13. (14 - 1 = 13) by pattern method.
Application Of Binomial Theorem In Finding Remainders
- The binomial expansion of any expression of the form
- (a + b)n = nCo an + nC1 an-1 × b1 + nC2 × an-2 × b2 ..... + nCn-1 × a1 × bn-1 + nCn × bn
- Where nCo, nC1, nC2, .... are all called the binomial coefficients
- In general, nCr = n!/r!(n - r)!
There are some fundamental conclusions that are helpful if remembered:
(a) There are (n + 1) terms.
(b) The first term of the expansion has only a.
(c) The last term of the expansion has only b.
(d) All the other (n - 1) terms contain both a and b.
(e) If (a + b)n is divided by a, then the remainder will be bn such that bn < a.
Example : What is the remainder if 725 is divided by 6?
- Sol: (7)25 can be written (6 + 1)25.
- So, in the binomial expansion, all the first 25 terms will have 6 in it.
- The 26th term is (1)25. Hence, the expansion can be written 6x + 1.
- 6x denotes the sum of all the first 25 terms.
- Since each of them is divisible by 6, their sum is also divisible by 6, and therefore, can be written 6x, where x is any natural number.
- So, 6x + 1 when divided by 6 leaves the remainder 1.
(OR)- When 7 divided by 6, the remainder is 1. So when 725 is divided by 6, the remainder will be 125 = 1.
Important Points
- The sum of consecutive five whole numbers is always divisible by 5.
- The square of any odd number when divided by 8 will leave 1 as the remainder
- The product of any three consecutive natural numbers is divisible by 6.
- The unit digit of the product of any nine consecutive numbers is always zero.
- For any natural number n, 10n-7 is divisible by 3.
- Any three-digit number having all the digits same will always be divisible by 37.
|
115 videos|106 docs|113 tests
|
FAQs on Number Systems: Finding Remainders - Quantitative for GMAT
| 1. What is a remainder in mathematics? |  |
| 2. How can the Remainder Theorem be used to find remainders of polynomial products? |  |
| 3. How can we find the remainder of powers using the Remainder Theorem? |  |
| 4. How does the Binomial Theorem apply in finding remainders? |  |
| 5. What are some important points to remember when finding remainders in number systems? |  |


 . Here, 2/3 represents the remainder, indicating that 2 parts are left out of the 3 parts needed to make a whole number. The denominator of the fraction will always be the same as the divisor.
. Here, 2/3 represents the remainder, indicating that 2 parts are left out of the 3 parts needed to make a whole number. The denominator of the fraction will always be the same as the divisor.

















