Best Study Material for Civil Engineering (CE) Exam
Civil Engineering (CE) Exam > Civil Engineering (CE) Notes > Engineering Mathematics > Numerical Methods
Numerical Methods | Engineering Mathematics - Civil Engineering (CE) PDF Download
Truncation errors and the taylor series
- Definition
Truncation errors are those that result from using an approximation in place of an exact mathematical procedure.
Example: Approximation of the derivative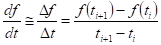
One of the most important methods used in numerical methods to approximate mathematical functions is: Taylor series. - Using taylor series to estimate truncation errors
Let us see how Taylor series may be used to estimate truncation errors.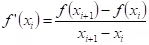
How to determine the error introduced by using this formulation to compute the derivative instead of using the real mathematical definition?
Using a Taylor series truncated at the first-order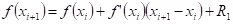
Therefore,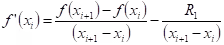
We have now an estimate of the truncation error:
Truncation error =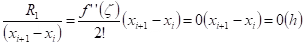
So the order of the error due to the formulation used to compute the derivative is h.
Numerical solution of ordinary differential equations (ODE)
- Definition
An equation that consists of derivatives is called a differential equation. Differential equations have applications in all areas of science and engineering. Mathematical formulation of most of the physical and engineering problems lead to differential equations. So, it is important for engineers and scientists to know how to set up differential equations and solve them. - Euler’s Method
Numerically approximate values for the solution of the initial-value problem 𝑦 ′ = 𝐹(𝑥, 𝑦), 𝑦 𝑥0 = 𝑦0, with step size ℎ, at 𝑥𝑛 = 𝑥𝑛 − 1 + ℎ, are
𝑦𝑛 = 𝑦𝑛 − 1 + ℎ ∙ 𝐹(𝑥𝑛 − 1, 𝑦𝑛 − 1)
Example: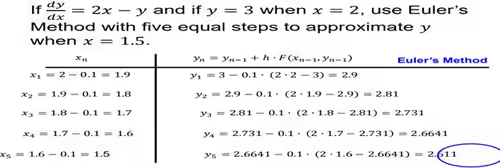
- Runge-Kutta 2nd order
The Runge-Kutta 2nd order method is a numerical technique used to solve an ordinary differential equation of the
dy / dx = f(x, y), y(0) = y0
Only first order ordinary differential equations can be solved by using the Runge-Kutta 2nd order method. In other sections, we will discuss how the Euler and Runge-Kutta methods are used to solve higher order ordinary differential equations or coupled (simultaneous) differential equations.
Example: Rewrite
dy / dx + 2y = 1.3e-x, y(0) = 5
in
dy / dx = f(x, y, y(0) = y0 form.
Solution: dy / dx + 2y = 1.3e-x, y(0) = 5
dy / dx = 1.3e-x -2y, y(0) = 5
In this case
f(x, y) = 1.3e-x - 2y
Numerical Integration
- Newton-Raphson Method
Let x0 be an initial guess to the root α of f(x) = 0. Let h is the correction i.e. α = x0 + h. Then f(α) = 0 implies f(x0 + h) = 0. Now assuming h small and f twice continuously differentiable, we find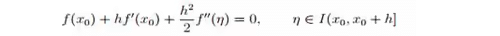
- Trapezoidal rule
Trapezoidal rule is based on the Newton-Cotes formula that if we approximate the integrand by an nth order polynomial, then the integral of the function is approximated by the integral of that nth order polynomial.
The trapezoidal rule works by approximating the region under the graph of the function f(x) as a trapezoid and calculating its area. It follows that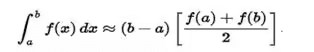
- Simpson’s 1/3rd Rule
Trapezoidal rule was based on approximating the integrand by a first order polynomial, and then integrating the polynomial in the interval of integration. Simpson’s 1/3rd rule is an extension of Trapezoidal rule where the integrand is approximated by a second order polynomial.
Since for Simpson’s 1/3rd Rule, the interval is broken into 2 segments, the segment width is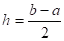
Hence the Simpson’s 1/3rd rule is given by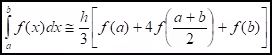
Since the above form has 1/3 in its formula, it is called Simpson’s 1/3rd Rule.
 |
Download the notes
Numerical Methods
|
Download as PDF |
Download as PDF
Roots of Equations
- False-Position Formula
A shortcoming of the bisection method is that in dividing the interval from xl to xu into equal halves, no account is taken of the magnitude of f(xi) and f(xu). Indeed, if f(xi) is close to zero, the root is more close to xl than x0.
The false position method uses this property:
A straight line joins f(xi) and f(xu). The intersection of this line with the x-axis represents an improved estimate of the root. This new root can be computed as: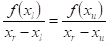
Giving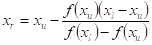 This is called the false-position formula
This is called the false-position formula - Secant method
Here we don’t insist on bracketing of roots. Given two initial guess. Given two approximation xn − 1, xn, we take the next approximation xn + 1 as the intersection of line joining (xn − 1, f(xn − 1)) and (xn, f(xn)) with the x-axis. Thus xn + 1 need not lie in the interval [xn − 1, xn]. If the root is α and α is a simple zero, then it can be proved that the method converges for initial guess in sufficiently small neighborhood of α.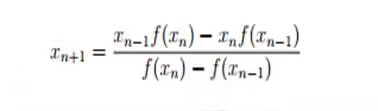
The document Numerical Methods | Engineering Mathematics - Civil Engineering (CE) is a part of the Civil Engineering (CE) Course Engineering Mathematics.
All you need of Civil Engineering (CE) at this link: Civil Engineering (CE)
|
65 videos|122 docs|94 tests
|
FAQs on Numerical Methods - Engineering Mathematics - Civil Engineering (CE)
| 1. What is Numerical Methods in the context of the GATE exam? |  |
| 2. What are some common topics covered under Numerical Methods in the GATE exam? |  |
Some common topics covered under Numerical Methods in the GATE exam include numerical solutions of linear and nonlinear equations, interpolation and approximation, numerical differentiation and integration, numerical methods for solving ordinary differential equations, numerical optimization, and numerical linear algebra.
| 3. How can I prepare effectively for the Numerical Methods section in the GATE exam? |  |
To prepare effectively for the Numerical Methods section in the GATE exam, you can start by understanding the fundamental concepts and algorithms related to the different topics mentioned earlier. It is important to practice solving numerical problems and implementing algorithms using programming languages like MATLAB or Python. Referring to standard textbooks and solving previous years' GATE question papers can also be helpful in gaining a better understanding of the subject.
| 4. Are there any specific tips or strategies to improve performance in the Numerical Methods section of the GATE exam? |  |
Yes, here are some tips to improve performance in the Numerical Methods section of the GATE exam:
- Practice solving numerical problems regularly to improve your speed and accuracy.
- Understand the underlying algorithms and their applications in different contexts.
- Focus on understanding the concepts and their derivations rather than memorizing formulas.
- Solve previous years' GATE question papers to get familiar with the exam pattern and identify important topics to prioritize.
- Use online resources, video tutorials, and online forums to clarify doubts and gain additional insights into the subject.
| 5. Can you suggest some reference books for studying Numerical Methods for the GATE exam? |  |
Yes, here are some popular reference books for studying Numerical Methods for the GATE exam:
- "Numerical Methods: Principles, Analysis, and Algorithms" by G. Shanker Rao
- "Numerical Methods for Engineers" by Steven C. Chapra and Raymond P. Canale
- "Numerical Methods: A MATLAB Approach" by Abdelwahab Kharab and Ronald B. Guenther
- "Numerical Methods: Using MATLAB" by George Lindfield and John Penny
- "An Introduction to Numerical Methods: A MATLAB Approach" by Abdelwahab Kharab and Ronald B. Guenther
These books provide a comprehensive understanding of the subject and include examples, practice problems, and MATLAB programming exercises to enhance your learning experience.
Related Searches




















