Olympiad Notes: Patterns in Mathematics | Maths Olympiad Class 6 PDF Download
| Table of contents |

|
| Patterns in Mathematics |

|
| What is Mathematics? |

|
| Types of Patterns in Maths |

|
| Visualizing Number Sequences |

|
Patterns in Mathematics
Mathematics extends beyond mere numbers and equations; it is an engaging journey to uncover and comprehend the patterns that exist in different forms around us. This chapter explores these patterns in-depth, illuminating the essence of mathematics and its wide-ranging applications.
What is Mathematics?
Mathematics is often described as a search for patterns and the explanations behind them.
These patterns are not limited to abstract numbers; they are all around us—ranging from natural phenomena to daily activities. Whether it’s the arrangement of objects in our homes, the cycles of celestial bodies, or the structures in technology, patterns are everywhere.
Types of Patterns in Maths
Let’s look at the different types of patterns in maths, along with examples to make them easy to understand.
Ascending Patterns
An ascending pattern is when the numbers get bigger each time. This usually happens through addition or multiplication.
For example, in the sequence 5, 10, 15, 20, 25, we can see that each number is five more than the one before. That means the rule for this pattern is to add five every time.
Another example is 3, 6, 12, 24, 48. Here, each number is twice the previous one. So, the rule is to multiply by two each time.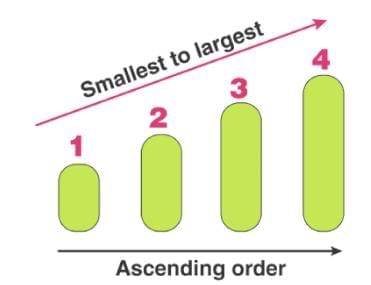
Descending Patterns
A descending pattern is when the numbers get smaller each time. This often involves subtraction or division.
Take the pattern 50, 45, 40, 35, 30. Each number is five less than the one before. The rule here is to subtract five every time.
In the pattern 81, 27, 9, 3, each number is one-third of the previous one. The rule here is to divide by three at each step. 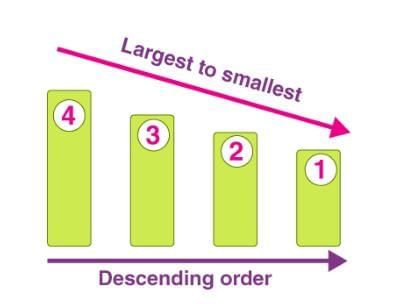
Repeating Patterns
Repeating patterns are patterns where a certain group of elements appears over and over in the same order. These can be numbers, shapes, colours, or letters.
Example: Pink, White, Blue, Pink, White, Blue,...
This kind of pattern is commonly seen in designs like borders, wallpapers, and floor tiles. You can extend it simply by repeating the group again.
 Repeating Pattern
Repeating Pattern
Letter Patterns
These patterns use alphabets arranged in a meaningful sequence. They often follow alphabetical order or a set rule.
Example: A, C, E, G, I...
In this sequence, each letter skips the next one in the alphabet. Letter patterns are useful in puzzles, code-breaking, and language-based reasoning. Letter Pattern
Letter Pattern
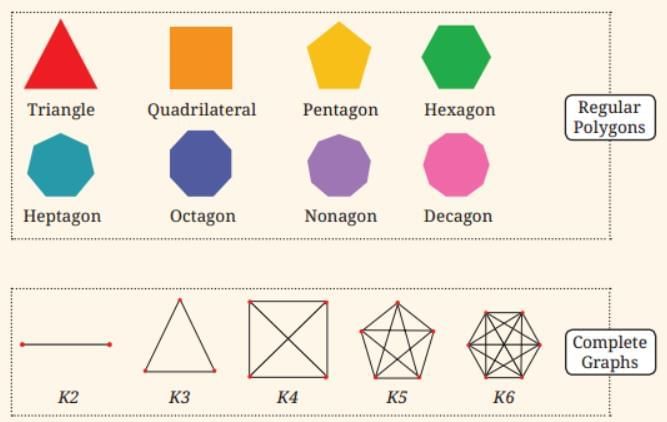
Shape Patterns
Mathematics also explores patterns in shapes, which can be in one, two, or three dimensions. This field, known as geometry, studies various shape sequences:
- Stacked Triangles
- Complete Graphs: K₂, K₃, K₄, K₅, K₆
- Stacked Squares
- Koch Snowflake
- Regular Polygons: Triangle, Pentagon, Hexagon, etc.


Number Patterns
One of the most fundamental aspects of mathematics is the study of patterns in numbers. This branch of mathematics, known as number theory, explores various sequences and patterns within whole numbers. Here are some essential number sequences you will encounter: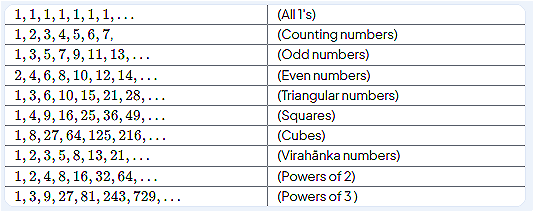
These sequences are not just numbers; they represent different patterns and structures that can help us understand more complex mathematical concepts.
Relations Among Number Sequences
Number sequences can often be related in intriguing ways. For example, when you sum odd numbers sequentially:
- 1=1
- 1 + 3 = 4
- 1 + 3 + 5 = 9
- 1 + 3 + 5 + 7 = 16
- 1 + 3 + 5 + 7 + 9 = 25
- 1 + 3 + 5 + 7 + 9 + 11 = 36
You discover that these sums produce square numbers. This pattern is not only beautiful but also demonstrates how understanding one sequence can reveal insights into another.
Visualizing Number Sequences
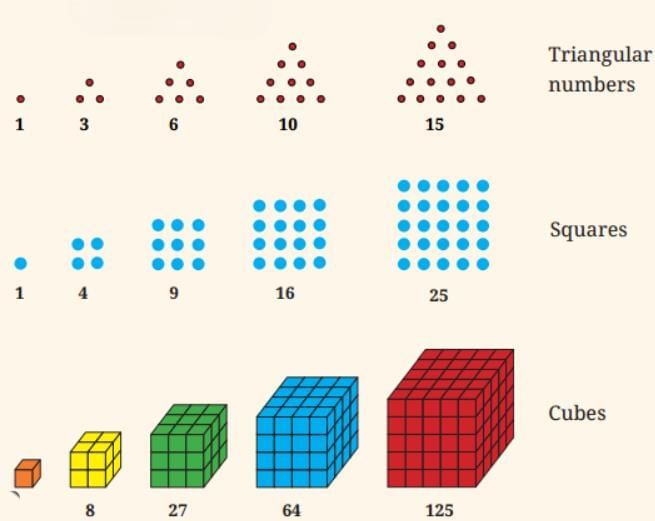
Visualization is a powerful tool in mathematics. By representing number sequences with pictures or diagrams, you can gain a clearer understanding of the patterns. For instance:
- Squares: Visualize square numbers by arranging dots in a square grid.
- Triangular Numbers: Picture these as triangular arrangements of dots.
- Cubes: Imagine these numbers as stacked cubes.
These visual representations help illustrate why certain patterns exist and can make abstract concepts more tangible.
|
33 videos|126 docs|55 tests
|
FAQs on Olympiad Notes: Patterns in Mathematics - Maths Olympiad Class 6
| 1. What are the main types of patterns in mathematics? |  |
| 2. How can visualizing number sequences help in understanding patterns? |  |
| 3. What is the significance of studying patterns in mathematics for Class 6 students? |  |
| 4. Can you provide examples of numerical patterns that are commonly encountered? |  |
| 5. How do Olympiad competitions incorporate patterns in mathematics? |  |




















