Operation on Real Numbers | Advance Learner Course: Mathematics (Maths) Class 8 PDF Download
| Table of contents |

|
| Real Numbers |

|
| Operation on a rational number and an irrational number |

|
| Properties of Real Numbers |

|
| Rationalization |

|
Real Numbers
 Real Number Operations
Real Number Operations
Real numbers are those numbers that are a combination of rational numbers and irrational numbers in the number system of maths. All the arithmetic operations like addition, subtraction, multiplication, etc. can be performed on these numbers. Besides imaginary numbers are not real numbers. Imaginary numbers are used for defining complex numbers. To get real numbers, first, we have to understand rational numbers and irrational numbers. Rational numbers are those numbers that can be written as p/q where p is numerator and q is dominator and p and q are integers. For example, 5 can be written as 5/1 so it is a rational number and irrational numbers are those numbers that cannot be written in form of p/q.
For example √3 is irrational numbers, it can be written as 1.73205081 and continuous to infinity, and it cannot be written in form of fraction and is non-terminating form and non-recurring decimals. And if combine rational numbers and irrational numbers it became real numbers.
Example: 12, -8, 5.60, 5/1, π(3.14) etc.
Real numbers can be positive and negative, and it is denoted by R. All the decimals, natural numbers and fraction come under this category.
Operations on Real Numbers
The four basics mathematical operations addition, division, multiplication, and subtraction. Now we will understand these operations on both rational and irrational numbers.
Operation on Two Rational Numbers
When we perform arithmetic operations on two rational numbers like addition, subtraction, division, and multiplication then the result will be rational numbers.
Example:
- 0.25 + 0.25 = 0.50 can be written as 50/100 which is form of p/q.
- 0.20 – 0.10 = 0.10 can be written as 10/100 which is form of p/q.
- 0.4 multiplied by 184 is 73.6 and can be written as 736/10.
- 0.252 divided by 0.4 is 0.63 and can be written as 63/100.
Operations on Two Irrational Numbers
When we perform arithmetic operations like addition, subtraction, multiplication, or division on two irrational numbers then the result can be rational numbers or irrational numbers.
Example:
- √2 + √3 = 3.14 can be written as 314/100 which is rational number.
- √3 – √3 = 0 or 5√4 – 4√3 = 3.07 which can be written as 307/100 which is rational number.
- When √5 is multiplied to √5, we get 5 which is rational number or when √3 is multiplied to √5, we get √15 which is irrational number. When √8 is divided by √8 we get 8 which is rational number or if √5 is divided by √3 then we get (√5)/(√3) which is irrational number.
Operation on a rational number and an irrational number
 Irrational Number Operations
Irrational Number Operations
Addition
- When we add an irrational number and a rational number then the result will be an irrational number. When 3 is added to 2√5 then the result will be an irrational number.
Subtraction
- When we perform subtraction on an irrational number and a rational number then the result will be an irrational number. When 5√6 is subtracted to 3 then the result will be an irrational number.
Multiplication
- When we perform this operation the result can be irrational or rational. When 3 is multiplied to √5 then the result will be 3√5 which is an irrational number and if √12 is multiplied to √3 then the result will be √36 and it can be written as 6 which is a rational number.
Division
- A rational number is divided by an irrational number or vice versa then the result will be always an irrational number. When 4 is divided by √2 then results will be 4√2 which is an irrational number.
Properties of Real Numbers
 Real Numbers Properties
Real Numbers Properties
We have four properties which are commutative property, associative property, distributive property, and identity property. Consider a, b and c are three real numbers. Then these properties can be described as
Commutative Property
- If a and b are the numbers, then a + b = b + a for addition and a × b = b × a for multiplication.
Addition
- a + b = b + a;
- 5 + 6 = 6 + 5
Multiplication
- a × b = b × a;
- 4 × 2 = 2 × 4
Associative Property
- If a, b and c are the real numbers then the form will be
- a + (b + c) = (a + b) = c for addition and (a.b)c = a(b.c) for multiplication
Addition
- a + (b + c) = (a + b) = c ;
- 5 + (3 + 2) = (5 + 3) + 2
Multiplication
- (a.b)c = a(b.c) ;
- (4 × 2) × 6 = 4 × (2 × 6)
Distributive Property
- If a, b and c are the real numbers then the final form will be
- a (b + c) = ab + ac and (a + b) c = ac + ab
- 5 (2 + 3) = 5 × 2 + 5 × 3 the answer will be 25 for both left and right term.
Identity Property
- Addition: a + 0 = 0 (0 is the additive identity)
- Multiplication: a × 1 = 1 × a = 1 (1 is multiplicative identity)
Real Numbers
- Rational numbers: 4/5, 0.82
- Integer numbers: {… – 3, -2, -1,0,1,2,3…}
- Whole numbers: {0,1,2,3…}
- Natural numbers: {1,2,3…}
- Irrational numbers: √2, π, 0.102012…
Sample Problems
Question 1. Show that 3√7 is an irrational number.
Solution:
Let us assume, to the contrary, that 7√7 is rational.
That is, we can find coprime a and b (b ≠ 0) such that 7√7 = ab
Rearranging, we get √7 = ab/7
Since 7, a and b are integers, ab/7 is rational, and so √7 is rational.
But this contradicts the fact that √7 is irrational.
So, we conclude that 7√7 is irrational.
Question 2. Explain why (17 × 5 × 13 × 3 × 7 + 7 × 13) is a composite number?
Solution:
17 × 5 × 13 × 3 × 7 + 7 × 13 …(i)
= 7 × 13 × (17 × 5 × 3 + 1)
= 7 × 13 × (255 + 1)
= 7 × 13 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore, (17 × 5 × 13 × 3 × 7 + 7 × 13) is a composite number.
Question 3. Prove that 3 + 2√3 is an irrational number.
Solution:
Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = ab, where a and b are coprime.
Rearranging the equations, we get since a and b are integers, we get a2b−32 is rational and so √3 is rational.
But this contradicts the fact that √3 is irrational.
So we conclude that 3 + 2√3 is irrational.
Rationalization
Rationalization is a process that finds application in elementary algebra, where it is used to eliminate the irrational number in the denominator. There are many rationalizing techniques which are used to rationalize the denominator. The word rationalize literally means making something more efficient. Its adoption in mathematics means making the equation reduced into its more effective and simpler form.
Rationalization can be considered as the process used to eliminate a radical or an imaginary number from the denominator of an algebraic fraction. That is, remove the radicals in a fraction so that the denominator only contains a rational number. Let us recall some important terms relating to the concept of rationalization in this section.
Radical
A radical is an expression that uses a root, such as a square root, cube root. For example, an expression of the form: √(a + b) is radical.
Radicand
Radicand is the term we are finding the root of. For example, In the following figure, (a + b) is the radicand.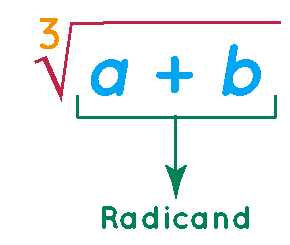
Radical Symbol
The √ symbol means "root of". The length of the horizontal bar is important. The length of the bar signifies variables or constants that are a part of the root function. The variables or constants that are not under the root symbol are hence not part of the root.
Degree
The degree is the number depicted in the figure below. 2 means square root, 3 means cube root. Further, they are referred to as 4th root, 5th root, and so on. If this is not mentioned, we take it as square root by default.

Conjugate
A math conjugate of any binomial means another exact binomial with the opposite sign between its two terms. For example, the conjugate of (x + y) is (x - y) or vice versa. Thus, both these binomials are conjugates of each other.
Rationalizing a Surd
Surds are irrational numbers that cannot be further simplified in their radical form. For example, an irrational number √8 can be simplified further as 2√2, whereas √2 cannot be simplified any further. Thus √2 is a surd.
Examples of a monomial radical: √6, 3√2, 3 √ 2
Examples of a binomial radical: √3 + √6, 1 - √2
The procedure to rationalize an expression depends on the radical if that is monomial or binomial.
Rationalizing a Monomial Radical
To rationalize a surd or radical, in the denominator, different steps are to be followed depending upon the degree of the polynomial or the fact that if the radical is a monomial or polynomial. Any polynomial with only one term is called a monomial. √ 2, √ 7x, 3√7x, etc. could be in the denominators.
Procedure:
1) Suppose the denominator contains a radical, as in this fraction:a/√ b. Here, the radical must be multiplied and divided by √ b and further simplified.
2) For a polynomial with a monomial radical in the denominator, say of the form, a m √ x n , such that n < m, the fraction must be multiplied by a quotient containing a m √ x ( m − n ) , both in the numerator and denominator. This gives us the result a m √ x m , which can be replaced by x and hence free of the radical term.
|
5 videos|57 docs|20 tests
|
FAQs on Operation on Real Numbers - Advance Learner Course: Mathematics (Maths) Class 8
| 1. What is a rationalization operation on real numbers? |  |
| 2. Why would someone perform a rationalization operation on real numbers? |  |
| 3. How do you rationalize the denominator of a fraction? |  |
| 4. Can you provide an example of rationalizing the denominator? |  |
| 5. Are there any cases where rationalization is not necessary or recommended? |  |















