Origin of Energy Bands | Solid State Physics, Devices & Electronics PDF Download
Origin of Energy Bands
The failure of the free electron model is due to the over simplified assumption that a conduction electron in a metal experiences a constant or zero potential due to the ion cores and hence is free to move about crystal.
Now the periodic potential described below forms the basis of the band Theory of solids. The behavior of an electron in this potential is describe by constructing the electron wave functions using one-electron approximates.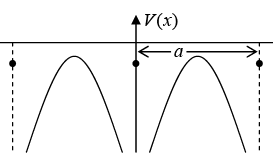
As we shall discuss later, the motion of an electron in a periodic potential yields the following results.
(a) There exist allowed energy bands separated by forbidden region or band gap.
(b) The electronic energy function E(K) is periodic in the wave vector K
In the free electron Theory E varies with K
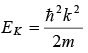
The Block Theorem
The 1-D Schrödinger equation for an electron moving in a constant potential V0 is  The solution ψ(x) = e±ikx
The solution ψ(x) = e±ikx
For periodic potential with period equal to the lattice constant a we have
ψ(x) = e±ikx Uk(x) where Uk = Uk (x + a)
Note: Let g(x) and f(x) be two real and independent solution to the second order differential The general equation can be written as ψ(x) = A f(x) + B g(x)
while 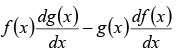 = constant
= constant
In three dimensions, the block Theorem is expressed as 
Thus the wave function becomes the one of a free electron.
The Kronig-Penney Model
This model illustrates the behaviour of electrons in a periodic potential by assuming a relatively simple one-dimensional model of periodic potential as shown figure.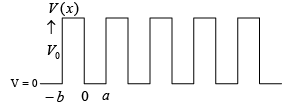
For this potential write down the Schrödinger wave equation and its general solution with taking potential constant finally. We get
which is a measure of the area V0b of the potential barrier. Thus increasing P has the physical meaning of bonding an electron more strongly to a particular potential well
We know that 
It may be noted that since α2 is proportional to the energy E the abscissa is a measure of the energy. The following conclusion may be drawn from figure.
(i) The energy spectrum of the electrons consists of alternate regions of allowed energy bands (solid lines on abscissa) and forbidden energy band (broken lines)
(ii) The width of the allowed energy bands increases with αa or the energy
(iii) The width of particular allowed energy band decreases with increase in value of P.
Figure- Allowed (shaded) and forbidden (open) energy ranges as a function of P
Energy Verses Wave-Vector relationship
The energy E is also an even periodic function of k with period of 2π/a i.e k = ± nπ/a
dn = (1/2π)dk
Velocity is 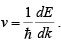
Concept Effective Mass and Holes
In one dimension, an electron with wave-vector k has group velocity 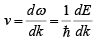 ...(i)
...(i)
If an electric field ε acts on the electron, then in time δ t . It will do work
δ E = force times distance= −eε vδ t (ii)
But 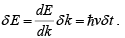 (iii)
(iii)
So, comparing equation (ii) with (iii), we have
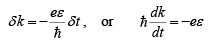 (iv)
(iv)
In terms of force F, 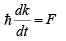
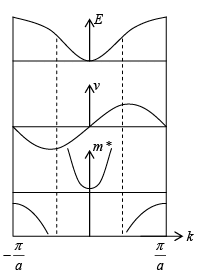
Generalising to three dimensions: 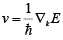
where 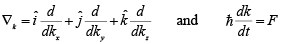
From equation (i) v 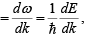
Differentiating with respect to time 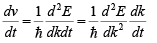
But from equation (iv), 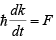
So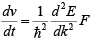
But from Newton’s equation we expect 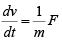
which leads us to define an effective mass 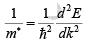
That is
The dynamics of electrons is modified by the crystal potential;
The effective mass depends on the curvature of the bands;
Flat bands have large effective ma
Near the bottom of a band, m* is positive, near the top of a band, m* is negative.
Hole Concept
➤ Hole wavevector: The total k of a full band is zero: if we remove an electron with wavevector ke the total k of the band is kh +ke = 0⇒ kh = −ke
➤ Hole energy: Take the energy zero to be the top of the valence band. The lower the electron energy, the more energy it takes to remove it; thus
Eh(kh) = -Ee(ke)
But bands are usually symmetric, E(k) =E (−k)
So Eh(kh) = Eh(-kh) = -Ee(ke)
➤ Hole velocity: In three dimensions 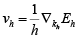
But kh =−ke So 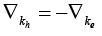
and so 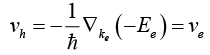
The group velocity of the hole is the same as that of the electron.
➤ Hole effective mass: The curvature of E is just the negative of the curvature of − E ,
So mh* = −me*
Note that this has the pleasant effect that if the electron effective mass is negative, as it is at the top of the band, the equivalent hole has a positive effective mass.
➤ Hole dynamics
We know that 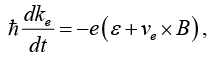
Substituting kh =−ke and vh = ve gives 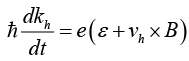
Exactly the equation of motion for a particle of positive charge.
Under an electric field, electrons and holes acquire drift velocities in opposite directions, but both give electric current in the direction of the field.
|
91 videos|21 docs|25 tests
|
FAQs on Origin of Energy Bands - Solid State Physics, Devices & Electronics
| 1. What is the origin of energy bands in materials? |  |
| 2. How do energy bands determine the electrical properties of materials? |  |
| 3. What is the significance of energy band structure in semiconductors? |  |
| 4. How are energy bands experimentally studied in materials? |  |
| 5. Can the energy band structure of a material be modified? |  |
















