Orthotropic Hooke’s Law - Civil Engineering (CE) PDF Download

Orthotropic Hooke’s law
From the above exposition it would have been clear that isotropic Hooke’s law is an approximation to a more general theory. We could proceed in a similar fashion to obtain orthotropic Hooke’s law. On the other hand, as is done in many textbooks on linearized elasticity, we can begin by stating that the Cauchy stress is linearly related to the linearized strain, impose the restriction due to material symmetry on this constitutive relation and obtain isotropic or orthotropic Hooke’s law. However, there are some differences in the orthotropic Hooke’s law obtained by these two approaches. Without develing into these differences, in this section we obtain the orthotropic Hooke’s law by the second approach.
Since, we assume that the second order tensor stress is linearly related to another second order tensor, the strain, we say that the stress is obtained by the action of a fourth order tensor on strain,

σ = C : ∈,                                   (6.120)

where C is the fourth order elasticity tensor. Equivalently, one may invert the equation (6.120) to write strain in terms of stress as,

∈ = D : σ,                                   (6.121)

where D is the fourth order elastic compliance tensor.

Recalling from chapter 2 (section 2.4) the fourth order tensor has 81 components. As discussed in section 2.4.1, for the following discussion it is easy to view second order tensors as column vectors with 9 components and fourth order tensors as 9 by 9 matrix. By virtue of the stress and strain being symmetric tensors, with only six independent components equation (6.120)
can be written as,



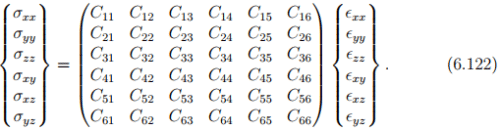
Thus, of the 81 components only 36 are independent.
As stated before, since elastic process is non-dissipative, the stress is derivable from a potential called the stored (or strain) energy, W as,
 

                             (6.123)

where W =Ŵ (∈). The above equation in index notation is given by

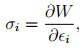                                 (6.124)

when the stress and strain tensors are represented as column vectors with six components. Now, σ₁ = σ_xx, σ₂ = σ_yy, σ₃ = σ_zz, σ₄ = σ_xy, σ₅ = σ_xz, σ₆ = σ_yz and ∈₁ = ∈_xx, ∈₂ = ∈_yy, ∈₃ = ∈_zz, ∈₄ = ∈_xy, ∈₅ = ∈_xz, ∈₆ = ∈_yz. This is just a change in notation. It follows from (6.120) that the elasticity tensor could be obtained from

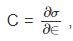  in index notation  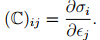                   (6.125)

Substituting (6.124) in the above equation,

                         (6.126)

Thus, if W is a smooth function of strain, which it is, then the order of differentiation would not matter. Hence, elasticity tensor would be a symmetric fourth order tensor. This means that the number of independent components in C reduces from 36 to 21 components.

Further reduction in the number of independent components of the elasticity tensor cannot be done by restriction due to non-uniqueness of placers argument. Given that, due to equivalent placement of the body the displacement gradient transforms as given in equation (6.19) and Cauchy stress transforms as given in equation (6.25), it is evident that the restriction due to non-uniqueness of placers is not met by the constitutive relation (6.120). Then, due to changes in the coordinate basis, the elasticity tensor should transforms as
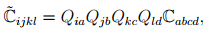             (6.127)

according to the transformation law for fourth order tensor (see section 2.6). Ideally we should require that the components of the elasticity tensor be the same irrespective of the choice of the basis. In other words, this means, as discussed in section 2.6.3, that the elasticity tensor should be the isotropic fourth order tensor. Since, the elasticity fourth order tensor is symmetric, in the general representation for the isotropic fourth order tensor (2.165), γ = β = � and thus,
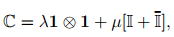                          (6.128)

where we have replaced the constant α with λ. This λ and � are the same Lam`e constants. Writing (6.128) in matrix form,

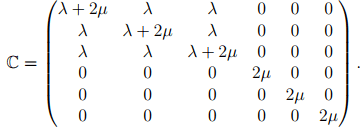                      (6.129)

Thus, we have obtained the isotropic form of the Hooke’s law.

Contrary to this ideal requirement, it is required that the components of the elasticity tensor be the same only for certain equivalent choices of the basis vectors. A material with three mutually perpendicular planes of symmetry is called orthotropic. This means that 180 degree rotation about each of the coordinate basis should not change the components of the elasticity tensor. Thus, for an orthotropic material the components of 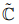 must be same as that of C in (6.127) for the following choices of



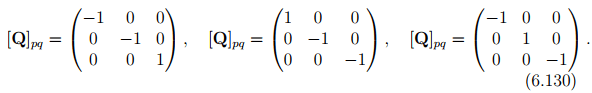
It can be seen that as a result of this condition, the number of independent components in the elasticity tensor reduces from 21 to 9 for an orthotropic material and hence C for an orthotropic material is given by:

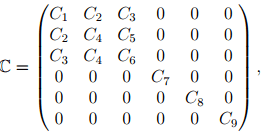                        (6.131)

where C₁, C₂, . . ., C₉ are material parameters. Similarly, for other equivalent choices of the basis vector, we obtain different forms for the elasticity tensor.

One can now define material parameters like Young’s modulus, Poisson’s ratio, shear modulus and elaborate on the experiments that needs to be done to estimate the 9 constants characterizing the orthotropic material. Then, one can look at restrictions on them. Instead of doing these, we now focus on solving boundary value problems involving isotropic materials that obey Hooke’s law.