Overview: Quantitative Reasoning | General Intelligence and Reasoning for SSC CGL PDF Download
What is Quantitative Reasoning?
- Quantitative Reasoning is the ability to understand and solve mathematical problems using basic arithmetic operations such as addition, subtraction, multiplication, and division.
- Quantitative reasoning questions are common in all kinds of aptitude exams and require the student to work out numerical relationships as defined by the parameters in the problem.
- Quantitative reasoning is not only about the ability to perform calculations but also about understanding the underlying concepts, recognizing patterns, and making informed decisions based on numerical data.

- Arithmetic Reasoning tests the mathematical knowledge of a candidate. Questions that are based on arithmetic reasoning are usually numerical in nature, so they contain calculation parts in many cases. Candidates who don’t like mathematics will find the arithmetic reasoning section unfavourable for them, but with clear concepts and practice they can easily ace this section.
- Example:
The classic quantitative reasoning question:A man would like to take a new health insurance. An officer taking care of these matters says to the man,"Pleasetell me how many children you have." The man answers,"I have three of them." The officer,"What are the agesof your children?" The man answers, "The product of the ages is equal to 36." The officer replies, "This is not enough information, Sir!"; the man replied, "Sorry that I was a little bit unclear, but the sum of the ages is equal to the number of shops in front of your office." The of-ficer: "This still isn't enough information, Sir!"; The man replies,"My oldest child loves chocolate." The officer: "Thanks for your cooperation, I now know the ages." Are you as smart as the officer? Then, give the sum of the ages of the children.
1. 13
2. 22
3. 36
4.38
Solution: The product of the ages is 36*. Using this, one can make the following combination of ages:1, 36, 1 sum = 381, 18, 2 sum = 211, 12, 3 sum = 161, 9, 4 sum = 141, 6, 6 sum = 132, 9, 2 sum = 132, 6, 3 sum = 113, 3, 4 sum = 10After the man had said that the product of the ages is equal to 36, the officer didn't have enough information. Then he was told that the sum is equal to number of shops in front of the office. He replied by saying that this still isn't enough information. So the sum of the ages should be 13, because otherwise he would have known the ages immediately. The last statement is that the oldest child loves chocolate. So there is an oldest child. Hence the officer concludes that the ages of the children are 2, 2 and 9 years.
Hence, option (1) is the correct answer.
Skills Required to Solve Quantitative Reasoning Questions
To successfully solve quantitative reasoning questions, several key skills are essential:
1. Understanding Specific Logic: Being able to grasp the particular numerical logic presented in the questions.
2. Ordering Clues Correctly: Arranging the given clues in the right sequence, following the principles of logical reasoning.
3. Understanding Basic Math Concepts: Familiarity with fundamental mathematical concepts such as percentages, averages, ratios, and multiplication.
4. Creating Symbolic Representations: The skill to represent clues symbolically, making it easier to combine and analyze relevant information.
5. Timing and Patience: Knowing when to utilize indirect clues provided in the question and waiting for the appropriate moment during problem-solving.
Examples
Q1: 5, 11, 24.2, 53.24, ?, 257.6816
Sol:
5 x 2.2 = 11
11 x 2.2 = 24.2
24.2 x 2.2 = 53.24
53.24 x 2.2 = 117.128
117.128 x 2.2 = 257.6816
Hence, the correct answer is 117.128.
Q2: 71 : 42 :: 98 : ?
Sol:
71 – 29 = 42
Similar, 98 – 29 = 69
Hence, 69 will replace the question mark.
Q3: 71 : 42 :: 98 : ?
Sol:
71 – 29 = 42
Similar, 98 – 29 = 69
Hence, 69 will replace the question mark.
Q4: 67 : 76 :: 42: ?
Sol:
67 + 9 = 76
Similarly, 42 + 9 = 51,
Hence, 51 will replace the question mark.
Q5: 49, 121, 169, ?, 361
Sol: The solution of the series is as follows.
72 = 49
112 = 121
132 = 169
172 = 289
192 = 361
Hence, the correct answer is 289.
Q6: The position of how many digit(s) in the number 381576 will remain the same after the number is arranged in the ascending order?
Sol:
Original number form is: 3 8 1 5 7 6
Ascending order form is: 1 3 5 6 7 8
If we check the number/s whose position will remain the same in both forms then we will see that the position of only number remains same or unchanged which is the number 7.
Hence, the correct answer is One.
Q7: If 3x - 7 = 20, what is the value of x?
Sol: 3x - 7 = 20 3x = 20 + 7 3x = 27 x = 27 / 3 x = 9
Q8: A car travels 360 miles in 6 hours. What is its average speed?
Sol: Average speed = Total distance / Total time Average speed = 360 miles / 6 hours Average speed = 60 miles per hour
Q9: What is 35% of 120?
Sol: 35% of 120 = (35/100) * 120 = 42
Q10: If the area of a rectangle is 180 square units and its length is 12 units, what is its width?
Sol: Area of a rectangle = length * width 180 = 12 * width width = 180 / 12 width = 15 units
Q11: Solve for y: 4y + 5 = 3y + 12
Sol: 4y + 5 = 3y + 12 4y - 3y = 12 - 5 y = 7
Q12: In a class of 40 students, 12 students are girls. What percentage of the class is made up of girls?
Sol: Percentage of girls = (Number of girls / Total students) * 100 Percentage of girls = (12 / 40) * 100 Percentage of girls = 30%
Q13: A store is offering a 25% discount on a jacket that originally costs $80. What is the sale price of the jacket?
Sol: Discount amount = 25% of $80 = (25/100) * $80 = $20 Sale price = Original price - Discount amount Sale price = $80 - $20 = $60
Q14: If a train travels at 75 miles per hour for 2 hours and 45 minutes, how far does it travel?
Sol: Time in hours: 2 hours + (45 minutes / 60 minutes) = 2.75 hours Distance = Speed * Time Distance = 75 miles/hour * 2.75 hours = 206.25 miles
Q15: What is the sum of the first ten positive odd numbers?
Sol: The first ten positive odd numbers are: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 Sum = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100
Q16: A rectangular garden has a perimeter of 60 meters, and its width is 10 meters. What is its length?
Sol: Perimeter of a rectangle = 2 * (length + width) 60 = 2 * (length + 10) 30 = length + 10 Length = 20 meters
Q17: If the sum of three consecutive even numbers is 78, what is the largest number?
Sol: Let the numbers be x, x+2, and x+4. x + (x+2) + (x+4) = 78 3x + 6 = 78 3x = 72 x = 24 The largest number is x + 4 = 24 + 4 = 28
Q18: A fruit seller sold 120 kg of apples at $4 per kg and 80 kg of oranges at $5 per kg. How much money did he earn in total?
Sol: Money from apples = 120 kg * $4 = $480 Money from oranges = 80 kg * $5 = $400 Total money earned = $480 + $400 = $880
Q19: What is the smallest positive integer that is divisible by both 6 and 8?
Sol: Find the least common multiple (LCM) of 6 and 8. Prime factors of 6 = 2 * 3 Prime factors of 8 = 23 LCM = 23 * 3 = 24 The smallest positive integer is 24.
Q20: Solve the following equation: 5(x - 3) = 4(x + 2)
Sol: 5(x - 3) = 4(x + 2) 5x - 15 = 4x + 8 5x - 4x = 15 + 8 x = 23
Q21: A car rental company charges $20 per day plus an additional $0.15 per mile driven. How much would it cost to rent a car for 3 days and drive 200 miles?
Sol: Cost for 3 days = 3 * $20 = $60 Cost for 200 miles = 200 * $0.15 = $30 Total cost = $60 + $30 = $90
Q22: If 9 books weigh 36 pounds, how much would 15 books weigh?
Sol: Weight of 1 book = 36 pounds / 9 books = 4 pounds/book Weight of 15 books = 15 books * 4 pounds/book = 60 pounds
Q23: What is the average of the numbers 18, 24, and 30?
Sol: Average = (Sum of numbers) / (Number of numbers) Average = (18 + 24 + 30) / 3 Average = 72 / 3 = 24
Q24: If a square has a side length of 8 units, what is the length of its diagonal?
Sol: Diagonal length = Side length * √2 Diagonal length = 8 * √2 = 8√2 units
Q25: A store sells packs of 6 pens for $4.50 per pack. How much would 3 packs cost?
Sol: Cost of 3 packs = 3 * $4.50 = $13.50
Q26: A person invests $1000 in a savings account with an annual interest rate of 4% compounded annually. What is the balance in the account after 2 years?
Sol: A = P(1 + r/n)(nt) Where A is the final amount, P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
A = P(1 + r/n)(nt) Where A is the final amount, P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years. A = 1000(1 + 0.04/1)(1*2) A = 1000(1 + 0.04)2 A = 1000(1.04)2 A = 1000 * 1.0816 A = 1081.60
The balance in the account after 2 years is $1081.60.
Arithmetic Reasoning Formulas
Arithmetic reasoning often involves using basic formulas to solve problems. Here's a list of some common arithmetic formulas that can be helpful:
- Addition: a + b = c
- Subtraction: a - b = c
- Multiplication: a * b = c
- Division: a / b = c
- Average: (a + b + c + ... + n) / n
- Percentage: (part/whole) * 100
- Ratio: a: b
- Proportion: a / b = c / d
- Distance: Speed * Time
- Speed: Distance / Time
- Time: Distance / Speed
- Simple Interest: I = P * R * T / 100 (where I = interest, P = principal, R = rate, and T = time)
- Compound Interest: A = P(1 + r/n)(nt) (where A = amount, P = principal, r = annual interest rate, n = number of times interest is compounded per year, and t = time in years)
- Profit or Loss: Profit = Selling Price - Cost Price (Loss = Cost Price - Selling Price)
- Percent Increase or Decrease: (New Value - Old Value) / Old Value * 100
- Fractions:
- Addition: a/b + c/d = (ad + bc) / bd
- Subtraction: a/b - c/d = (ad - bc) / bd
- Multiplication: (a/b) * (c/d) = (a * c) / (b * d)
- Division: (a/b) ÷ (c/d) = (a * d) / (b * c)
- Decimal to Fraction: To convert a decimal to a fraction, write the decimal as the numerator and the denominator as a power of 10 based on the number of decimal places. Then, simplify the fraction.
Fraction to Decimal: Divide the numerator by the denominator.
Fraction to Percentage: (Fraction) * 100
Percentage to Fraction: (Percentage) / 100
Percentage to Decimal: (Percentage) / 100
Decimal to Percentage: (Decimal) * 100
Weighted Average: (w1 * x1 + w2 * x2 + ... + wn * xn) / (w1 + w2 + ... + wn)
Least Common Multiple (LCM): The smallest multiple that is exactly divisible by each of the numbers.
Greatest Common Divisor (GCD): The largest number that divides two or more numbers without leaving a remainder.
Prime Numbers: A number greater than 1 that has only two factors: 1 and itself.
Factors: The numbers that can be multiplied together to get the original number.
Square of a Number: a² = a * a
Cube of a Number: a³ = a * a * a
Square Root: √a is the number that, when multiplied by itself, equals a.
Cube Root: ∛a is the number that, when multiplied by itself three times, equals a.
Permutations: nPr = n! / (n - r)!, where n is the total number of elements and r is the number of elements chosen.
Combinations: nCr = n! / [r!(n - r)!], where n is the total number of elements and r is the number of elements chosen.
These arithmetic formulas cover the basic concepts and can be applied to various problem-solving situations. However, keep in mind that more advanced arithmetic problems might require additional formulas or a combination of these basic formulas.
Types of Arithmetic Reasoning
Let us see the various types of arithmetic reasoning questions that may come in your upcoming competitive exams.
1. Puzzle
In these type of arithmetic reasoning questions, candidates need to analyze the given piece of information, pick the information that is important, and leave out the information that is not required in solving the given set of questions.
2. Analogy
In these type of arithmetic reasoning questions, candidates will need to find a word or paid words analogous to those given in the question.
3. Series
In these type of arithmetic reasoning questions, Candidates need to find the missing or wrong number in the provided series. There may be some questions where one of the terms in the given series will be incorrect, and candidates need to find out that term of the series by identifying the pattern involved in the formation of the series.
4. Inequality
In these type of arithmetic reasoning questions, candidates must know about various signs, which are used in such types of questions. The same is given below: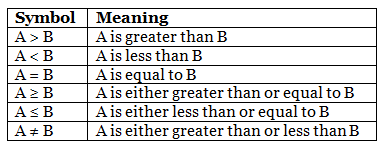
5. Venn Diagram
A Venn Diagram is a representation method for all possible relations that can exist between a given group of elements in a single figure. A venn diagram is the easiest way to express the relationship between sets.
6. Cube & Dice
In these type of arithmetic reasoning questions, problems based on single or multiple cube and dice will be asked and candidates need to give the correct answer by analyzing the given image.
Arithmetic Reasoning Tips and Tricks
Solving arithmetic reasoning questions can be made easier by following a step-by-step approach. Here are some arithmetic reasoning tricks and tips to help you tackle these problems more effectively:
Read the question carefully: Make sure you thoroughly understand the problem statement of the arithmetic reasoning question and identify the information given, as well as what you need to find out.
Break down the problem: Simplify complex arithmetic problems by breaking them into smaller, more manageable parts. Identify the underlying concepts and relationships between the given data.
Choose the right formula or method: Based on the information and relationships identified, select the appropriate arithmetic formula or method to solve the problem.
Organize the data: Arrange the given data and any additional information you've deduced in a structured way. This can be in the form of a table, diagram, or equation.
Perform calculations: Apply the chosen arithmetic formula or method and carry out the necessary calculations. Keep track of units, if applicable, and ensure the accuracy of your calculations.
Check your work: Verify the accuracy of your calculations and ensure that your answer makes logical sense in the context of the problem. If necessary, retrace your steps and identify any errors.
Simplify the answer: If required, simplify your answer by expressing it in the most appropriate format, such as a fraction, decimal, or percentage.
Review the question: Go back to the problem statement and ensure your answer addresses what was asked. If the question has multiple parts, make sure you've addressed all aspects.
|
177 videos|210 docs|199 tests
|
FAQs on Overview: Quantitative Reasoning - General Intelligence and Reasoning for SSC CGL
| 1. What is arithmetic reasoning? |  |
| 2. Why is arithmetic reasoning important? |  |
| 3. How is arithmetic reasoning assessed in exams? |  |
| 4. How can I improve my arithmetic reasoning skills? |  |
| 5. Are there specific strategies for solving arithmetic reasoning questions? |  |
















