Overview: Set Theory | Quantitative Aptitude (Quant) - CAT PDF Download
Representation of Sets
Tabular form of Sets: In this method, a set is characterized by writing components, separated by commas, within the braces{}.
For example, A = {2, 3, 5} is a set of the first three prime numbers.
Set–builder form: In this arrangement, a rule is written in the braces that define the sets.
For example, B = {x : 6 ≤ x ∈ N ≤ 12}.
Types of Sets
The various types of sets are given below:
Empty/Null Set: A set that does not contain any element is termed a null set or Empty Set in Sets Math. It is indicated by ϕ or {}.
Example: A = {x : x is a prime number lying between 90 and 96} = ϕ
Singleton Set: A set that has only one element is termed a singleton set.
Example: A = {0}
Finite Set: A set that contains a finite number of elements is named a finite set in Sets Math.
Example: A = {2, 3, 5}
Infinite Set: A set that has an infinite number of components is named an infinite set in Sets Math.
Example: Z = set of all integers = {0, ± 1, ± 2, …….}
Equivalent Sets: Any two sets are stated to be equivalent sets if their cardinality i.e the number of components present in both sets are the same.
Example: A = {2, 3, 5} and B = {3, 5, 7} are equivalent sets in Sets Math since their cardinality is the same which is 3.
Equal Sets: Any two sets are declared to be equal sets if and only if they are equivalent and as well as their elements are identical.
Example: A = {2, 3, 5} and B = {2, 3, 5} are equal sets since they are equivalent sets as they are possessing the same number of elements plus the elements existing in both sets are the same.
Subset: Consider A and B to be two sets. If each element of A is present in set B then A is designated a subset of B and it is denoted by the notation A ⊆ B.
Example: A = {2, 3, 5} and B = {2, 3, 5, 7}. Here we can recognize that all the components of set A are present in set B. So, A ⊆ B.
Proper Subset: Consider A and B to be two sets. Then A is declared to be a proper subset of B if A is a subset of B and A is not equivalent to B. It is expressed as A ⊂ B.
Example: A = {2, 3, 5} and B = {2, 3, 5, 7}.Here we can see that A is a subset of B and A is not equal to B. So, A ⊂ B.
Power Set: Let A be set, then the set of all the possible subsets of A is called the power set of A and is denoted by P(A).
i.e P(A) = {X : X ⊆ A}
Universal Set: Usually, we deal with the components and subsets in a basic set theory that is relevant to that particular circumstance. For instance, while studying the system of numbers, we are interested in the set of natural numbers and their subsets such as the set of all prime numbers, the set of all even numbers, the set of all odd numbers, and so on.
This basic set is called the “Universal Set”. The universal set is normally indicated by U, and all its subsets are by the letters A, B, C, etc. For example, for the set of all integers, the universal set can be the set of rational numbers, in human population studies, the universal set comprises all the people in the world.
Operations on Sets
The various operations on sets are given below:
Venn Diagrams: Most of the relationships between sets can be interpreted utilizing diagrams recognized as Venn diagrams. Venn diagrams are identified after the English logician, John Venn. These diagrams consist of rectangles and closed curves and regular circles. The universal set is designated by a rectangle and its subsets are denoted by circles. We will get a clear idea about the rectangle and circle concept in the operations below.
Union of Sets: Let A and B be two sets. The union of sets A and B is the set of all those components which belong to either A or B or both A and B. The union of A and B is indicated by A ∪ B.
i.e A ∪ B = {x : x ∈ A or x ∈ B}
⇒ Example: If A = {2, 3, 5} and B = {2, 3, 5, 7}. Then A ∪ B = {2, 3, 5, 7}.
The Venn diagram for the union of any two sets is shown below for a better understanding: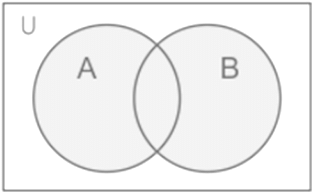
Intersection of Sets: Let A and B be two sets. The intersection of sets A and B is the set of all those components which are present in both sets A and B.
⇒ The intersection of A and B is indicated by A ∩ B i.e A ∩ B = {x: x ∈ A and x ∈ B}
⇒ Example: If A = {2, 3, 5} and B = {2, 3, 5, 7}. Then A ∩ B = {2, 3, 5}
The Venn diagram for intersection is shown below to have a clear idea: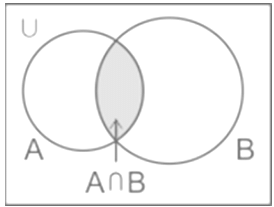
Disjoint Sets: Any two sets say A and B are said to be disjoint if A ∩ B = ϕ i.e they don’t have any common component.
Example: If A = {1, 2, 3} and B = {4, 5, 6, 7}. Then A ∩ B = ϕ
The Venn diagram illustration of disjoint sets is shown below: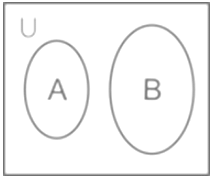
Difference Between two Sets
Let A and B be two sets. The difference between A and B expressed as (A – B) or A \ B, is the set of all those elements of A which are not present in B.
i.e A – B = {x : x ∈ A and x∉ B}
Example: If A = {1, 2, 3, 5, 7} and B = {2, 3, 5}. Then A – B = {1} and B – A = {7}
The Venn diagram representation of the difference between the two sets is shown below:
Symmetric Difference between two Sets
Let A and B be two sets. The symmetric difference of sets A and B is the set (A – B) ∪ (B – A) and is denoted as A Δ B.
i.e A Δ B = (A – B) ∪ (B – A)
⇒ Example: If A = {1, 2, 3, 5, 7} and B = {2, 3, 5}. Then A – B = {1}, B – A = {7} and A Δ B = {1, 7}.
The Venn diagram illustration of the symmetric difference between two sets is presented below: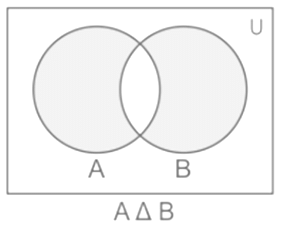
Complement of a Set
Let A be any set. Then complement of set A is denoted by A’ or Ac such that A’ = {x: x ∉ A} = U – A, where U is the universal set.
The Venn diagram illustration of the complement of a set is shown below:
The next concept in line is the laws regarding set theory, the laws and properties always act as a time saver element in solving the numerical during the examination. So let us look at the list of laws of Sets Math one by one.
Laws of Algebra of Sets
Read about the Laws of Algebra of Sets in the table below:
Sets Formulas
Consider A, B and C to be three finite sets and U representing the finite universal set, then;
- n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
- n (A ∪ B) = n (A) + n (B) ⇔ A ∩ B = ϕ
- n (A – B) = n (A) – n (A ∩ B) = n (A ∩ B’)
- n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n(A ∩ B) – n (B ∩ C) – n (A ∩ C) + n (A ∩ B ∩ C)
- n (A’ ∪ B’) = n [(A ∩ B)’] = n (U) – n (A ∩ B)
- n (A’ ∩ B’) = n [(A ∪ B)’] = n (U) – n (A ∪ B)
- n (A Δ B) = n (A) + n (B) – 2 n (A ∩ B)
- n (A’) = n (U) – n (A)
How to Solve Set Theory Questions
While answering Sets Math word problems there are 2 things that we should retain in mind while solving them, first is we need to understand the meaning of the word problem i.e what is given, what requires to be derived, and how to determine the desired outcomes utilizing the given facts.
Or in other words, we can say that while working on word problems there are some keywords whose interpretation should be recognized followed by drawing the Venn diagram for the problem which easily assists us to conclude.
So, let’s have a look at some of the most common keywords used in word problems for Sets Math:
- Either – or: Let’s take an example to understand this suppose two sets A and B are provided to us and we require to find the number of components present in either A or B i.e we need to find out the value of n (A ∪ B).
- Both / All: Let’s take an illustration to understand this suppose two sets P and Q are provided to us and we need to find the number of elements present in both sets A and B i.e we need to find out the value of n (A ∩ B).
- Neither – nor: Let’s take an instance to understand this assume two sets A and B are provided to us and we need to find the number of components that are present neither in A nor in B i.e we ought to find out the value of n [(A ∪ B)’].
- Only: Let’s take an illustration to surmise this suppose two sets A and B are provided to us and we need to find the number of components that are present only in A or only in B i.e we have to find out the value of n (A – B) or n (B – A) respectively.
- Either only – or only: Let’s take an instance to explain this suppose two sets A and B are provided to us and we are required to find the number of components that are present either only in A or only in B i.e we need to find out the value of n (A Δ B).
- Not in: Let’s take an example to understand this: assume two sets A and B are given to us and we require to find the number of components that are not in A or not in B i.e we require to find out the value of n (A’) or n (B’) respectively.
|
167 videos|229 docs|95 tests
|





















