Past Year Questions: Principal Stress & Principal Strain | Solid Mechanics - Mechanical Engineering PDF Download
Q1: Find the correct match between the plane stress states and the Mohr's circles. [2024, Set-I]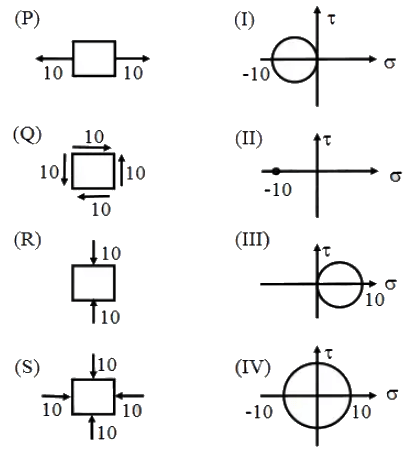
(a) (P)-(I); (Q)-(II); (R)-(III); (S)-(IV)
(b) (P)-(I); (Q)-(IV); (R)-(III); (S)-(II)
(c) (P)-(III); (Q)-(II); (R)-(I); (S)-(IV)
(d) (P)-(III): (Q)-(IV); (R)-(I); (S)-(II)
Ans: (d)
Q2: In a two-dimensional stress analysis, the state of stress at a point is shown in the figure. The values of length of PQ, QR, and RP are 4, 3, and 5 units, respectively. The principal stresses are (round off to one decimal place) [2023, Set-II]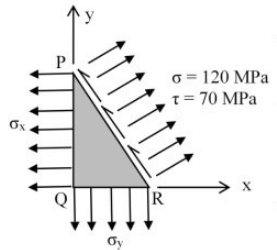 (a) σx =26.7MPa, αy = 172.5MPa
(a) σx =26.7MPa, αy = 172.5MPa
(b) σx =54.0MPa, σy = 128.5MPa
(c) σx =67.5MPa, σy = 213.3MPa
(d) σx =16.0MPa, σy = 138.5MPa
Ans: (c)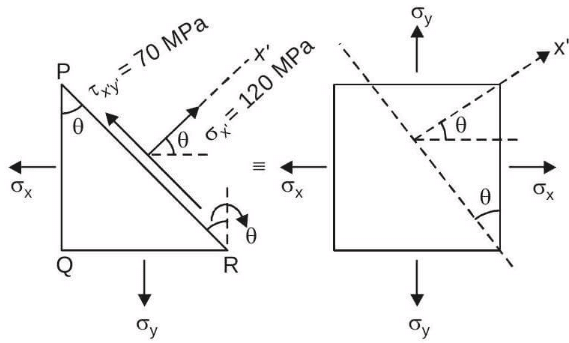
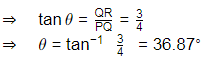
Using transformation equations: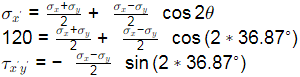
From above equations, we get
σx = 67.5 MPa
σy = 213.3 MPa
Q3: The infinitesimal element shown in the figure (not to scale) represents the state of stress at a point in a body. What is the magnitude of the maximum principal stress (in N/mm2 , in integer) at the point? [2023, Set-I]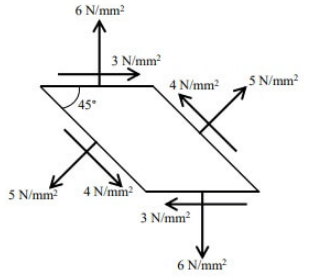 (a) 4
(a) 4
(b) 5
(c) 7
(d) 9
Ans: (c)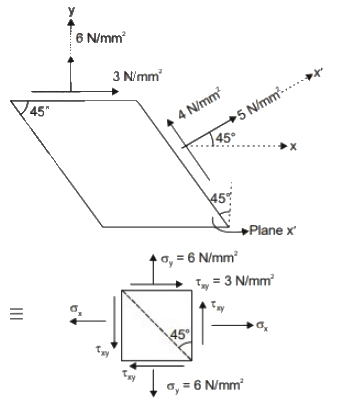
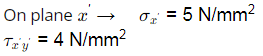
Using transformation equations: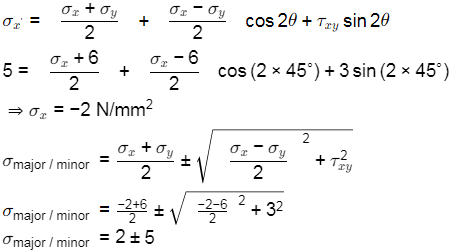
⇒ σ major =7 N/mm2 ,σ minor =−3MPa
Hence, magnitude of maximum principal stress is 7 N/mm2.
Q4: A hanger is made of two bars of different sizes. Each bar has a square cross-section. The hanger is loaded by three-point loads in the mid vertical plane as shown in the figure. Ignore the self-weight of the hanger. What is the maximum tensile stress in N/mm2 anywhere in the hanger without considering stress concentration effects? [2023, Set-I]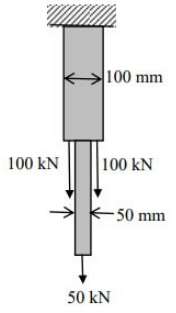
(a) 15
(b) 25
(c) 35
(d) 45
Ans: (b)
FBD
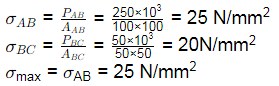
Q5: Stresses acting on an infinitesimal soil element are shown in the figure (with σz > σx). The major and minor principal stresses are σ1 and σ3 , respectively. Considering the compressive stresses as positive, which one of the following expressions correctly represents the angle between the major principal stress plane and the horizontal plane? [2022, Set-II]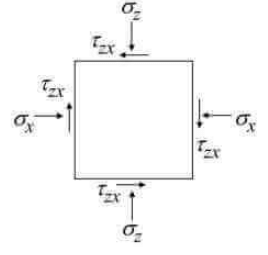 (a)
(a)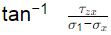
(b)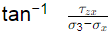
(c)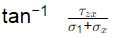
(d)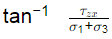
Ans: (a)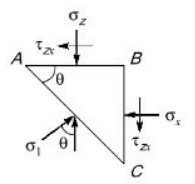
∑Fx = 0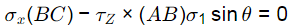

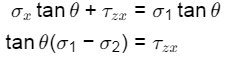
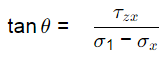
Q6: The state of stress in a deformable body is shown in the figure. Consider transformation of the stress from the x-y coordinate system to the X-Y coordinate system. The angle θ, locating the X-axis, is assumed to be positive when measured from the x-axis in counter-clockwise direction. [2021, Set-I]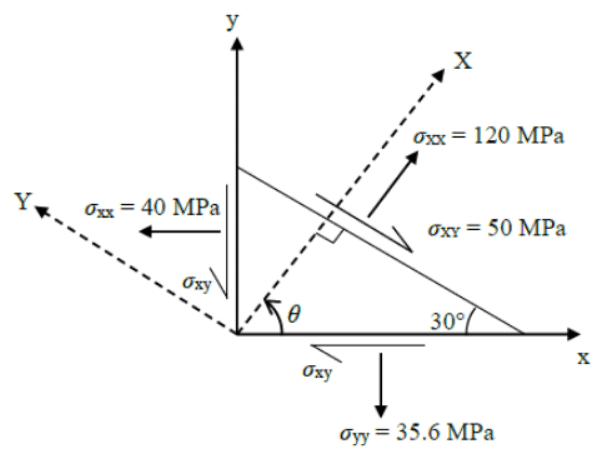 The absolute magnitude of the shear stress component σxy (in MPa,round off to one decimal place) in x-y coordinate system is ________________
The absolute magnitude of the shear stress component σxy (in MPa,round off to one decimal place) in x-y coordinate system is ________________
(a) 96.2
(b) 54.6
(c) 48.2
(d) 28.7
Ans: (a)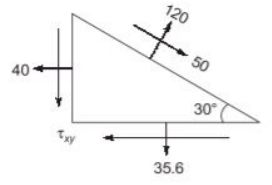
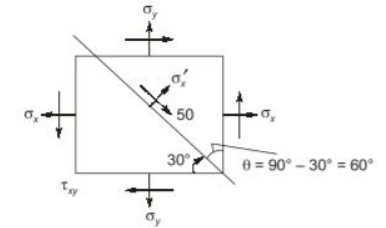
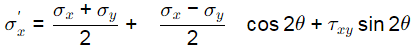
Here θ = 60º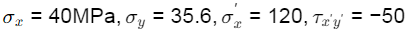
Substituting the values in above equation, we get
τxy = 96.186 MPa
Q7: In a two-dimensional stress analysis, the state of stress at a point P is [2020, Set-I]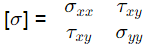
The necessary and sufficient condition for existence of the state of pure shear at the point P, is
(a) 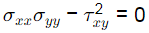
(b) τxy = 0
(c) σxx + σyy = 0
(d)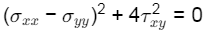
Ans: (c)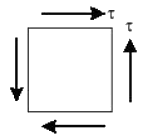 In pure shear condition σx = 0, σy = 0, τxy = τ
In pure shear condition σx = 0, σy = 0, τxy = τ For this condition σxx + σyy = 0 is true.
For this condition σxx + σyy = 0 is true.
Q8: For a plane stress problem, the state of stress at a point P is represented by the stress element as shown in figure.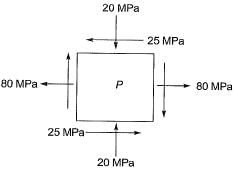 By how much angle (θ) in degrees the stress element should be rotated in order to get the planes of maximum shear stress? [2019 : 2 Marks, Set-II]
By how much angle (θ) in degrees the stress element should be rotated in order to get the planes of maximum shear stress? [2019 : 2 Marks, Set-II]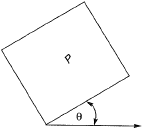 (a) 31.7
(a) 31.7
(b) 13.3
(c) 26.6
(d) 48.3
Ans: (a)
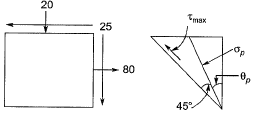
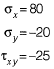
Angle of plane of max shear
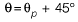
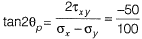
∴ 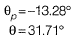
Q9: An element is subjected to biaxial normal tensile strains of 0.0030 and 0.0020. The normal strain in the plane of maximum shear strain is [2019 : 1 Mark, Set-I]
(a) Zero
(b) 0.0050
(c) 0.0010
(d) 0.0025
Ans: (d)
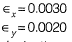
Normal strain in the plane of maximum shear strain
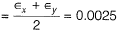
Q10: For the stress state (in MPa) shown in the figure, the major principal stress is 10 MPa.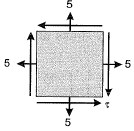 The shear stress τ is [2016 : 2 Marks, Set-II]
The shear stress τ is [2016 : 2 Marks, Set-II]
(a) 10.0 MPa
(b) 5.0 MPa
(c) 2.5 MPa
(d) 0.0 MPa
Ans: (b)
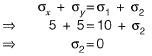
Now,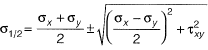
∴ 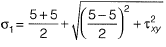
⇒ 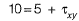
∴ 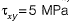
Q11: For the plane stress situation shown in the figure, the maximum shear stress and the plane on which it acts are [2015 : 1 Mark, Set-II]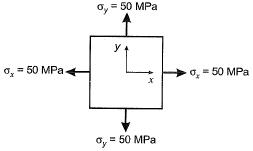 (a) -50 MPa, on a plane 450 clockwise w.r.t. x-axis
(a) -50 MPa, on a plane 450 clockwise w.r.t. x-axis
(b) -50 MPa, on a plane 450 anti-clockwise w.r.t. x-axis
(c) 50 MPa, at all orientations
(d) Zero, at all orientations
Ans: (d)
Under hydrostatic loading condition, stresses at a point in all directions are equal and hence no shear stress.
Alternatively,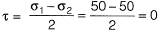
Thus, Mohr’s circle reduces to a point. Hence shear stress at all orientations is zero.
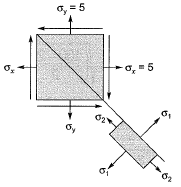
Q12: Two triangular wedges are glued together as shown in the following figure. The stress acting normal to the interface, σ∩ is __________MPa. [2015 : 1 Mark, Set-I]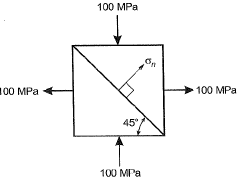 Ans:
Ans:
As plane ABand BCare principle planes, therefore Mohr’s circle for the given condition is, Here, normal stress is zero at 450 to the principle plane.
Here, normal stress is zero at 450 to the principle plane.
Method-ll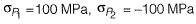
⇒ at 450, it is a plane of maximum shear stress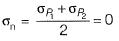
Q13: The state of 2D stress at a point is given by a matrix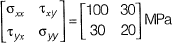
The maximum shear stress in MPa is [2013 : 2 Marks]
(a) 50
(b) 75
(c) 100
(d) 110
Ans: (a)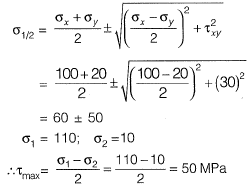
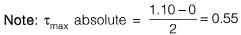
But SS is not the option so taken (τmax)plain otherwise prefer (τmax)absolute.
Q14: If a small concrete cube is submerged deep in still water in such a way that the pressure exerted on all faces of the cube is p, then the maximum shear stress developed inside the cube is [2012 : 1 Mark]
(a) 0
(b) p/2
(c) p
(d) 2p
Ans: (a)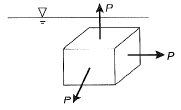 Maximum shear stress,
Maximum shear stress,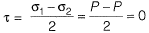
Note: It is the case of hdyrostatic force, Mohr circle of which is a point hence τmax = 0.
Q15: The major and minor principal stresses at a point are 3 MPa and - 3 MPa respectively. The maximum shear stress at the point is [2010 : 1 Mark]
(a) zero
(b) 3 MPa
(c) 6 MPa
(d) 9 MP
Ans: (b)
Method-I
Maximum shear stress at the point is given by,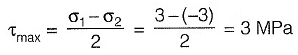
Method-II
By Mohr Cicle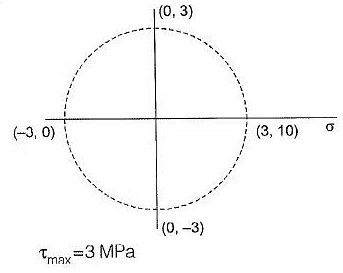
|
33 videos|72 docs|29 tests
|
FAQs on Past Year Questions: Principal Stress & Principal Strain - Solid Mechanics - Mechanical Engineering
| 1. What are principal stresses and how are they calculated? |  |
| 2. What is the significance of principal strain in engineering? |  |
| 3. How can principal stresses be visualized using Mohr's Circle? |  |
| 4. What are the common methods used to determine principal stresses in practice? |  |
| 5. How do temperature changes affect principal stresses and strains? |  |





















