Mechanical Engineering Exam > Mechanical Engineering Notes > Solid Mechanics > Past Year Questions: Theory of Column & Shear Centre
Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering PDF Download
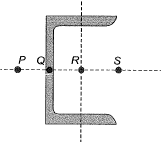
Q1: For a thin-walled section shown in the figure, points P, Q and R are located on the major bending axis X−X of the section. Point Q is located on the web whereas point S is located at the intersection of the web and the top flange of the section. [2024, Set-II]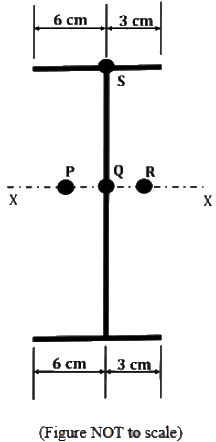
Qualitatively, the shear center of the section lies at
(a) S
(b) R
(c) Q
(d) P
Ans: (b)
Position of shear centre will be at R.
Q2: Consider the cross-section of a beam made up of thin uniform elements having thickness t(t<<a) shown in the figure. The (x, y) coordinates of the points along the center-line of the cross-section are given in the figure. [2022, Set-I]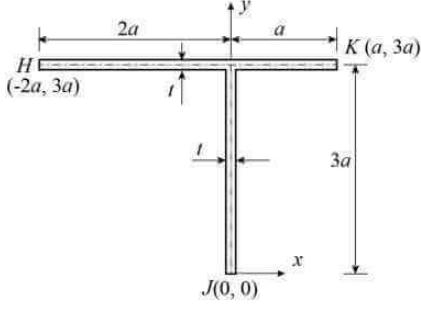
The coordinates of the shear center of this cross-section are:
(a) x = 0, y = 3a
(b) x = 2a, y = 2a
(c) x = -a, y = 2a
(d) x = -2a, y = a
Ans: (a)
Shear centre of section consisting of two intersecting narrow rectangles always lies at the intersection of centrelines of two rectangles.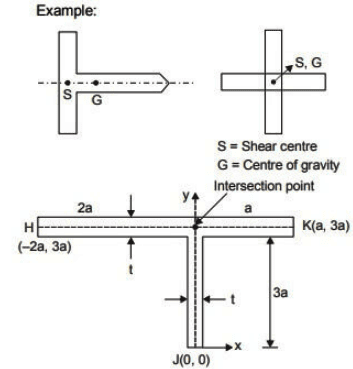
Coordinate of shear centre (0, 3a).
Q3: A column of height h with a rectangular cross-section of size a x 2a has a buckling load of P. If the cross-section is changed to 0.5 a x 3a and its height changed to 1.5h, the buckling load of the redesigned column will be [2018 : 1 Mark, Set-I]
(a) P/12
(b) P/4
(c) P/2
(d) 3P/4
Ans: (a)
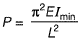
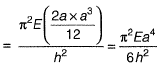
For new column,
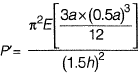
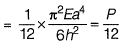
Q4: Consider two axially loaded columns, namely, 1 and 2, made of a linear elastic material with Young’s modulus 2 x 105 MPa, square cross- section with side 10 mm, and length 1 m. For Column 1, one end is fixed and the other end is free. For Column 2, one end is fixed and the other end is pinned. Based on the Euler’s theory, the ratio (up to one decimal place) of the buckling load of Column 2 to the buckling load of Column 1 is _____. [2017 : 2 Marks, Set-I]
Ans:
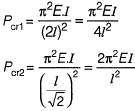
∴ Required ratio =
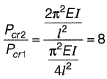
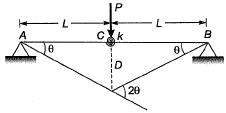
Q5: In a system two connected rigid bars AC and BC are of identical length, L with pin supports at A and B. The bars are interconnected at C by a frictionless hinge. The rotation of the hinge is restrained by a rotational spring of stiffness, k. The system initially assumes a straight line configuration, ACB. Assuming both the bars as weightless, the rotation at supports, A and B, due to a transverse load, P applied at C is [2015 : 2 Marks, Set-II]
(a) PL/4k
(b) PL/2k
(c) P/4k
(d) Pk/4L
Ans: (a)
Deflection under load P= θL
Work done by force
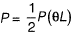
Strain energy stored in spring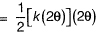
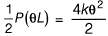
⇒ θ = PL/4k
Q6: If the following equation establishes equilibrium in slightly bent position, the mid-span deflection of a member shown in the figure is
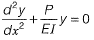
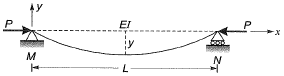If a is amplitude constant for y, then [2014 : 2 Marks, Set-I]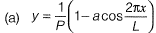
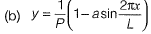
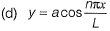
Ans. (C)
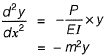
∴ Solution of above differential equation is,
y = a sin mx + b cos mx
at = x = 0, y = 0
⇒ b = 0
at x = L, y = 0
⇒ 0 = sin mL
⇒ mL = nπ
⇒
∴
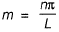
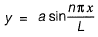
Q7: The possible location of shear centre of the channel section, shown below is, [2014 : 1 Mark, Set-I]
(a) P(b) Q
(c) P
(d) S
Ans: (a)
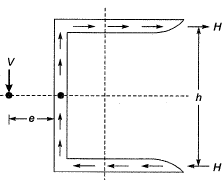For no twistingV x e = H x h
⇒
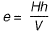
Hence possible location of shear centre is P.
Q8: Two steel column P (length L and yield strength fy = 250 MPa) and Q (length 2L and yield strength fy = 500 MPa) have the same cross-section and end condition the ratio of buckling load of column P to that of column Q is [2013 : 1 Mark]
(a) 0.5
(b) 1.0
(c) 2.0
(d) 4.0
Ans: (d)
Buckling load,
∴
∴
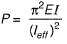
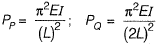
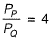
Q9: The ratio of the theoretical critical buckling load for a column with fixed ends to that of another column with the same dimensions and material, but with pinned ends, is equal to [2012 : 1 Mark]
(a) 0.5
(b) 1.0
(c) 2.0
(d) 4.0
Ans: (d)
Eulars critical load,
The document Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering is a part of the Mechanical Engineering Course Solid Mechanics.
All you need of Mechanical Engineering at this link: Mechanical Engineering
|
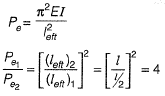
33 videos|27 docs|29 tests
|
FAQs on Past Year Questions: Theory of Column & Shear Centre - Solid Mechanics - Mechanical Engineering
| 1. What is the theory of columns in structural engineering? |  |
Ans.The theory of columns in structural engineering refers to the study of how vertical members (columns) support loads and resist buckling. It includes understanding axial loads, lateral stability, and the material properties that affect column performance. Key concepts include Euler's buckling theory, which predicts the critical load at which a column becomes unstable, and the importance of slenderness ratio in determining a column's behavior under load.
| 2. How do you determine the shear centre of a structural section? | |
Ans.The shear centre of a structural section is the point where the application of shear forces does not cause the section to rotate. To determine the shear centre, engineers typically analyze the distribution of shear flow across the section and calculate the centroid of the shear area. This involves using the geometrical properties of the section and applying principles of static equilibrium to find the location where the resultant shear forces act.
| 3. Why is the shear centre important in design? | |
Ans.The shear centre is crucial in design because it helps prevent unwanted rotations of structural members under shear loads. If the load is applied away from the shear centre, it can induce twisting or bending moments, leading to potential structural failure. Understanding the location of the shear centre allows engineers to ensure that structures behave predictably and safely under various loading conditions.
| 4. What factors affect the load-carrying capacity of columns? | |
Ans.The load-carrying capacity of columns is influenced by several factors, including the column's material properties (such as yield strength and modulus of elasticity), its geometric properties (cross-sectional area, moment of inertia, and slenderness ratio), and the type of loading (axial, eccentric, or lateral). Additionally, boundary conditions and the presence of imperfections can also impact a column's performance under load.
| 5. What is the difference between short and slender columns? | |
Ans.Short columns are those that are relatively thick and have a low slenderness ratio, which means they primarily fail by yielding under axial loads. Slender columns, on the other hand, have a high slenderness ratio and are prone to buckling under axial loads before yielding occurs. Understanding this distinction is essential for engineers to apply the correct design equations and safety factors when analyzing column behavior.
Related Exams
About this Document
|
4.92/5 Rating |
|
Nov 17, 2024 Last updated |
Document Description: Past Year Questions: Theory of Column & Shear Centre for Mechanical Engineering 2024 is part of Solid Mechanics preparation.
The notes and questions for Past Year Questions: Theory of Column & Shear Centre have been prepared according to the Mechanical Engineering exam syllabus. Information about Past Year Questions: Theory of Column & Shear Centre covers topics
like and Past Year Questions: Theory of Column & Shear Centre Example, for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Past Year Questions: Theory of Column & Shear Centre.
Introduction of Past Year Questions: Theory of Column & Shear Centre in English is available as part of our Solid Mechanics
for Mechanical Engineering & Past Year Questions: Theory of Column & Shear Centre in Hindi for Solid Mechanics course.
Download more important topics related with notes, lectures and mock test series for Mechanical Engineering
Exam by signing up for free. Mechanical Engineering: Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering
Description
Full syllabus notes, lecture & questions for Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering - Mechanical Engineering | Plus excerises question with solution to help you revise complete syllabus for Solid Mechanics | Best notes, free PDF download
Information about Past Year Questions: Theory of Column & Shear Centre
In this doc you can find the meaning of Past Year Questions: Theory of Column & Shear Centre defined & explained in the simplest way possible. Besides explaining types of
Past Year Questions: Theory of Column & Shear Centre theory, EduRev gives you an ample number of questions to practice Past Year Questions: Theory of Column & Shear Centre tests, examples and also practice Mechanical Engineering
tests
|
Explore Courses for Mechanical Engineering exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Previous Year Questions with Solutions
,study material
,Viva Questions
,Free
,past year papers
,Exam
,Important questions
,Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering
,Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering
,practice quizzes
,Past Year Questions: Theory of Column & Shear Centre | Solid Mechanics - Mechanical Engineering
,Semester Notes
,ppt
,MCQs
,mock tests for examination
,Summary
,Sample Paper
,shortcuts and tricks
,video lectures
,Extra Questions
,Objective type Questions
;
Additional Information about Past Year Questions: Theory of Column & Shear Centre for Mechanical Engineering Preparation
Past Year Questions: Theory of Column & Shear Centre Free PDF Download
The Past Year Questions: Theory of Column & Shear Centre is an invaluable resource that delves deep into the core of the Mechanical Engineering exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Past Year Questions: Theory of Column & Shear Centre now and kickstart your journey towards success in the Mechanical Engineering exam.
Importance of Past Year Questions: Theory of Column & Shear Centre
The importance of Past Year Questions: Theory of Column & Shear Centre cannot be overstated, especially for Mechanical Engineering aspirants.
This document holds the key to success in the Mechanical Engineering exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Past Year Questions: Theory of Column & Shear Centre Notes
Past Year Questions: Theory of Column & Shear Centre Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Past Year Questions: Theory of Column & Shear Centre.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Past Year Questions: Theory of Column & Shear Centre Notes on EduRev are your ultimate resource for success.
Past Year Questions: Theory of Column & Shear Centre Mechanical Engineering
The "Past Year Questions: Theory of Column & Shear Centre Mechanical Engineering Questions" guide is a valuable resource for all aspiring students preparing for the
Mechanical Engineering exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Past Year Questions: Theory of Column & Shear Centre on the App
Students of Mechanical Engineering can study Past Year Questions: Theory of Column & Shear Centre alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Past Year Questions: Theory of Column & Shear Centre,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Past Year Questions: Theory of Column & Shear Centre is prepared as per the latest Mechanical Engineering syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup