Patterns Around Us Class 4 Notes Maths Chapter 3 Free PDF
| Table of contents |

|
| Introduction |

|
| Let's Begin with a Story |

|
| Patterns with Money |

|
| Even and Odd Numbers |

|
| Some Solved Examples |

|
Introduction
In this chapter, we will explore the fascinating world of patterns that surround us in our daily lives. From counting objects to arranging money, from identifying even and odd numbers to recognizing patterns in arrangements - patterns are everywhere!
Patterns help us organize information, make predictions, and solve problems more efficiently. They are the building blocks of mathematics and help us understand the world around us. Whether you're counting coconut trees or arranging coins in groups, patterns make these tasks easier and more fun.
 Coconut Trees arranged in a pattern
Coconut Trees arranged in a pattern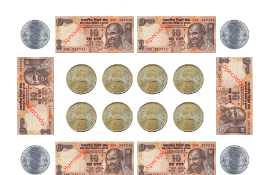 Coins in Patterns
Coins in Patterns
Let's dive into the world of patterns and discover how they shape our understanding of numbers and arrangements!
Let's Begin with a Story
Let us Count - Raju's Pattern Adventure
Raju loved to collect and organize things. One day, while helping his grandmother in the kitchen, he noticed something interesting about the way she arranged fruits in a basket.
"Grandmother, why do you always place the fruits in this circular pattern?" Raju asked.
His grandmother smiled and replied, "Patterns help us organize things better, Raju. Look at how I've arranged these fruits - one apple in the center, surrounded by eight oranges. This pattern not only looks beautiful but also helps me count them easily."

Raju was fascinated. He began to notice patterns everywhere - in the arrangement of trees in the garden, in the design of floor tiles, and even in the way his teacher organized students for group activities.
Soon, Raju started creating his own patterns with different objects. He realized that patterns make counting easier and help us understand relationships between numbers.
Just like Raju, let's explore various patterns in our daily life and learn how they help us understand mathematics better!
Patterns with Money
Money provides an excellent way to understand patterns and practice counting. Let's explore some interesting money patterns.
Pattern 1: Flower Pattern with Coins
In this pattern, coins are arranged in a flower-like shape with one coin in the center and coins arranged around it. Flower - Shape Pattern
Flower - Shape Pattern
Pattern 2: Rectangle Pattern with Notes and Coins
In this pattern, notes and coins are arranged in a rectangular shape.
 Rectangular Shape pattern
Rectangular Shape pattern
Two Ways of Arranging Coins
Shirley and Shiv arranged their coins in the following ways. Let's examine the number of coins in each arrangement.
Coin Arrangements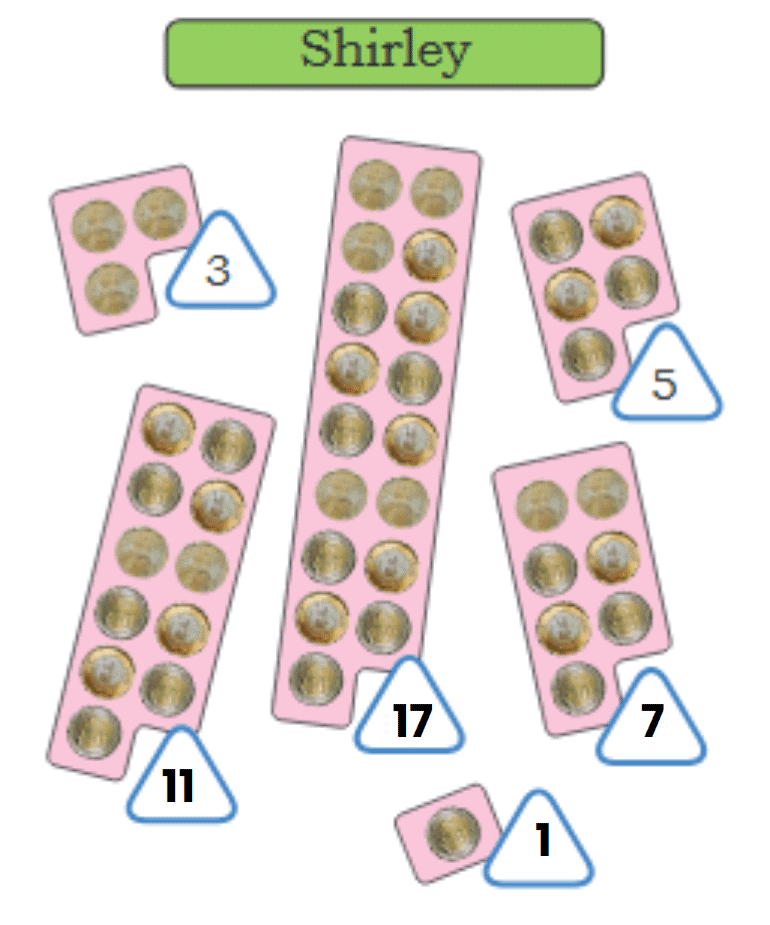 Shirley's Arrangement (Odd Numbers)
Shirley's Arrangement (Odd Numbers)
Shirley arranged her coins in groups of 3, 5, 7, etc. These are odd numbers.
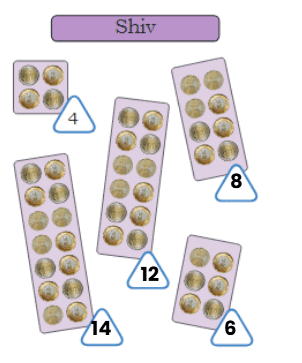 Shiv's Arrangement (Even Numbers)
Shiv's Arrangement (Even Numbers)
Shiv arranged his coins in groups of 4, 6, 8, etc. These are even numbers.
This arrangement helps us understand the concept of odd and even numbers, which we'll explore in more detail in the next section.
Even and Odd Numbers

Even Numbers
Look at the number 4 on the left side of the image. There are 4 ice cream cones.
We can divide them into two equal groups:
2 cones in one group
2 cones in the other group
That means 4 is an even number because it can be split equally into two groups with nothing left over.
So, Even numbers are numbers that can be divided into two equal parts.
Examples of even numbers: 2, 4, 6, 8, 10
Odd Numbers
Now look at the number 5 on the right side. There are 5 cupcakes.
When we try to divide them into two groups:
2 cupcakes go in one group
2 cupcakes go in the second group
But 1 cupcake is left over
That means 5 is an odd number because it cannot be split into two equal groups without something being left out.
So, Odd numbers are numbers that cannot be divided equally into two parts.
Examples of odd numbers: 1, 3, 5, 7, 9
Q1: Do you think all numbers in the times-2 table are even?
Sol: Yes, all numbers in the times-2 table are even numbers. This is because when we multiply any number by 2, we are essentially creating pairs, which is the definition of an even number.
For example:
1 × 2 = 2 (1 pair)
2 × 2 = 4 (2 pairs)
3 × 2 = 6 (3 pairs)
4 × 2 = 8 (4 pairs)
5 × 2 = 10 (5 pairs)

Sol: The times-3 table follows a pattern of odd, even, odd, even, and so on:
1 × 3 = 3 (odd)
2 × 3 = 6 (even)
3 × 3 = 9 (odd)
4 × 3 = 12 (even)
5 × 3 = 15 (odd)
This happens because when we multiply an odd number by 3, we get an odd number, and when we multiply an even number by 3, we get an even number.
Q2: Are there more even or odd numbers between 1 and 100?
Sol: Let's analyze this systematically:
Even numbers between 1 and 100: 2, 4, 6, 8, ..., 98, 100
Odd numbers between 1 and 100: 1, 3, 5, 7, ..., 97, 99
Counting them:
Even numbers: 2, 4, 6, ..., 98, 100 → 50 numbers
Odd numbers: 1, 3, 5, ..., 97, 99 → 50 numbers
Therefore, there are an equal number of even and odd numbers between 1 and 100.

Sol: The possible 2-digit numbers are:
16 (which is even because it ends in 6)
61 (which is odd because it ends in 1)
Let's Try!

This activity helps us understand that a number is even if its last digit is even, and a number is odd if its last digit is odd.
Some Solved Examples
Example 1: Rahul has 5 ₹10 notes, 3 ₹5 coins, and 7 ₹2 coins. How much money does he have in total?
Sol: Amount from ₹10 notes = 5 × ₹10 = ₹50
Amount from ₹5 coins = 3 × ₹5 = ₹15
Amount from ₹2 coins = 7 × ₹2 = ₹14
Total amount = ₹50 + ₹15 + ₹14 = ₹79
Example 2: Sita has 45 candies. She wants to distribute them equally among her friends. Can she distribute them equally among 2 friends? What about 3 friends? Explain your reasoning.
Sol: For 2 friends:
45 ÷ 2 = 22 remainder 1
Since there is a remainder, she cannot distribute them equally among 2 friends.
For 3 friends:
45 ÷ 3 = 15 remainder 0
Since there is no remainder, she can distribute them equally among 3 friends, giving 15 candies to each friend.
This is because 45 is an odd number (not divisible by 2) but is divisible by 3.
Example 3: Observe the given pattern and draw the next three shapes in this pattern.
Sol:
This is an example of a repeating pattern with a cycle of 3 shapes.
|
54 videos|186 docs|14 tests
|
FAQs on Patterns Around Us Class 4 Notes Maths Chapter 3 Free PDF
| $1. What are patterns, and why are they important in our daily lives? |  |
| $2. Can you give examples of patterns found in nature? |  |
| $3. How can we identify patterns in numbers? |  |
| $4. What role do patterns play in art and design? |  |
| $5. How can we create our own patterns at home or school? |  |
















