Perimeter and Area Class 7 Notes Maths Chapter 9
| Table of contents |

|
| Area of Parallelograms |

|
| Area of Triangle |

|
| Circles |

|
| Circumference of Circle |

|
Understanding & Calculating Perimeter
To cover the boundaries of a garden with flowers, you need to calculate the perimeter. The perimeter is the total distance around the garden. Example: For a rectangular garden, add up all the sides:
- Lengths of the sides: 16.3 m, 16.7 m, 16.3 m, 16.7 m
- Perimeter = 16.3 m + 16.7 m + 16.3 m + 16.7 m = 66 m
The perimeter of the rectangle is 66 meters.
Understanding & Calculating Area
The area is the amount of space inside a shape. For a rectangle, it is found by multiplying the length by the width.
Example: For the same rectangle:
- Length = 16.3 m
- Width = 16.7 m
- Area = Length × Width = 16.3 m × 16.7 m = 272.21 m²
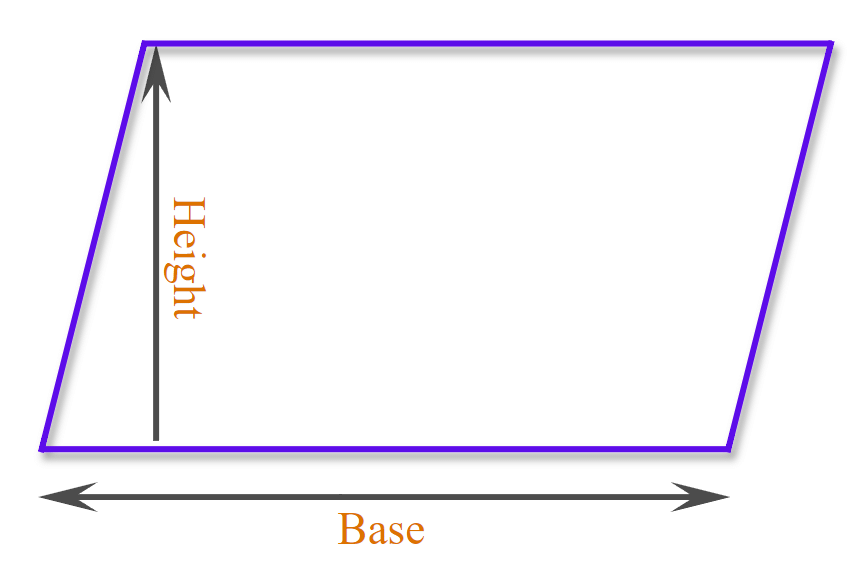
Area of Parallelograms
A parallelogram is a two-dimensional geometrical shape whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length.
To find the area of a parallelogram, you can follow these steps:
- Choose a base (any one side of the parallelogram).
- Determine the height (the perpendicular distance from the base to the opposite side).
- Use the formula: Area = Base × Height

Example Calculations:
Example 1: If you have a parallelogram ABCD, where AB is the base and DE is the height (perpendicular to AB), then the area would be given by: Parallelogram ABCD
Parallelogram ABCD
Area of parallelogram ABCD = Base × Height= AB x DE
Example 2: Find the area of the following parallelograms: 
Ans: Base = 8 cm
Height = 3.5 cm
Area of parallelogram = Base × Height
Area of parallelogram = 8 cm x 3.5 cm = 28 cm2
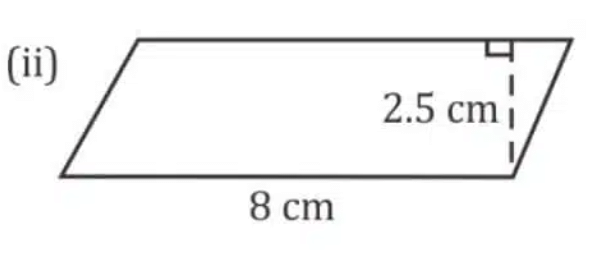 Ans: Base = 8 cm
Ans: Base = 8 cm
Height = 2.5 cm
Area of parallelogram = Base × Height
Area of parallelogram = 8 cm x 2.5 cm = 20 cm2
Example 3: PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallegram PQRS
(b) QN, if PS = 8 cm
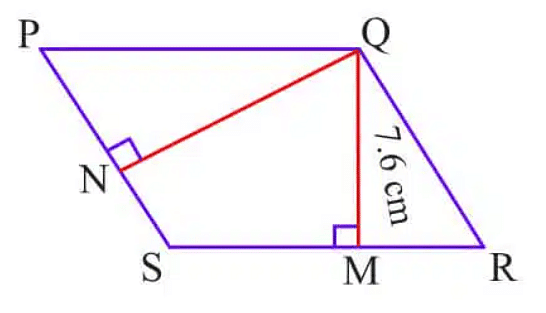
Ans: Given: SR=12 cm, QM = 7.6 cm, PS = 8cm
(a) Area of parallelogram = base x height = 12 x 7.6 = 91.2 cm2
(b) Area of parallelogram = base x height
=> 91.2 = 8 x QN => QN = 91.2/8 = 11.4 cm.
Area of Triangle
A triangle is a polygon with three vertices, and three sides or edges that are line segments. A triangle with vertices A, B, and C is denoted as ABC.
Triangle ABC
To find the area of a triangle within a parallelogram, you can follow these steps
1. Identify the Triangle
- Look at one of the triangles inside the parallelogram.
- The base of the triangle is one side of the parallelogram.
- The height is the straight distance from the base to the opposite side.
2. Understand the Relationship
- A parallelogram is made up of two identical triangles.
- Therefore, the area of the parallelogram is twice the area of one triangle.
3. Calculate the Area of the Parallelogram
- Use the formula: Area = Base × Height

4. Apply the Relationship for the Triangle
- Since the parallelogram has two identical triangles, the area of one triangle is half the area of the parallelogram.
 Parallelogram ABCD
Parallelogram ABCD
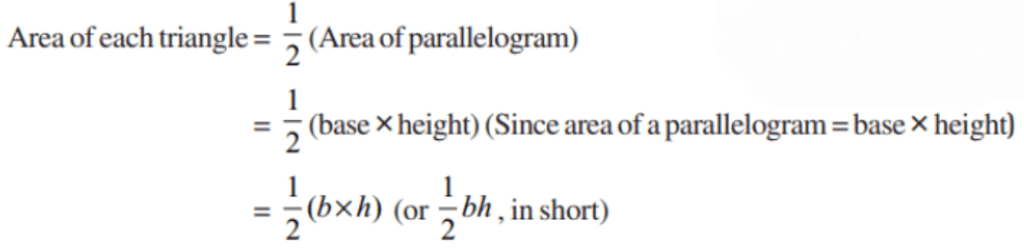
All the congruent triangles are equal in area but the triangles equal in area need not be congruent.
Example 1: Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.
Ans: Height = 3 cm, Area = 36 cm2
Area of the triangle ABC = 1/2 x b x h
=> 36 = 1/2 x b x 3 => b = 24 cm
Base BC = 24 cm
Example 2: Triangle ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of Triangle ABC. What will be the height from C to AB i.e., CE?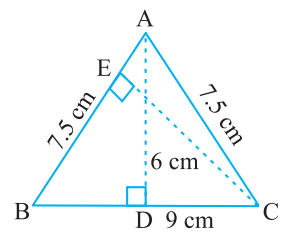
Ans: In triangle ABC, AD = 6cm and BC = 9cm
Area of triangle = 1/2 x base x height = 1/2 x AB x CE
=> 27 = 1/2 x 7.5 x CE
=> CE = (27 x 2) /7.5 => CE = 7.2 cm
Height from C to AB ie.., CE is 7.2 cm
Circles
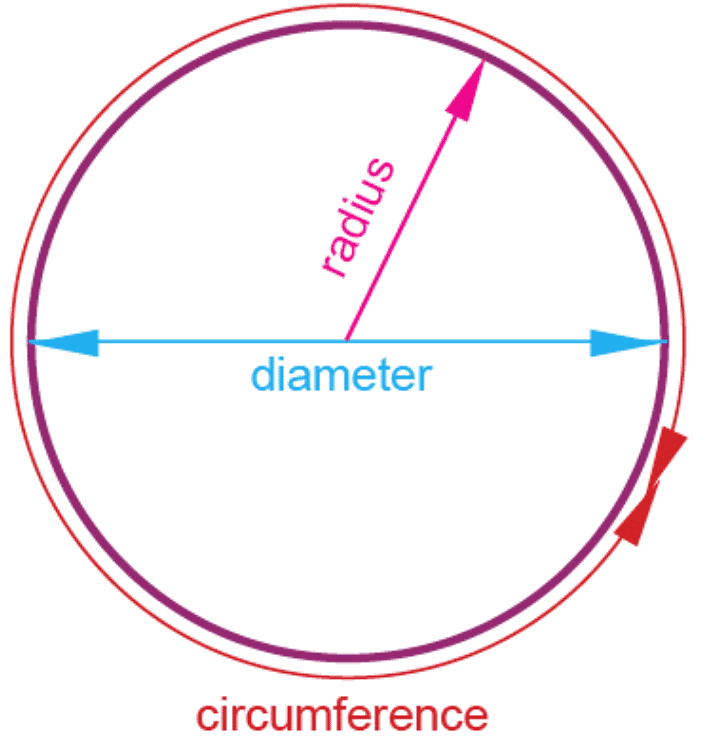
A circle is defined as a collection of points on a plane that are at an equal distance.
 Circle
Circle
- Diameter: Any straight line segment that passes through the centre of a circle and whose end points are on the circle is called its diameter.
- Radius: Any line segment from the centre of the circle to its circumference.
Circumference of Circle
The distance around a circular region is known as its circumference.

where,
- r is the radius of the circle
- π is an irrational number, whose value is approximately equal to 3.14
Circumference = Diameter x 3.14
Diameter(d) is equal to twice the radius(r) =2r
Circles with the same centre but different radii are called concentric circles.
Example: If the radius of the circle is 25 units, find the circumference of the circle. (Take π = 3.14)
Solution: Given, radius = 25 units
Let us write the circumference formula and then we will substitute the value of r (radius) in it.
Circumference of circle formula = 2πr
C = 2 × π × 25
C = 2 × 3.14 × 25 = 157 units
Therefore, the circumference of a circle is 157 units.
Area of Circle
The area of a circle is the region enclosed in the circle. Formulae of area of circle
Formulae of area of circle

where
- r is the radius of the circle
- D is the diameter of the circle
- C is the circumference of the circle
Example 1: The radius of a circular pipe is 10 cm. What length of a tape is required to wrap once around the pipe (π = 3.14)?
Ans: Radius of the pipe (r) = 10 cm
Length of tape required is equal to the circumference of the pipe. Circumference of the pipe = 2πr = 2 × 3.14 × 10 cm = 62.8 cm
Therefore, length of the tape needed to wrap once around the pipe is 62.8 cm.
Example 2: Find the perimeter of the given shape (Take π = 22/7 ).
Ans: In this shape, we need to find the circumference of semicircles on each side of the square.Circumference of the circle = πd
Circumference of the semicircle = 1/2 πd = 1/2 x 22/7 × 14 cm = 22 cm Circumference of each of the semicircles is 22 cm
Therefore, the perimeter of the given figure = 4 × 22 cm = 88 cm.
Example 3: Diameter of a circular garden is 9.8 m. Find its area.
Ans: Diameter, d = 9.8 m
Therefore, radius r = 9.8 ÷ 2 = 4.9 m
Area of the circle = πr2 = 22/7 x (4.9)2 m2 = 22/7 × 4.9 x 4.9 m2= 75.46 m2
Example 4:The adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm. Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
Ans:
(a) Radius of the larger circle = 10 cm So, area of the larger circle = πr2 = 3.14 × 10 × 10 = 314 cm2
(b) Radius of the smaller circle = 4 cm Area of the smaller circle = πr2 = 3.14 × 4 × 4 = 50.24 cm2
(c) Area of the shaded region = (314 – 50.24) cm2 = 263.76 cm2
|
76 videos|344 docs|39 tests
|
FAQs on Perimeter and Area Class 7 Notes Maths Chapter 9
| 1. How do you calculate the area of a parallelogram? |  |
| 2. What is the formula to find the area of a triangle? |  |
| 3. How do you find the circumference of a circle? |  |
| 4. How do you calculate the area of a circle? |  |
| 5. What is the relationship between the area and perimeter of a shape? |  |

|
Explore Courses for Class 7 exam
|

|