Permeability in layered soil - Permeability of Soil, Soil Mechanics | Soil Mechanics Notes- Agricultural Engineering PDF Download
Permeability in layered soil
Figure 17.3 shows a layered soil system. The thickness of each layer is H1, H2, H3 ………. Hn. The coefficient of permeability is k1, k2, k3…………… kn. In case of horizontal flow, it takes place through all the layers at the same time. Thus, hydraulic gradient is same for all the layers, i.e i1 = i2= i3= …… in = i, where n is the number of layers. However, the velocity of flow is different in different layer.
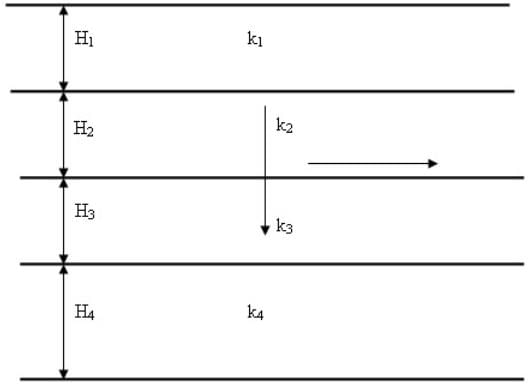
Fig. 17.3. Permeability of layered soil
According to Darcy’s law, the average discharge velocity (vavg) can be written as:
\[{v_{avg}}={k_H}i={1 \over H}({v_1}{H_1} + {v_2}{H_2} + ............. + {v_n}{H_n})\] (17.2)
where kH is the coefficient of horizontal permeability, v1, v2 …….vn is the velocity of flow in different layers. H is the total thickness of the layers, i.e H1+H2+………+Hn = H. The Eq. (17.2) can be written as:
\[{k_H}i={1 \over H}({k_1}i{H_1} + {k_2}i{H_2} + ............. + {k_n}i{H_n})\] (17.3)
\[{k_H}={1 \over H}({k_1}{H_1} + {k_2}{H_2} + ............. + {k_n}{H_n})\] (17.4)
In case of vertical flow, the hydraulic gradient is different in each layer. However, the velocity of flow is same in all the layers. The total head loss ish and the head losses in each layer is h1, h2, ………hn.
Head loss in each layer, \[{h_1}={H_1}{i_1}\] , \[{h_2}={H_2}{i_2}\].......................\[{h_n}={H_n}{i_n}\] (17.5)
Thus, the total head loss \[h={H_1}{i_1} + {H_2}{i_2} + .................. + {H_n}{i_n}\] (17.6)
The velocity of flow is same in all the layers. Thus,
\[v={k_v}{h \over H}={k_1}{i_1}\] (17.7)
where kv is the coefficient of vertical permeability.
Thus,
\[{k_v}={{H{k_1}{i_1}} \over {{H_1}{i_1} + {H_2}{i_2} + ..........{H_n}{i_n}}}\] (17.8)
\[{k_v} = \frac{{H{k_1}{i_1}}}{{\frac{{{H_1}}}{{{k_1}}} + \frac{{{H_2}}}{{{k_2}}} + .......... + \frac{{{H_n}}}{{{k_n}}}}}\] (17.9)
Appendix 17.1
Head loss in each layer, \[{h_1}={H_1}{i_1}\] , \[{h_2}={H_2}{i_2}\]...................\[{h_n}={H_n}{i_n}\] (17.10)
The total head loss \[h={h_1} + {h_2} + .................. + {h_n}\] (17.11)
The velocity of flow is same in all the layers. Thus,
\[v={k_v}{h \over H}={k_1}{{{h_1}} \over {{H_1}}}={k_2}{{{h_2}} \over {{H_2}}}=\cdots={k_i}{{{h_i}}\over {{H_i}}}=\cdots={k_n}{{{h_n}} \over {{H_n}}}\] (17.12)
where kv is the coefficient of vertical permeability. Rearranging,
\[h=v{H \over {{k_v}}}\quad {h_1}=v{{{H_1}}\over{{k_1}}}\quad {h_2}=v{{{H_2}}\over{{k_2}}}\quad\cdots{h_i}=v{{{H_i}}\over{{k_i}}}\quad\cdots{h_n}=v{{{H_n}}\over{{k_n}}}\] (17.13)
The total head loss
\[h=v{H \over{{k_v}}}=v{{{H_1}}\over {{k_1}}}+v{{{H_2}}\over{{k_2}}}+\cdots v{{{H_i}}\over{{k_i}}}+\quad\cdots v{{{H_n}}\over {{k_n}}}\] (17.14)
\[{H \over{{k_v}}}={{{H_1}}\over{{k_1}}}+{{{H_2}}\over {{k_2}}}+\cdots{{{H_i}} \over {{k_i}}}+\quad\cdots{{{H_n}}\over {{k_n}}}\] (17.15)
\[{k_v} = \frac{H}{{\frac{{{H_1}}}{{{k_1}}}+\frac{{{H_2}}}{{{k_2}}}+\cdots\frac{{{H_i}}}{{{k_i}}}+\quad\cdots\frac{{{H_n}}}{{{k_n}}}}}\] (17.16)

|
Explore Courses for Agricultural Engineering exam
|

|
















