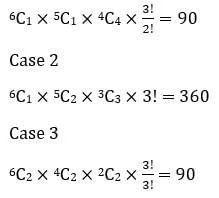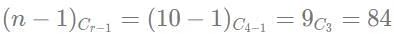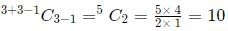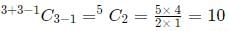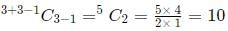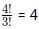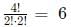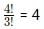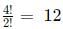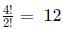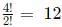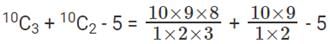Permutation & Combination CAT Previous Year Questions with Answer PDF
2024
Q1: Consider two sets A = {2, 3, 5, 7, 11, 13} and B = {1, 8, 27}. Let f be a function from A to B such that for every element b in B, there is at least one element a in A such that f(a) = b. Then, the total number of such function f is
(a) 667
(b) 540
(c) 665
(d) 537
Ans: b
Sol: Concept: we have to distribute 6 distinct balls into three different boxes:
Case 1 (1, 1, 4)
Hence, the total number of such functions = 90 + 360 + 90<br>
= 540
Q2: P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
Ans: 7
Sol: One can travel from P to S either via PQS or PRS or PQRS= 12 + 4n + 3mn = 62 .
4n + 3mn = 50 -------(1)
One can travel from Q to R either via QR or QPR or QSR = m + 12 + 4n = 27.
m + 4n = 15 -----------(2)
Subtracting equation (2) from equation (1), we get 3mn-m= 35
m(3n - 1) = 35 = 7*5
The number of direct paths between Q and R is m = 7.
2022
Q1: The number of ways of distributing 20 identical balloons among 4 children such that each child gets some balloons but no child gets an odd number of balloons, is
Ans: 84
Sol: Let the number of balloons each child received be 2a, 2b, 2c and 2d
2a + 2b + 2c + 2d = 20
a + b + c + d = 10
Each of them should get more than zero balloons.
Therefore, total number of ways =
Q2: The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
(a) 1200
(b) 1440
(c) 1420
(d) 1480
Ans: b
Sol:
Using 0,1,2,3,4,5 at most once, we have to find number of integers greater than 2000.Case 1: 4-digit numbers
1st digit can take 4 values i.e., 2,3,4,5.
2nd digit can take 6 - 1 = 5 values
3rd and 4th digits can take 4 and 3 values.
Total 4-digit numbers = 4x5x4x3 = 240
Case 2: 5-digit numbers
5x5x4x3x2 = 600
Case 3: 6-digit numbers
5x5x4x3x2x1 = 600
Total = 240+600+600 = 1440
Q3: A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
Ans: 12
Sol:
Let the number of 100, 250, 500 cheques be a, b and c respectively.
100a + 250b + 500c = 15250
=> 2a + 5b + 10c = 305
a + b + c = 100
3b + 8c = 105
3(3) + 8(12) = 105 gives the max value of c i.e., 12.
2021
Q1: The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is [2021]
Ans: 47
Sol: The possible arrangements are of the form
35 _ Can be chosen in 6 ways.
35 _ _ We can choose 2 out of the remaining 6 in 6C2 = 15ways. We remove 1 case where 7 and 8 are together to get 14 ways.
35 _ _ _We can choose 3 out of the remaining 6 in 6C3 = 20ways. We remove 4 cases where 7 and 8 are together to get 16 ways.
35 _ _ _ _We can choose 4 out of the remaining 6 in 6C4 = 15ways. We remove 6 case where 7 and 8 are together to get 9 ways.
35 _ _ _ _ _ We choose 1 out of 7 and 8 and all the remaining others in 2 ways.
Thus, total number of cases = 6 + 14 + 16 + 9 + 2 = 47.
Alternatively,
The arrangement requires a selection of 3 or more numbers while including 3 and 5 and 7, 8 are never included together. We have cases including a selection of only 7, only 8 and neither 7 nor 8.
Considering the cases, only 7 is selected.
We can select a maximum of 7 digit numbers. We must select 3, 5, and 7.
Hence we must have ( 3, 5, 7) for the remaining 4 numbers we have
Each of the numbers can either be selected or not selected and we have 4 numbers :
Hence we have _ _ _ _ and 2 possibilities for each and hence a total of 2 x 2 x 2 x 2
= 16 possibilities.
SImilarly, including only 8, we have 16 more possibilities.
Cases including neither 7 nor 8.
We must have 3 and 5 in the group but there must be no 7 and 8 in the group.
Hence we have 3 5 _ _ _ _.
For the 4 blanks, we can have 2 possibilities for either placing a number or not among 1, 2, 4, 6.
= 16 possibilities
But we must remove the case where neither of the 4 numbers are placed because the number becomes a two-digit number.
Hence 16 - 1 = 15 cases.
Total = 16 + 15 + 16 = 47 possibilities
Q2: The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is [2021]
Ans: 1000
Sol: This question is an application of the product rule in probability and combinatorics.
In the product rule, if two events A and B can occur in x and y ways, and for an event E, both events A and B need to take place, the number of ways that E can occur is xy. This can be expanded to 3 or more events as well.
Event 1: Distribution of balloons
Since each child gets at least 4 balloons, we will initially allocate these 4 balloons to each of them.
So we are left with 15 - 4 x 3 = 15 - 12 = 3 balloons and 3 children.
Now we need to distribute 3 identical balloons to 3 children.
This can be done inways, where n = 3 and r = 3.
So, number of ways =Event 2: Distribution of pencils
Since each child gets at least one pencil, we will allocate 1 pencil to each child. We are now left with 6 - 3 = 3 pencils.
We now need to distribute 3 identical pencils to 3 children
This can be done inways, where n = 3 and r = 3.
So, number of ways =
Event 3: Distribution of erasers
We need to distribute 3 identical erasers to 3 children.
This can be done inways, where n = 3 and r = 3.
So, number of ways =
Applying the product rule, we get the total number of ways = 10 x 10 x 10 = 1000.
Q3: A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is [2021]
Ans: 50
Sol: The question asks for the number of 4 digit numbers using only the digits 1, 2, and 3 such that the digits 2 and 3 appear at least once.
The different possibilities include :
Case 1:The four digits are ( 2, 2, 2, 3). Since the number 2 is repeated 3 times. The total number of arrangements are :
Case 2: The four digits are 2, 2, 3, 3. The total number of four-digit numbers formed using this are :
Case 3: The four digits are 2, 3, 3, 3. The number of possible 4 digit numbers are:
Case4: The four digits are 2, 3, 3, 1. The number of possible 4 digit numbers are :
Case5: Using the digits 2, 2, 3, 1. The number of possible 4 digit numbers are :
Case 6: Using the digits 2, 3, 1, 1. The number of possible 4 digit numbers are :
A total of 12 + 12 + 12 + 4 + 6 + 4 = 50 possibilities.
2018
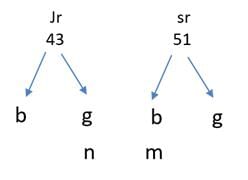
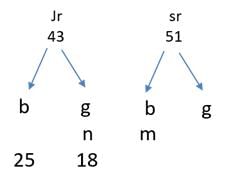
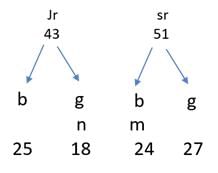
Q1: In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is [2018 TITA]
Ans: 1098
Sol:
Given that in a tournament there are 43 junior level and 51 senior level participants, let us assume that there are n number of girls and m number of boys
The number of girl versus girl matches in junior level is 153
So nC2 = 153
n(n − 1) / 2 = 153
n(n - 1) = 306 = 18 × 17
There are 18 girls and 43 - 18 = 25 boys.
Supposing that m boys in the senior level, mC2 = 276
m(m − 1) / 2 = 276
m(m-1) = 552 = 276 × 2 = 138 × 4 = 69 × 8 = 23 × 24
In senior level there are 24 boys and 27 girls
The number of matches a boy plays against a girl has to be found
⟹ 25 × 18 + 24 × 27
⟹ 450 + 648
⟹ 1098
The number of matches a boy plays against a girl is 1098.
2017
Q1: The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12 is [2017]
(a) 101
(b) 99
(c) 87
(d) 105
Ans: b
Sol: We have to find the number of solutions (x, y, z) to the given equation.
x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12.
x – y – z = 25, so the maximum value y and z can take is 12 and x can take is 40.
From 40 we can subtract some values to get 25 i.e.15 can be subtracted,
If x = 40 then y + z = 15
y ≤ 12 so y can take all the corresponding values 12, 11, 10,......3 it is a set of 10 values.
z ≤ 12, so z can take corresponding other values to get with 15 when added with x
Similarly,
If x = 39, then y + z = 14 here y can take all the value from 12, 11,...till 2
So there are 11 values.
If x = 38, then y + z = 13 here y can take all values from 12, 11, 10,....till 1
So there are 12 values.
If x = 37 then y + z = 12 here y can take 11, 10, 9,.....,1 so there are 11 values
If x = 36 then y + z = 11 here y can take 10, 9,......,1 so there are 10 values
If x = 35 then y + z = 10 here y can take 9, 8,.......,1 so there are 9 values
If x = 34 then y + z = 9 here y can take 8,.......,1 so there are 8 values
If x = 33 then y + z = 8 here y can take 7,........,1 so there are 7values
If x = 32 then y + z = 7 here y can take 6,........,1 so there are 6 values
If x = 31 then y + z = 6 here y can take 5.........,1 so there are 5 values
If x = 30 then y + z = 5 here y can take 4,......,1 so there are 4 values
If x = 29 then y + z = 4 here y can take 3,...,1 so there are 3values
If x = 28 then y + z = 3 here y can take 2,1 so there are 2 values
If x = 27 then y + z = 2 here y can take 1 so there is 1 value
x cannot be less than 27 because it is given that y and z are positive integers so it has to be at least one cannot be less than one
So, 12 × 13 / 2 + 21 = 78 + 21 = 99.
The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12 is 99.
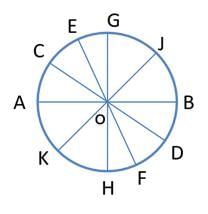
Q2: Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle? [2017 TITA]
Ans: 160
Sol:
Given that AB, CD, EF, GH and JK be five diameters of a circle with center at O.
We have to find by how many ways three points can be chosen out of A, B, C, D, E, F, G, H, J, K and O so as to form a triangle.
We know that any three points lying on the circle are non collinear.
There are 11 points here we have to choose from any three points that are not collinear.
From these 10 points A, B, C, D, E, F, G, H, J, K we can select any three points on the circle such that they are non collinear. We can take O and then from remaining 10 we can take remaining two.
Since AOB , COD , GOH , EOF , JOK cannot form triangles, 5 can be subtracted.
⟹ 120 + 45 – 5 = 160 ways.
Q3: In how many ways can 7 identical erasers be distributed among 4 kids in such a way that each kid gets at least one eraser but nobody gets more than 3 erasers? [2017]
(a) 16
(b) 20
(c) 14
(d) 15
Ans: a
Sol: Given that 7 identical erasers be distributed among 4 kids in such a way that each kid gets at least one eraser but nobody gets more than 3 erasers.
We have to find by how many number of ways the erasers are distributed such that each kid gets at least one eraser but no body gets more than 3 erasers.
Let us assume the 4 kids to be a, b, c, d such that a + b + c + d = 7.
It can be distributed in 6C3 ways
⟹ 6 × 5 × 4 / 3 × 2 × 1 = 20
It is given that no body gets more than 3 erasers so let us say that one kid could get 4, 5, 6 eraser.
If one kid a, gets 4 erasers the other kids b, c, d can get each one respectively such that 4, 1, 1, 1 or 1, 1, 1, 4 or 1, 4, 1, 1 or 1, 1, 4, 1 so there are chances of 4 ways.
So, 20 – 4 = 16 ways
Q4: In how many ways can 8 identical pens be distributed among Amal, Bimal, and Kamal so that Amal gets at least 1 pen, Bimal gets at least 2 pens, and Kamal gets at least 3 pens? [2017 TITA]
Ans: 6
Sol: Let us assume Amal gets 1 + x pens and Bimal gets 2 + y pens and Kamal gets 3 + z pens
1 + x + 2 + y + 3 + z = 8
x + y + z = 2 (x, y, z being whole numbers) or
x + (1 + y) + (3 + z )
x + y + z = 8 – 3 = 5 (x, y, z being naturals numbers)
Take 5 ones 1 _ 1 _ 1 _ 1 _ 1 , + symbol should be added in any 2 slots. (There are 4 empty slots)
This is done in 4C2 ways = 6 ways.
Alternative method is to list down the possibilities as done below.
Q5: How many four digit numbers, which are divisible by 6, can be formed using the digits 0, 2, 3, 4, 6, such that no digit is used more than once and 0 does not occur in the left-most position? [2017 TITA]
Ans: 50
Sol: We have to find the no. of four digit numbers which are divisible by 6 that are to be formed using the digits 0, 2, 3, 4, 6.
We should know that 0 does not occur in the left most position. If the numbers are to be divisible by 6 it should be a multiple of 2 and 3.
So it should be an even number and also should be a multiple of 3.
⟹ 2 + 3 + 4 + 6 + 0 = 15
Here we have two choices, drop something such that the number should be a multiple of 3 or we can drop a multiple of 3.
The following are the possibilities,
Drop 3 ⟹ 2 + 4 + 6 + 0 = 12 which is a multiple of 3.
Drop 6 ⟹ 2 + 3 + 4 + 0 = 9 which is a multiple of 3.
Drop 0 ⟹ 2 + 3 + 4 + 6 = 15 which is a multiple of 3.
We have to check the possible outcomes,
For 2 , 4 , 6 , 0 ⟹ 3 × 3 × 2 × 1 = 18 ways.
For 2 , 3 , 4 , 0 ⟹ 3 × 3 × 2 × 1 = 18 ways.
But out of these 18 outcomes there will be some possibilities where the last digit is 3.
4 such possibilities exist here which needs to be eliminated.
Therefore 18 – 4 = 14 ways.
For 2, 3, 4 and 6 if we have last digit as 3 ie. _ _ _ 3, we can rearrange 2, 4 and 6 in 3! ways
Hence 2, 3, 4 and 6 can be arranged in 4! - 3! = 24 – 6 = 18 ways.
Therefore, in total we can form 18 + 14 + 18 = 50 four digit numbers.
|
174 videos|243 docs|95 tests
|
FAQs on Permutation & Combination CAT Previous Year Questions with Answer PDF
| 1. What is the difference between permutation and combination in CAT exams? |  |
| 2. How can I solve permutation and combination problems effectively in CAT exams? |  |
| 3. Can you provide an example of a permutation problem in CAT exams? |  |
| 4. How do I approach combination problems in CAT exams? |  |
| 5. Can you provide an example of a combination problem in CAT exams? |  |