Question with Answers: Pipes and Cistern - 2 | Quantitative Aptitude (Quant) - CAT PDF Download
Question 11: Pipe A can fill a tank in 12 hours. When it works along with Pipe B, it can fill the tank in 8 hours. In how many hours can pipe B fill the same tank independently?
(A) 8 hrs
(B) 12 hrs
(C) 24 hrs
(D) 16 hrs
Answer: C
Explanation:
Let the capacity of the tank be C.
Rate of Pipe A = C/A
Rate of Pipe B = C/B
Rate of Pipe A and Pipe B together = C/A + C/B = C/8
C/12 + C/B = C/8
C/B = C/8 - C/12 = C/24
Pipe B independently will take 24 hours to fill the tank.
The question is "In how many hours can pipe B fill the same tank independently?"
Hence, the answer is "24 hrs"
Question 12: Number of units of a good that can be produced by a factory is directly proportional to the square of the number of workers, square root of the number of machines and to the number of hours put in. The factory produces 200 goods when 4 people work for 8 hours each with 4 machines. When 3 people work for 12 hours each with 9 machines, how many goods will be produced?
(A) K = 253.125
(B) K = 100/163
(C) K = 25/256
(D) K = 16/29
Answer: A
Explanation:
G α No of workers2
G α √(No. of Machines)
G α No of hours
200 α 42 * √4 * 8
200 α 16 * 2 * 8
200 α 256
200 = k x 256
K = 200/256
K = 25/32
When 3 people work for 12 hours each with 9 machines, the number of goods that will be produced is equal to 25/32 * 32 * √9 * 12 = 253.125
The question is "When 3 people work for 12 hours each with 9 machines, how many goods will be produced?"
Hence, the answer is "K = 253.125".
Question 13: A can complete a task in 12 days. B can complete the task in 18 days. If A and B work on this same task in alternate days starting with A, in how many days do they finish the entire task?
(A) 10.8 days
(B) 14.33 days
(C) 11 days
(D) 8.4 days
Answer: B
Explanation:
A can complete a task in 12 days and B can complete the task in 18 days. So,
In one day, A can do 1/12, in one day B can do 1/18.
In two days, they can complete 1/12 + 1/18 = which is 5/36.
In 4 days, they can finish 10/36, and so on.
We can have 7 such sets of 2days each.
So, at the end of 14 days, they would have done 35/36 of task.
On the 15th day A would begin work with 1/36of the task to finish. He can finish 1/12 in a day. So, he would take one-third of a day. So, they can finish the whole task in 14.33 days.
The question is "how many days do they finish the entire task?"
Hence, the answer is "14.33 days".
Question 14: A can complete a task 4 hours lesser time than B takes to complete the same. If A and B together can complete the task in 288 minutes, how long does B alone take to complete the task?
(A) 1 hr
(B) 2 hrs
(C) 3 hrs
(D) 12 hrs
Answer: D
Explanation:
Let time taken by A be 'a' hours and time taken by B be 'a+4' hours
Then A does 1/a of the work in an hour.
B does 1/a+4 of the work in an hour.
Together they take 288 minutes to finish the job , 288 minutes = 288/60 = 24/5 hours.
Therefore, both A and B together complete 5/24 every hour.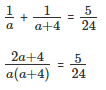
We get, 48a + 96 = 5(a2 + 4a
=> 5a2 - 28a - 96 = 0
=> 5a2 - 40a + 12a - 96 = 0
5a (a - 8) + 12(a - 8) = 0
(5a + 12)(a - 8) = 0 . Therefore, Since a cannot be negative, a = 8 hours.
Hence, a + 4 = 12 hours. Therefore, Time taken by B to complete the work on his own is 12 hours. The question is "how long does B alone take to complete the task?"
Hence, the answer is "12 hrs".
Question 15: A Two pipes can fill a tank in 12 hrs and 18 hrs respectively. The pipes are opened together but due to a pipe leakage , it takes 48 minutes extra to fill the tank, If the tank is full, what time will it take to completely empty due to the leakage.
(A) 72 hrs
(B) 84 hrs
(C) 96 hrs
(D) 112 hrs
Answer: A
Explanation:
Time taken to fill the tank completely without leakage = 1/(1/12)+(1/18) hrs
= 1/(9+6)/108 = 108/15 = 7 hours and 12 minutes
Given, it takes 48 minutes extra with the leakage. So, total time taken = 8 hours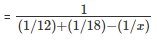 = 8 (Where, x is the time taken by the leakage to completely empty the tank)
= 8 (Where, x is the time taken by the leakage to completely empty the tank)
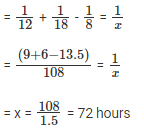
The question is "what time will it take to completely empty due to the leakage."
Hence, the answer is "72 hrs".}
Question 16: A cistern of capacity 40 litres has an inlet and an outlet pipe. When both the pipes are opened at once, it takes 8 minutes to fill the cistern. However, if the outflow rate is increased 1.5 times, the cistern never gets filled. Which of the following can be the outflow rate?
(A) 8 litres/minute
(B) 6 litres/minute
(C) 12 litres/minute
(D) 9 litres/minute
Answer: C
Explanation:
Initially, net flow in the tank = 40 litres/ 8 minutes = 5 litres/minute
Now, the increase in outflow should be greater than 5 litres/min for the tank to fill up.
Increase in outflow = 1.5x – x = 0.5x
Only in option C, 0.5 * 12 = 6 litres/min > 5 litres/min
The question is "Which of the following can be the outflow rate?"
Hence, the answer is "12 litres/minute".
Question 17: A cistern of 475 litres is completely filled using pipes A and B, with Pipe A being open for 5 more hours than pipe B. If we are to interchange the operating hours of the two pipes than pipe A would have pumped half the water as much as pipe B, then find the time for which pipe B was open. Also, given that if the two pipes were open simultaneously the tank would fill in 19 hours.
(A) 10 hrs
(B) 14 hrs
(C) 16 hrs
(D) 20 hrs
Answer: C
Explanation:
The 475 litres is filled in 19 hours by the two pipes when they are opened simultaneously.
Therefore, rate of water flow by A and B,
A + B = 475/19 = 25 litres/hour………….(1)
Let pipe B was opened for t hours
Then, pipe A was opened for t + 5 hours
A x (t+5) + B x t = 475
(A + B) x t + 5A = 475
25t + 5A = 475
=> 5t + A = 95
Now, using option analysis
a) t = 10 => 5 x 10 + A = 95 => A = 45 (not possible from (1))
b) t = 14 => 5 x 14 + A = 95 => A = 25 (not possible from (1) as B can’t be zero)
c) t = 16 => 5 x 16 + A = 95 => A = 15
The question is "if the two pipes were open simultaneously the tank would fill in 19 hours."
Hence, the answer is "16 hrs".
Question 18: A mining team made a plan to mine up to 300 m in a certain number of days. After working as per plan for 5 days, they added new members to the team and hence could mine 5 m more per day. In this way, 4 days before the planned date, they had mined 295 m. How many meters of mining was initially planned for each day?
(A) 30 m
(B) 12.5 m
(C) 15 m
(D) 7.5 m
Answer: C
Explanation:
Given, 295 m was mined out of which first 5 days – planned. Using option analysis:
a) 30 * 5 + (30 + 5) * (300/30 – 5 – 4) = 150 + 35 * 1 = 185 ≠ 295
b) 12.5 * 5 + 17.5 * (300/12.5 – 5 – 4) = 62.5 + 17.5 * 15 = 325 ≠ 295
c) 15 * 5 + 20 * (300/15 – 5 – 4)1 = 75 + 20 * 11 = 295
The question is "How many meters of mining was initially planned for each day?"
Hence, the answer is "15 m".
Question 19: Ajay and Suraj can water a garden in 45 minutes and 40 minutes respectively. They started working together but after some time Ajay left to watch a cricket match. Suraj hurriedly finished the work in next 23 minutes and joined Ajay. After how many minutes had Ajay left?
(A) 9 min
(B) 8 min
(C) 7 min
(D) 10 min
Answer: A
Explanation:
Suraj took 23 minutes to finish the remaining work = 23/40
Work finished by Ajay and Suraj together = 17/40
Time taken = 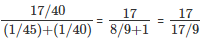 = 9 mins
= 9 mins
The question is "how many minutes had Ajay left?"
Hence, the answer is "9 min".
Question 20: Bibhor takes 3 hours to fetch as much water as Ahmed can fetch in 2 hours. Deepak takes 5 hours to fetch as much water as Bibhor can fetch in 4 hours. A tank takes 20 hours to fill if all work together. What time would Bibhor take to fill the tank alone?
(A) 50 hrs
(B) 56 hrs
(C) 77 hrs
(D) 66 hrs
Answer: D
Explanation:
Let the work done by Ahmed be 60 (LCM of 2,3,4,5)
So, work done per hour by:
Ahmed – 60/2 = 30
Bibhor – 60/3 = 20
Bibhor in 4 hours – 20 x 4 = 80
Deepak – 80/5 = 16
Therefore, total work done in an hour = 30 + 20 + 16 = 66
If all 3 work for 20 hours, total work done = 66 * 20
If Bibhor alone has to work, time taken to do 66 * 20 of work = 66 * 20/20 (work done by Bibhor in 1 hour)
= 66 hours
The question is "What time would Bibhor take to fill the tank alone?"
Hence, the answer is "66 hrs".
|
167 videos|229 docs|95 tests
|
FAQs on Question with Answers: Pipes and Cistern - 2 - Quantitative Aptitude (Quant) - CAT
| 1. What is the formula to calculate the time taken to fill a cistern with a pipe? |  |
| 2. How can one calculate the efficiency of a pipe filling a cistern? |  |
| 3. Can two pipes working together fill a cistern faster than a single pipe alone? |  |
| 4. How can one determine the time taken for two pipes working together to fill a cistern? |  |
| 5. What should be done if a leakage in the cistern is given along with the filling pipes in a problem? |  |

















