Pipes and Cisterns - Concepts and Tricks | IBPS PO Prelims & Mains Preparation - Bank Exams PDF Download
Introduction
Competitive exams consistently feature questions on pipes and cisterns. Typically, problem-solving in this category involves applying methods related to work and time. These questions are often presented as word problems during competitive examinations, employing concepts akin to those used in work and time problems.
The basic structure of these types of questions is,
- A tank has to be filled or emptied by two or more pipes
- Time taken by each pipe to fill or empty the tank is given or should be found
- Total time taken to fill or empty the tank is given or should be found
Pipes
Pipes are conduits linked to tanks for either filling or draining liquids. Tanks, alternatively termed cisterns or reservoirs, are the containers in question. Consequently, the inquiries revolve around the effectiveness of pipes in the processes of tank filling or emptying.
There are two types of pipes:
Inlet Pipe: As the name implies, these pipes are employed to introduce or deliver liquid into the tank. In simpler terms, inlet pipes facilitate the filling of tanks.
Outlet Pipe: As the name implies, these pipes are utilized to discharge or expel liquid from the tank. In simpler terms, outlet pipes facilitate the emptying of tanks. They may also be referred to as leaks.

Formulae and Short Tricks
Here are some formulas and brief techniques for solving problems related to pipes and cisterns:
Formula 1:
If pipe A can completely fill a tank in x hours, then the portion filled in 1 hour is . (or) If pipe A fills 1/x portion of the tank in 1 hour, then the time taken by the pipe to fill the full tank is x hours.
Example: If a pipe fully fills a tank in 10 hours, what part of the tank will be filled by the pipe in 1 hour?
Sol: According to the above given formula, if pipe can comletely fill a tank in x hours, then the portion filled in 1 hour is 1/x
Hence, 1/10th part of the tank will be filled by the pipe in 1 hour.
Formula 2:
If pipe A can completely empty a tank in y hours, then the portion emptied in 1 hour is 1/y (or) If pipe A empties 1/y portion of the tank in 1 hour, then the time taken by the pipe to empty the full tank is y hours.
Example: If an outlet pipe can empty a cistern in 15 hours, in what what time can the pipe empty 3/5 of the cistern?
Sol: According to the above given formula, if pipe can comletely empty a tank in y hours, then the portion emptied in 1 hour is 1/y
so, 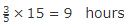 Hence, 3/5 th part of the tank will be emptied by the pipe in 9 hours.
Hence, 3/5 th part of the tank will be emptied by the pipe in 9 hours.
Formula 3:
If pipe A fills a tank in x hours and another pipe B fills a tank in y hours, then the time taken by both pipes together to fill the tank is  hours.
hours.
Example: If a pipe can fill a tank in 2 hours and another pipe can fill the same tank in 8 hours, then what part of the tank can be filled by both the pipes when opened simultaneously?
Sol: According to the above given formula, if pipe A can comletely fill a tank in x hours and pipe B can comletely fill a tank in y hours, then the time taken by both pipes together to fill the tank is 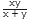 hours.
hours.
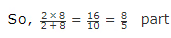 Hence, 8/5th part of the tank will be filled by both the pipe when opened simultaneously.
Hence, 8/5th part of the tank will be filled by both the pipe when opened simultaneously.
 |
Pipes And Cistern - MCQ 1
|
Start Test |
Formula 4:
If pipe A fills a tank in x hours and another pipe B empties the tank in y hours (where y>x), then the time taken to fill the tank when both the pipes are open is 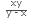 hours.
hours.
Example: If a pipe can fill a tank in 5 hours and another pipe can empty the same tank in 7 hours. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?
Sol: According to the above given formula, if pipe A can comletely fill a tank in x hours and pipe B can empty the same tank in y hours, then the time taken to fill the tank when both the pipes are opened simultaneously is 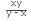 hours.
hours.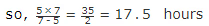 Hence, the tank will be filled in 17.5 hours when both the pipes are opened simultaneously.
Hence, the tank will be filled in 17.5 hours when both the pipes are opened simultaneously.
Formula 5:
If pipe A fills a tank in x hours and another pipe B empties the tank in y hours (where x>y), then the time taken to fill the tank when both the pipes are open is 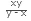 hours.
hours.
Example: If a pipe can fill a tank in 15 hours and another pipe can empty the same tank in 8 hours. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?
Sol: According to the above given formula, if pipe A can comletely fill a tank in x hours and pipe B can empty the same tank in y hours, then the time taken to fill the tank when both the pipes are opened simultaneously is 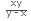 hours.
hours. Hence, the tank will be filled in 17.14 hours when both the pipes are opened simultaneously.
Hence, the tank will be filled in 17.14 hours when both the pipes are opened simultaneously.
Formula 6:
If three pipes A, B and C can fill the tank separately in x hours, y hours and z hours respectively then, the time taken by all the three pipes together to fill the tank is 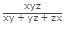 hours.
hours.
Example: Three pipes x, y, z fill a tank in 4, 5, and 6 hours respectively. The time taken by all the three pipes to fill the tank when opened simultaneously is?
Sol: According to the above given formula, If three pipes A, B and C can fill the tank separately in x hours, y hours and z hours respectively then, the time taken by all the three pipes together to fill the tank is 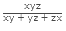 hours.So,
hours.So, Hence, the tank will be filled in
Hence, the tank will be filled in 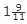 hours when all the pipes are opened simultaneously.
hours when all the pipes are opened simultaneously.
Formula 7:
If pipe A and B fills a tank in x and y hours respectively, but a third pipe C empties the full tank in z hours then the net portion filled in 1 hour when all of them are opened together is 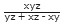 hours.
hours.
Example: Two pipes x, y fill a tank in 20, 10 hours respectively. The third pipe z empties the full tank in 30 hours. If all the three are opened simultaneously, how much time will be required to fill the tank?
Sol: According to the above given formula, If pipe A and B fills a tank in x and y hours respectively, but a third pipe C empties the full tank in z hours then the net portion filled in 1 hour when all of them are opened together is 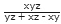 hours.So,
hours.So, 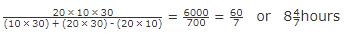 Hence, the tank will be filled in
Hence, the tank will be filled in 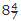 hours when all the pipes are opened simultaneously.
hours when all the pipes are opened simultaneously.
Formula 8:
Two pipes A and B can fill the tank in x and y min respectively. If both pipes are opened together, then the time after which pipe B should be closed so that the tank is full in t min is 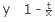 min.
min.
Example: Two pipes m and n can fill a tank in 12, 6 min respectively. If both the pipes are opened simultaneously, after how much time should pipe n be closed so that the tank is full in 4 min?
Sol: According to the above given formula, If Two pipes A and B can fill the tank in x and y min respectively. If both pipes are opened together, then the time after which pipe B should be closed so that the tank is full in t min is 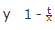 min.
min.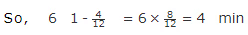
Hence, the tank will be filled in 4 min both the pipes are opened simultaneously.
 |
Download the notes
Pipes and Cisterns - Concepts and Tricks
|
Download as PDF |
Formula 9:
Two pipes A and B can together fill a tank in time T. If time taken by pipe A alone is more than T by x and the time taken by pipe B alone is more than T by y, then T is
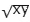 min.
min.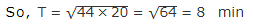 Hence, the tank will be completely filled in 8 min.
Hence, the tank will be completely filled in 8 min.
Formula 10:
Suppose we have many pipes, where some fill the tank and some empty the tank. If we open all of them together, then in one hour,
- the part of the tank filled is ∑ (1 / xi) + ∑ (1 / yo)
- the part of the tank emptied is ∑ (1 / xi) - ∑ (1 / yo)
where ‘xi‘ is the time taken by inlet pipe ‘i’ to fill the tank completely if only it was open and ‘yo‘ is the time taken by outlet pipe ‘o’ to empty the tank completely if only it was open.
|
541 videos|681 docs|263 tests
|
FAQs on Pipes and Cisterns - Concepts and Tricks - IBPS PO Prelims & Mains Preparation - Bank Exams
| 1. What are the basic concepts of pipes and cisterns? |  |
| 2. How do you solve problems related to pipes and cisterns in banking exams? |  |
| 3. What are the common tricks or shortcuts to solve pipes and cisterns problems quickly? |  |
| 4. Can you provide an example problem related to pipes and cisterns? |  |
| 5. How can I improve my speed and accuracy in solving pipes and cisterns problems for banking exams? |  |






















