Playing with Numbers Class 6 Notes Maths
Introduction
Numbers are a big part of math, and knowing how they work is important for solving everyday problems. By learning about things like factors, multiples, and divisibility rules, you can better understand how numbers are connected. You will also learn about prime and composite numbers, and how to find the highest common factor (HCF) and least common multiple (LCM). These ideas help you see the patterns in numbers, making math both useful and enjoyable.
Factors and Multiples
(i) Factors
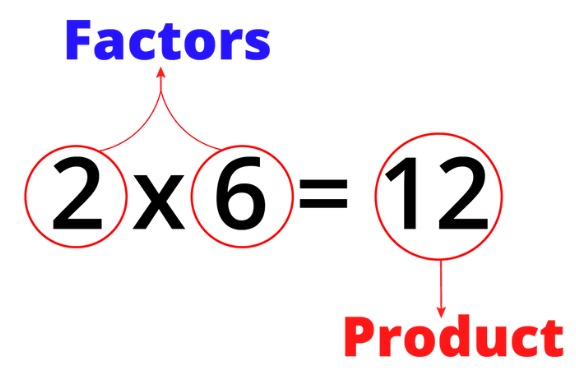
A factor of a number is a whole number that divides exactly into that number, leaving no remainder. Factors come in pairs, and each pair multiplies together to give the original number.
Examples:
Factors of 12:
1 x 12 = 1 and 12: 12 ÷ 1 = 12, so 1 and 12 are factors of 12.
2 x 6= 2 and 6: 12 ÷ 2 = 6, so 2 and 6 are factors of 12.
3 x 4 = 3 and 4: 12 ÷ 3 = 4, so 3 and 4 are factors of 12.
All factors of 12 are: 1, 2, 3, 4, 6, and 12.
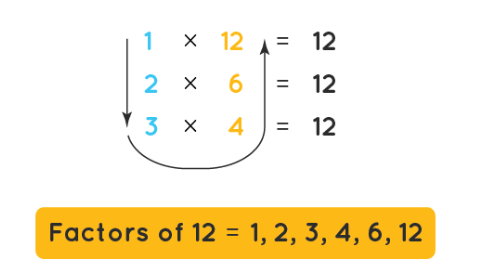
Factors of 15:
1 x 15 = 1 and 15: 15 ÷ 1 = 15, so 1 and 15 are factors of 15.
3 x 5 = 3 and 5: 15 ÷ 3 = 5, so 3 and 5 are factors of 15.
All factors of 15 are 1, 3, 5, and 15.
Factors of 20:
1 x 20 = 1 and 20: 20 ÷ 1 = 20, so 1 and 20 are factors of 20.
2 x 10 = 2 and 10: 20 ÷ 2 = 10, so 2 and 10 are factors of 20.
4 x 5 = 4 and 5: 20 ÷ 4 = 5, so 4 and 5 are factors of 20.
All factors of 20 are 1, 2, 4, 5, 10, and 20.
Properties of Factors
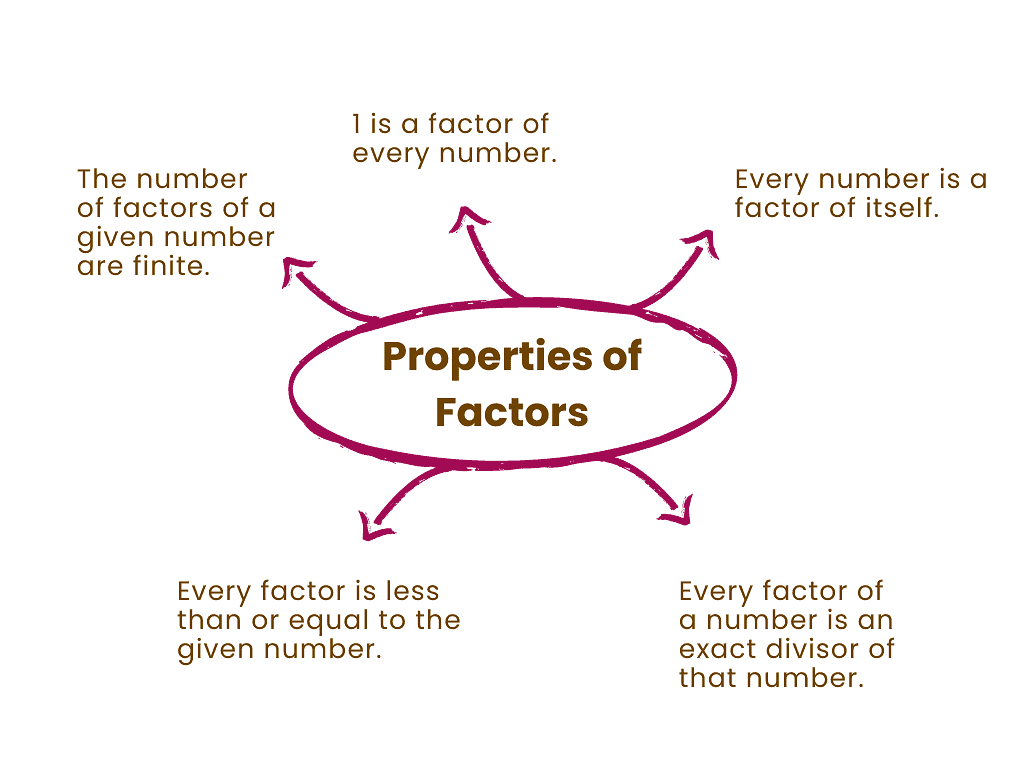
1. 1 is a factor of every number:
For example:
1 is a factor of 6 (because 6 = 1 × 6).
1 is a factor of 18 (because 18 = 1 × 18).
2. Every number is a factor of itself:
For instance:
7 is a factor of 7 (because 7 = 7 × 1).
10 is a factor of 10 (because 10 = 10 × 1).
15 is a factor of 15 (because 15 = 15 × 1).
3. Every factor of a number divides that number exactly:
For example:
The factors of 16 are 1, 2, 4, 8, and 16. Each divides 16 exactly:
16 ÷ 1 = 16
16 ÷ 2 = 8
16 ÷ 4 = 4
16 ÷ 8 = 2
16 ÷ 16 = 1
4. Every factor of a number is less than or equal to that number:
For example, the factors of 34 are 1, 2, 17, and 34. All these factors are less than or equal to 34.
5. A number has a finite number of factors:
For instance, 76 has 5 factors. Even large numbers like 10576 or 25642 have a limited number of factors, though finding them might be more complex.
(ii) Multiples
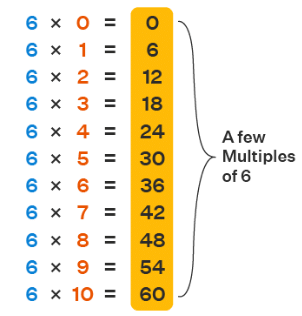
Multiples of a number are the results you get when you multiply that number by any whole number. In simple terms, multiples are the numbers you get in a sequence by repeatedly adding the original number.
Example:

Properties of Multiples
1. Every number is a multiple of 1:
For example, 7 × 1 = 7, and 9 × 1 = 9. So, every number is a multiple of 1.
2. Every number is a multiple of itself:
For example, 7 × 1 = 7 and 21 × 1 = 21. Every number is a multiple of itself.
3. Zero (0) is a multiple of every number:
For example, 0 × 9 = 0, and 0 × 11 = 0. Zero is a multiple of any number.
4. Every multiple except zero is either equal to or greater than any of its factors:
For example, multiples of 7 include 7, 14, 21, and 28. All these multiples are greater than or equal to 7, which is a factor.
5. The product of two or more factors is a multiple of each factor:
For example, 3 × 7 = 21, so 21 is a multiple of both 3 and 7. Similarly, 30 = 2 × 3 × 5, so 30 is a multiple of 2, 3, and 5.
6. There is no end to the multiples of a number:
For example, multiples of 5 are 5, 10, 15, 20, 25, and continue indefinitely.
Understand more about the properties of Factors and Multiples through this video:
(iii) Perfect Numbers
A perfect number is a positive integer that is equal to the sum of its factors except for the number itself. In other words, perfect numbers are the positive integers that are the sum of its divisors.

Example: The smallest perfect number is 6, which is the sum of its factors: 1, 2, and 3. It is to be noted that this sum does not include the number itself which is also a factor of itself.
We can look at another perfect number, 28: The proper divisors are 1, 2, 4, 7, and 14. Their sum is 1 + 2 + 4 + 7 + 14 = 28.
Here are some more examples of Perfect Numbers:
 Examples of Perfect Numbers
Examples of Perfect Numbers
Lets us look into some solved example problems of Factors, Perfect Numbers and Multiples:
Q1: List the first 5 multiples of 5, 8 and 9.
Ans: First 5 multiples of 5 are : 10, 15, 20, 25, 30
First 5 multiples of 8 are : 8, 16, 24, 32, 40
First 5 multiples of 9 are: 9, 18, 27, 36, 45
Q2: Which number is a factor of 10 among the numbers 3,4,5 & 8?
Ans: 5 is a factor of 10 among the numbers 3,4,5 & 8. If you can multiply two whole numbers to create a third number, those two numbers are factors of the third. 2 x 5 = 10, so 2 and 5 are factors of 10
Q3: Write all the factors of the following numbers: (a) 24 (b) 15 (c) 21
Ans: (a) Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
(b) Factors of 15: 1, 3, 5, 15
(c) Factors of 21: 1, 3, 7, 21
Q4: Find all the multiples of 9 upto 100.
Ans: Here are the multiples of 9 up to 100:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99
Q5: Write all the factors of 68.
Ans: We note that:
68 = 1 × 68
68 = 2 × 34
68 = 4 × 17
68 = 17 × 4
Stop here, because 4 and 17 have occurred earlier. Thus, all the factors of 68 are 1, 2, 4, 17, 34 and 68
Prime and Composite Numbers
(i) Prime Numbers
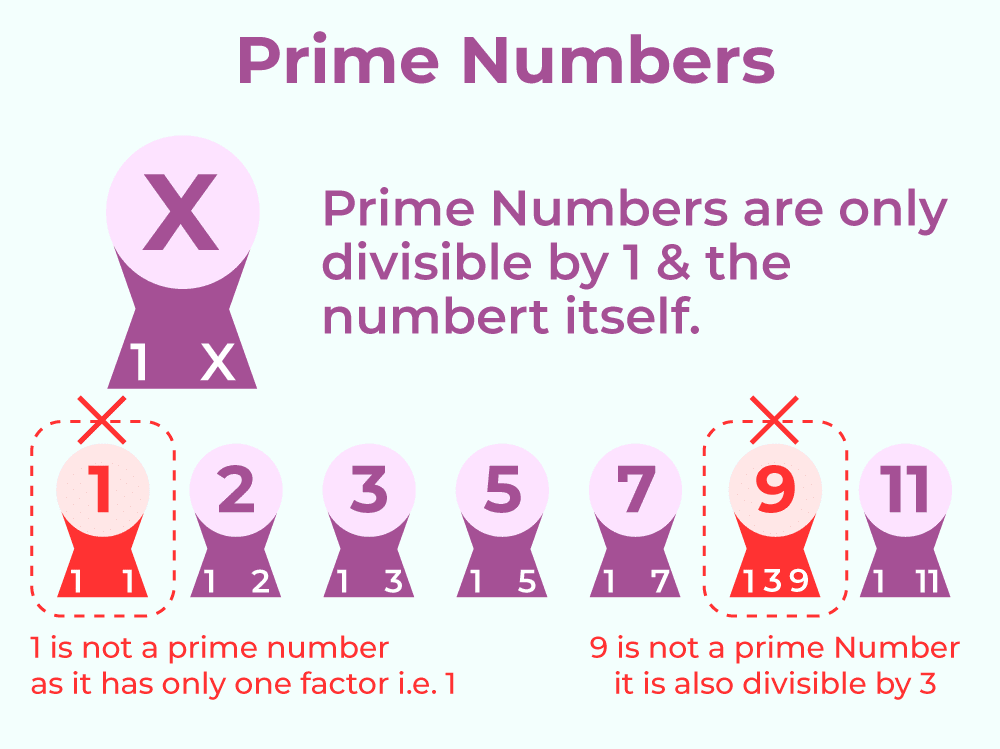
A prime number is a number greater than 1 that has exactly two factors: 1 and itself.
Examples:
2: Its factors are 1 and 2.
3: Its factors are 1 and 3.
5: Its factors are 1 and 5.
Prime numbers only have two factors and cannot be divided evenly by any other numbers except 1 and themselves.
Look at the prime numbers:

Properties of Prime Numbers
Some of the important properties of prime numbers are given below:
- A prime number is a whole number greater than 1.
- It has exactly two factors, that is, 1 and the number itself.
- There is only one even prime number, that is, 2.
- Any two prime numbers are always co-prime to each other.
- Every number can be expressed as the product of prime numbers.
(ii) Composite Numbers
A composite number is a number greater than 1 that has more than two factors.
Composite numbers can be divided evenly by numbers other than just 1 and themselves.
Example:
4: Its factors are 1, 2, and 4.
6: Its factors are 1, 2, 3, and 6.
9: Its factors are 1, 3, and 9.
Properties of Composite Numbers
- Composite numbers have more than two factors.
- They can be divided by numbers other than 1 and themselves.
- Can be expressed as a product of prime numbers.
- They are always greater than 1.
- They are not prime because they have more than two factors.
- They have divisors other than 1 and themselves.
- Multiples of Smaller Factors: They are multiples of smaller numbers.
1 is neither prime nor composite: It only has one factor (itself), so it does not fit into either category.
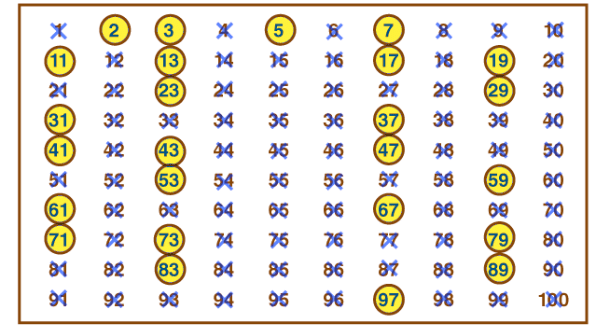
Finding Prime Numbers Using the Sieve of Eratosthenes:
- List numbers from 1 to 100.
- Cross out 1 (not a prime).
- Circle 2 and cross out all its multiples (4, 6, 8, etc.).
- Circle the next uncrossed number (3) and cross out all its multiples (6, 9, 12, etc.).
- Continue with the next uncrossed number (5), and so on.
- The numbers that remain circled are prime.
- Example: To find primes less than 15, you will circle 2, 3, 5, 7, 11, and 13.
Even Numbers: Numbers that can be divided by 2 with no remainder, ending in 0, 2, 4, 6, or 8.
Odd Numbers: Numbers that cannot be evenly divided by 2, ending in 1, 3, 5, 7, or 9.
Special Note: 2 is the only even prime number. All other prime numbers are odd.
Lets us look into some solved example problems of Prime and Composite Numbers:
Q1: Write all the prime numbers less than 15
Ans: Prime numbers are numbers greater than 1 that have no positive divisors other than 1 and itself. Here are the prime numbers less than 15: 2, 3, 5, 7, 11, 13
Q2: Express the following as the sum of two odd primes.
(a) 44 (b) 36 (c) 24 (d) 18
(a) 44: 13 + 31 = 44 (both 13 and 31 are odd primes)
(b) 36: 17 + 19 = 36 (both 17 and 19 are odd primes)
(c) 24: 5 + 19 = 24 (both 5 and 19 are odd primes)
(d) 18: There is no combination of two odd prime numbers that adds up to 18.
So, for (a), (b), and (c), we can express them as the sum of two odd primes, but for (d), it is not possible.
Q3: Write down separately the prime and composite numbers less than 20
Ans: Here are the prime numbers and composite numbers less than 20:
Prime Numbers:
2, 3, 5, 7, 11, 13, 17, 19
Composite Numbers:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18
Tests for Divisibility of Numbers
A divisibility rule is a method of determining whether a given integer is divisible by a fixed divisor without performing division, usually by examining its digits.
Divisibility test for 2
The divisibility rule for 2 states that any number with the last digit of 0, 2, 4, 6, or 8 will be divisible by 2.Simply put, any even number (numbers that end in 0, 2, 4, 6, or 8) is divisible by 2.
 Example: 2580, 4564, 90032 etc. are divisible by 2.
Example: 2580, 4564, 90032 etc. are divisible by 2.
Divisibility test for 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
 Example:
Example:
90453 (9 + 0 + 4 +5 + 3 = 21)
21 is divisible by 3. 21 = 3 × 7. Therefore, 90453 is also divisible by 3.
Divisibility test for 4
A number with 3 or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
Example:
456832960, here the last two digits are 60 that are divisible by 4 i.e.15 × 4 = 60. Therefore, the total number is divisible by 4.
Divisibility test for 5
A number is divisible by five if the last digit of that number is either 0 or 5.
 Example:
Example:
Divisibility test for 6
If a number is divisible by 2 and 3 both, then it is divisible by 6 also.
 Example:
Example:
10008, has 8 at one’s place so is divisible by 2 and the sum of 1, 0, 0, 0 and 8 gives the total 9 which is divisible by 3.
Therefore, 10008 is divisible by 6.
Example: Use the divisibility test to determine whether the number 1258 is divisible by 6.
Ans: Given number is 1258.
Its units digit is 8, which is divisible by 2. So, 1258 is divisible by 2.
Sum of its digits = 1 + 2 + 5 + 8 = 16, which is not divisible by 3. So, 1258 is not divisible by 3.
Since 1258 is divisible by 2 but not by 3, it is not divisible by 6.
Divisibility test for 8
A number with 4 or more digits is divisible by 8, if the number formed by its last three digits is divisible by 8.
 Example:
Example: 
Divisibility test for 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
 Example:
Example: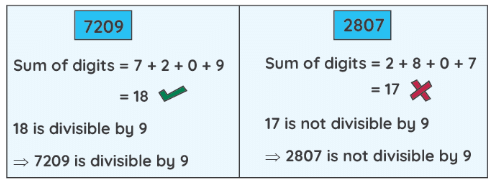
Divisibility test for 10
A number is divisible by 10 if it has only 0 as its last digit. A number that is divisible by 10 is divisible by 5, but a number that is divisible by 5 may or may not be divisible by 10.
10 is divisible by both 5 and 10, but 55 is divisible only by 5, not by 10.
 Example: 89540, 3456780, 934260, etc are all divisible by 10.
Example: 89540, 3456780, 934260, etc are all divisible by 10.
Divisibility test for 11
Find difference between sum of digits at odd places (from the right) and sum of digits at even places (from the right) of a number. If the difference is either 0 or divisible by 11, then the number is divisible by 11.
 Example: 1234321 is divisible by 11 since, (1+3+3+1) – (2+4+2) = 8 – 8 = 0, which is divisible by 11.
Example: 1234321 is divisible by 11 since, (1+3+3+1) – (2+4+2) = 8 – 8 = 0, which is divisible by 11.
Common Factors and Common Multiples
(i) Common Factors
Factors that are common to two or more numbers are known as their common factors.
- The factors of 4 are 1, 2, and 4.
- The factors of 18 are 1, 2, 3, 6, 9, and 18.
- The numbers 1 and 2 are common factors of both 4 and 18.

(ii) Common Multiples
Multiples that are common to two numbers are known as common multiples of those numbers. Let us understand with the help of an example.
- Multiples of 3 are 3, 6, 9, 12, 15, 18,….
- Multiples of 5 are 5, 10, 15, 20, 25, 30,…
- Multiples of 6 are 6, 12, 18, 24, 30, 36,…
Therefore, common multiples of 3, 5, and 6 are 30, 60,….
Example 1: Find the common factors of 75, 60 and 210.
Factors of 75 are 1, 3, 5, 15, 25 and 75.
Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 30 and 60.
Factors of 210 are 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105 and 210.
Thus, common factors of 75, 60 and 210 are 1, 3, 5 and 15.
Example 2: Find the common multiples of 3, 4 and 9.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, ....
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48,...
Multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81, ...
Clearly, common multiples of 3, 4 and 9 are 36, 72, 108,...
Prime Factorization
When a number is expressed as a product of prime numbers, factorization is called prime factorization.
Prime factorization is a way of expressing a number as a product of its prime factors.
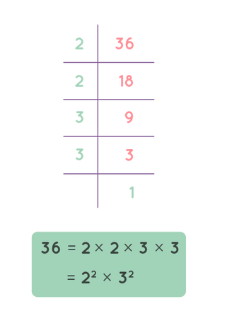
Example: Prime factorization of 36 is 2×2×3×3.
There are two methods to find the prime factors of a number:
1. Prime factorization using a factor tree
Let us understand prime factorization using the factor tree method:
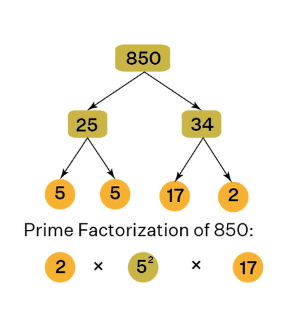
Prime Factorization of 850
- Start with 850 at the top of the tree.
- Divide 850 into factors: 850 = 25 × 34.
- Factorize each composite number:
- 25 = 5 × 5
- 34 = 17 × 2
- Write down the prime factors: 850 = 2 × 5 × 5 × 17
- Prime Factorization: 2 × 5² × 17
2. Repeated Division Method
Let us understand repeated division method:
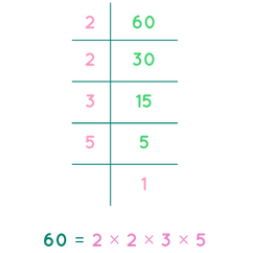
Prime Factorization of 60
- Divide by the smallest prime:
60 ÷ 2 = 30 - Continue dividing the quotient by the smallest prime:
30 ÷ 2 = 15
15 ÷ 3 = 5
5 ÷ 5 = 1 - List all the prime factors:
Prime factorization of 60 = 2 × 2 × 3 × 5
 Q: Find the prime factorization of 2520.
Q: Find the prime factorization of 2520.
Ans: 2520 = 2 × 1260
= 2 × 2 × 630
= 2 × 2 × 2 × 315
= 2 × 2 × 2 × 3 × 105
= 2 × 2 × 2 × 3 × 3 × 35
= 2 × 2 × 2 × 3 × 3 × 5 × 7
Highest Common Factor
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors. It is also known as the Greatest Common Divisor (GCD).
HCF by Prime Factorization Method
Take an example of finding the highest common factor of 144, 104 and 160.
Now let us write the prime factors of 144, 104 and 160.
144 = 2 × 2 × 2 × 2 × 3 × 3
104 = 2 × 2 × 2 × 13
160 = 2 × 2 × 2 × 2 × 2 × 5
The common factors of 144, 104 and 160 are 2 × 2 × 2 = 8
Therefore, HCF (144, 104, 160) = 8
HCF by Division Method
Steps to find the HCF of any given numbers;
1) Larger number/ Smaller Number
2) The divisor of the above step / Remainder
3) The divisor of step 2 / remainder. Keep doing this step till R = 0(Zero).
4) The last step’s divisor will be HCF.
Example 1: Find the HCF of 50 and 75 by the prime factorization method.
- The prime factors of 50 = 2 × 5 × 5 or 2 × 52
- The prime factors of 75 = 3 × 5 × 5 or 3 × 52
The common factors of 50 and 75 are 52 or 5 × 5. Thus, HCF of (50, 75) = 25.
Example 2: Find the HCF of 20 and 12 by the prime factorization method.
To find HCF of 20 and 12, write each number as a product of prime factors.
20 = 2 × 2 × 5 = 22 × 5
12 = 2 × 2 × 3 = 22 × 3Now, Multiply all the common prime factors with the lowest degree. Here we have only 2 as a common prime factor with the lowest power of 2.
HCF of 20 and 12 = 22 = 4
Lowest Common Multiple
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
LCM by Prime Factorization Method
To calculate the LCM of two numbers 60 and 45. Out of other ways, one way to find the LCM of given numbers is as below:
List the prime factors of each number first.
60 = 2 × 2 x 3 × 5
45 = 3 × 3 × 5
Then multiply each factor the most number of times it occurs in any number.
If the same multiple occurs more than once in both the given numbers, then multiply the factor by the most number of times it occurs.
The occurrence of Numbers in the above example:
2: two times
3: two times
5: one time
LCM = 2 × 2 x 3 × 3 × 5 = 180
LCM by Division Method
Let us see with the same example, which we used to find the LCM using prime factorization.
Solve LCM of (60,45) by division method.
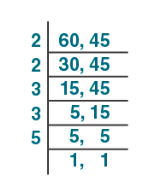
Therefore, LCM of 60 and 45 = 2 × 2 x 3 × 3 × 5 = 180
Example 1: Let us find the LCM of 160 and 90 using prime factorization.
- Step 1: The prime factors of 160 = 2 × 2 × 2 × 2 × 2 × 5. After writing this in the exponent form, we get 25 × 5 and 90 = 2 × 3 × 3 × 5 or 2 × 32 × 5.
- Step 2: Now, if we pick the factors with the highest power, we get 25, 32, and 5. The product of all these prime factors = 25 × 32 × 5 = 1440.
Therefore, LCM of 160 and 90 = 1440.
Example 2: Find the LCM of 20 and 12 by prime factorization method.
Step 1: To find LCM of 20 and 12, write each number as a product of prime factors.
20= 2 × 2× 5
12= 2 × 2 × 3Step 2: Multiply all the prime factors with the highest degree.Here we have 2 with highest power 2 and other prime factors 3 and 5. Multiply all these to get LCM.
LCM of 20 and 12 = 2 × 2 × 3 × 5 = 22 × 3 × 5 = 60
Some Problems on HCF and LCM
Q1: Two tankers contain 850 litres and 680 litres of kerosene oil respectively. Find the maximum capacity of a container which can measure the kerosene oil of both the tankers when used an exact number of times.
Ans:
Given, Two tankers of kerosene oil is 850 litres & 680 litres
We need to find, Maximum measuring capacity of container to measure both tankers
Since measuring capacity = HCF of 850 & 680
We will find HCF
Maximum measuring capacity = HCF of 850 & 680

HCF of 680 & 850
Hence, 680 = 2 × 2 × 2 × 5 × 17
850 = 2 × 5 × 5 × 17
∴ HCF = 2 × 5 × 17 = 170
So, Maximum measuring capacity = 170 litres
To fill 850 litres, we measure 5 times (170 X 5 = 850)
To fill 680 litres, we measure 4 times (170 X 4 = 680)
Q2: In a morning walk three persons step off together, their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that he can cover the distance in complete steps?
Ans:
Given: In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm.
To Find: minimum distance each should walk so that all can cover the same distance in complete steps.
The distance covered by each of them is required to be same as well as minimum. The required distance each should walk would be the L.C.M of the measures of their steps i.e. 80 cm, 85 cm, and 90 cm,
So we have to find the L.C.M of 80 cm, 85 cm, and 90 cm.
80 = 24 x 5
85 = 17 x 5
90 = 2 x 32x 5
L.C.M of 80, 85 and 90 = 24 x 32 x 5 x 17 = 12240 cm
Hence minimum 12240 cm distance each should walk so that all can cover the same distance in complete steps.
Q3: The sum of the two numbers is 216 and HCF is 27. Find the numbers.
Ans: Let the numbers are 27a and 27b.
27a + 27 b = 216
a + b = 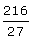 = 8
= 8
Co-primes with sum 8 are (1,7) and (3,5)
Required numbers are (27 x 1 ), (27 x 7) or (27 x 3 ), (27 x 5)
i.e. (27,189) or (81 x 135)
Q4: Write all the numbers less than 100 which are common multiples of 3 and 4.
Ans: To find the common multiples of 3 and 4 less than 100, we need to find numbers that are divisible by both 3 and 4. These are numbers that are multiples of the least common multiple (LCM) of 3 and 4, which is 12. Here are the common multiples of 3 and 4 less than 100:
12, 24, 36, 48, 60, 72, 84, 96
|
30 videos|120 docs|59 tests
|
FAQs on Playing with Numbers Class 6 Notes Maths
| 1. What are factors and multiples? |  |
| 2. How do you find the prime factors of a number? |  |
| 3. What is the difference between HCF and LCM? |  |
| 4. How can you test for the divisibility of numbers? |  |
| 5. Can you explain the concept of prime and composite numbers? |  |






















