Points to Remember: Algebraic Expressions & Identities | Mathematics (Maths) Class 8 PDF Download
Algebraic Expression
Any mathematical expression which consists of numbers, variables and operations are called Algebraic Expression.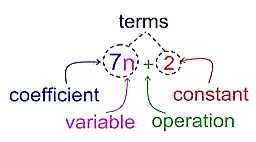
- Terms: Every expression is separated by an operation which is called Terms. Like 7n and 2 are the two terms in the above figure.
- Factors: Every term is formed by the product of the factors.7n is the product of 7 and n which are the factors of 7n.
- Coefficient: The number placed before the variable or the numerical factor of the term is called Coefficient of that variable.7 is the numerical factor of 7n so 7 is coefficient here.
- Variable: Any letter like x, y etc. are called Variables. The variable in the above figure is n.
- Operations: Addition, subtraction etc. are the operations which separate each term.
- 6Constant: The number without any variable is constant. 2 is constant here.
Number Line and an Expression
An expression can be represented on the number line.
Example1: How to represent x + 5 and x – 5 on the number line?
Sol: First, mark the distance x and then x + 5 will be 5 unit to the right of x.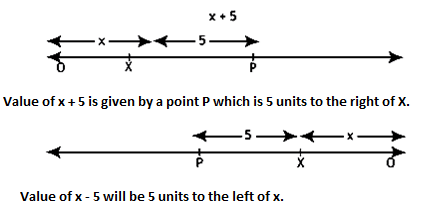
In the case of x – 5 we will start from the right and move towards the negative side. x – 5 will be 5 units to the left of x.
Monomials, Binomials and Polynomials
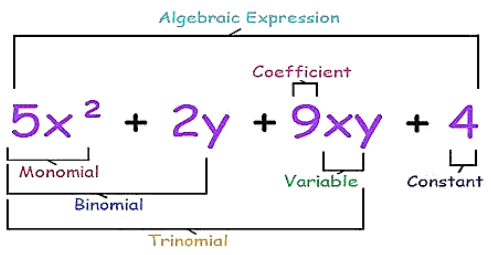
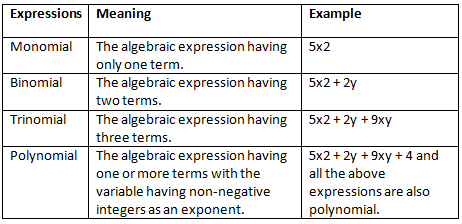
Like and Unlike Terms
Terms having the same variable are called Like Terms.
Examples of Like Terms
- 2x and -9x
- 24xy and 5yx
- 6x2 and 12x2
The terms having different variable are called, Unlike Terms.
Examples of Unlike Terms
- 2x and - 9y
- 24xy and 5pq
- 6x2 and 12y2
Addition and Subtraction of Algebraic Expressions
Steps to add or Subtract Algebraic Expression
- First of all, we have to write the algebraic expressions in different rows in such a way that the like terms come in the same column.
- Add them as we add other numbers.
- If any term of the same variable is not there in another expression then write is as it is in the solution.
Example: Add 15p2 – 4p + 5 and 9p – 11
Sol: Write down the expressions in separate rows with like terms in the same column and add.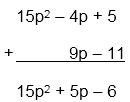
Example: Subtract 5a2 – 4b2 + 6b – 3 from 7a2 – 4ab + 8b2 + 5a – 3b.
Sol: For subtraction also write the expressions in different rows. But to subtract we have to change their signs from negative to positive and vice versa.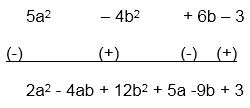
Multiplication of Algebraic Expressions
While multiplying we need to take care of some points about the multiplication of like and unlike terms.
1. Multiplication of Like Terms
- The coefficients will get multiplied.
- The power will not get multiplied but the resultant variable will be the addition of the individual powers.
Example
- The product of 4x and 3x will be 12x2.
- The product of 5x, 3x and 4x will be 60x3.
2. Multiplication of Unlike Terms
- The coefficients will get multiplied.
- The power will remain the same if the variable is different.
- If some of the variables are the same then their powers will be added.
Example
- The product of 2p and 3q will be 6pq
- The product of 2x2y, 3x and 9 will be 54x3y
Multiplying a Monomial by a Monomial
1. Multiplying Two Monomials
While multiplying two polynomials the resultant variable will come by
- The coefficient of product = Coefficient of the first monomial × Coefficient of the second monomial
- The algebraic factor of product = Algebraic factor of the first monomial × Algebraic factor of the second monomial.
Example
25y × 3xy = 125xy2
2. Multiplying Three or More Monomials
While multiplying three or more monomial the criterion will remain the same.
Example
4xy × 5x2y2 × 6x3y3 = (4xy × 5x2y2) × 6x3y3
= 20x3y3 × 6x3y3
= 120x3y3 × x3y3
= 120 (x3 × x3) × (y3 × y3)
= 120x6 × y6
= 120x6y6
We can do it in other way also
4xy × 5x2y2 × 6x3 y3
= (4 × 5 × 6) × (x × x2 × x3) × (y × y2 × y3)
= 120 x6y6
Multiplying a Monomial by a Polynomial
1. Multiplying a Monomial by a Binomial
To multiply a monomial with a binomial we have to multiply the monomial with each term of the binomial.
Example
- Multiplication of 8 and (x + y) will be (8x + 8y).
- Multiplication of 3x and (4y + 7) will be (12xy + 21x).
- Multiplication of 7x3 and (2x4 + y4) will be (14x7+ 7x3y4).
2. Multiplication of Monomial by a trinomial
This is also the same as above.
Example
- Multiplication of 8 and (x + y + z) will be (8x + 8y + 8z).
- Multiplication of 4x and (2x + y + z) will be (8x2 + 4xy + 4xz).
- Multiplication of 7x3 and (2x4+ y4+ 2) will be (14x7 + 7x3y4 + 14x3).
Multiplying a Polynomial by a Polynomial
1. Multiplying a Binomial by a Binomial
We use the distributive law of multiplication in this case. Multiply each term of a binomial with every term of another binomial. After multiplying the polynomials we have to look for the like terms and combine them.
Example: Simplify (3a + 4b) × (2a + 3b)
Sol:
(3a + 4b) × (2a + 3b)
= 3a × (2a + 3b) + 4b × (2a + 3b) [distributive law]
= (3a × 2a) + (3a × 3b) + (4b × 2a) + (4b × 3b)
= 6 a2 + 9ab + 8ba + 12b2
= 6 a2 + 17ab + 12b2 [Since ba = ab]
2. Multiplying a Binomial by a Trinomial
In this also we have to multiply each term of the binomial with every term of trinomial.
Example: Simplify (p + q) (2p – 3q + r) – (2p – 3q) r.
Sol:
We have a binomial (p + q) and one trinomial (2p – 3q + r)
(p + q) (2p – 3q + r)
= p(2p – 3q + r) + q (2p – 3q + r)
= 2p2 – 3pq + pr + 2pq – 3q2 + qr
= 2p2 – pq – 3q2 + qr + pr (–3pq and 2pq are like terms)
(2p – 3q) r = 2pr – 3qr
Therefore,
(p + q) (2p – 3q + r) – (2p – 3q) r
= 2p2 – pq – 3q2 + qr + pr – (2pr – 3qr)
= 2p2 – pq – 3q2 + qr + pr – 2pr + 3qr
= 2p2 – pq – 3q2 + (qr + 3qr) + (pr – 2pr)
= 2p2 – 3q2 – pq + 4qr – pr
Identities
An identity is an equality which is true for every value of the variable but an equation is true for only some of the values of the variables.
So an equation is not an identity.
Like, x2 = 1, is valid if x is 1 but is not true if x is 2.so it is an equation but not an identity.
Some of the Standard Identities
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 – 2ab + b2
a2 – b2 = (a + b) (a - b)
(x + a) (x + b) = x2 + (a + b)x + ab
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
These identities are useful in carrying out squares and products of algebraic expressions. They give alternative methods to calculate products of numbers and so on.
Applying Identities
Example
(4x – 3y)2
= (4x)2 – 2(4x) (3y) + (3y)2
= 16x2 – 24xy + 9y2
Example: Use the Identity (x + a) (x + b) = x2 + (a + b) x + ab to find the value of 501 × 502
Sol:
501 × 502
= (500 + 1) × (500 + 2)
= 5002 + (1 + 2) × 500 + 1 × 2
= 250000 + 1500 + 2
= 251502
|
79 videos|409 docs|31 tests
|
FAQs on Points to Remember: Algebraic Expressions & Identities - Mathematics (Maths) Class 8
| 1. How do you add algebraic expressions with like terms? |  |
| 2. Can you subtract algebraic expressions with unlike terms? |  |
| 3. How do you simplify algebraic expressions before performing addition or subtraction? |  |
| 4. What is the difference between adding and subtracting algebraic expressions? |  |
| 5. Can you add or subtract algebraic expressions with different variables? |  |


















