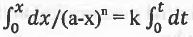Points to be Remembered
1. Determination of Order from Rate Constant: The order of a reaction can be determined from the unit of the rate constant.
We know that: dC/dt = kCn .......... (1)
where, C = Concentration of reactant, k = rate constant and n = order of the reaction
or, dC/Cn = k.dt or, C(1-n).t-1 = k ............(2)
For, zero order reaction i.e. n = 0, the unit of rate constant will be : C(1-0).t-1 = M .sec-1
For first order reaction i.e. n = 1, the unit of the rate constant will be : C(1-1).t-1 = sec-1 For second order reaction i.e. n = 2, the unit of the rate constant will be : C(1-2).t-1 = M-1.sec-1
For third order reaction i.e. n = 3, the unit of the rate constant will be : C(1-3).t-1 = M-2.sec-1
2. Factors Affecting the Rate of a Reaction: The following factors influences the rate of a reaction.
I. Concentration of Reactant: Reactant concentration has a vital role on the rate of a chemical reaction. Greater is the reactant concentration in a chemical reaction, higher will be the no. of molecules available per unit volume for collision. Hence, greater will be the no. of collisions. Hence, the rate of the reaction will be increased.
II. Nature of Reactants and Products: Rate of a reaction is largely dependent on the nature of reactants and products. Depending upon the bonds breaking and formation of reactants and products, some reaction occurs at a faster rate while some occurs at a slower rate.
III. Temperature: Temperature greatly influenced the rate of a chemical reaction. Higher is the temperature, greater will be the collisions resulting the reaction to occur at a faster rate. It is observed that the reaction rate become doubles per 10° rise in temperature.
IV. Surface Area of Solid Reactants: For a heterogeneous reaction, greater is the surface area of solid reactant, more no. of molecules will get attach to the surface of the reactant. Hence, greater no. of collision will occur. Hence, the reaction rate will be increased.
V. Effect of Catalyst: Rate of a chemical reaction is highly affected by the catalyst. Catalyst always provides an alternative pathway which involves lower activation energy for the reaction to occur. Hence, the reaction rate will be increased.
3. Difference Between Order and Molecularity:
1. Order may be positive, negative, zero or, even fractional but molecularity must be positive integer.
2. Order may be affected by the temperature, pressure, concentration of reactants but molecularity remains unaffected by these factors.
3. Order is an experimentally determined quantity while molecularity is a theoretical concept.
4. Zero Order Reaction:
A. Integrated Rate Law: Let us consider the following zero order reaction : Let a M be the initial concentration of the reactant. After a certain time t, if x M be the concentration of product then (a-x) M be the concentration of reactant after time t.
A ---> pdt
t = 0 a 0
t = t (a-x) x
Rate = -d(a-x)/dt = k(a-x)° or, dx/dt = k
or, dx = k.dt
on integration, we have:
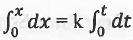
or, x = kt
This is the integrated rate equation for a zero order reaction.
B. Half-life of Zero Order Reaction: The integrated rate equation for a zero order reaction is: x = kt ..........(3)
When t = t1/2, x = a/2.
Putting these values into the equation (3), we have:
a/2 = kt1/2 or, t1/2 = a/2k or, t1/2 ∝ a
Hence, the half-life of a zero order reaction is directly proportional to the first power of the initial concentration of reactant.
C. Completion of Zero Order Reaction: The integrated rate equation for a zero order reaction is:
x = kt or, (a-x) = a-kt ....... (4)
When t = tcom, (a-x) = 0. Putting these values into the equation (4), we have:
0 = a-ktcom or, a ktcom or, tcom = a/k
Hence, a zero order reaction goes to completion.
D. Graphical Plots:
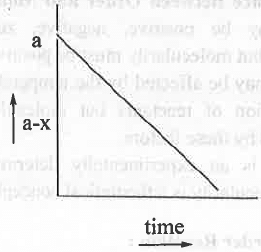
I. [Reactant] vs. t: The integrated rate equation for a zero order reaction is:
x = kt or, (a-x) = a-kt ....... (5)
Hence, a plot of (a-x) vs. t will be a straight line with negative slope = k and the Y-axis intercept a.
 II. [Product]vs. t: The integrated rate equation for a zero order reaction is:
II. [Product]vs. t: The integrated rate equation for a zero order reaction is:
x = kt ....... (5)
Hence, a plot of a vs. t will be a straight line passing through the origin with positive slope = k.
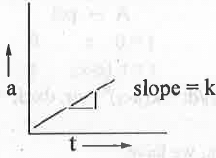
E. Characteristics of a Zero Order Reaction: Some important characteristics of a zero order reaction are:
I. The unit of the rate constant of a zero order reaction is M.sec-1.
II. The integrated rate equation of a zero order reaction is: x = kt.
III. A zero order reaction goes to completion in a finite time.
IV. The half-life of a zero order reaction is dependent on the initial concentration of reactant.
V. A plot of [R] vs. t will be a straight line with negative slope k and Y-axis intercept a while a plot of [P] vs. t will be a straight line passing through the origin with positive slope k.
5. First Order Reaction:
A. Integrated Rate Law: Let us consider the following first order reaction : Let a M be the initial concentration of the reactant. After a certain time t, if x M be the concentration of product then (a-x) M be the concentration of reactant after time t.
A ----> pdt
t = 0 a 0
t = t (a-x) x
Rate = -d(a-x)/dt = k(a-x)1 or, dx/dt = k(a-x)
or, dx/(a-x) = k.dt
on integration, we have:
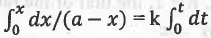
or, ln[a/(a-x)] = kt
This is the integrated rate equation for a first order reaction.
B. Half-life of First Order Reaction: The integrated rate equation for a first order reaction is:
ln[a/(a-x)] = kt ......... (6)
When t = t1/2 , x = a/2.
Putting these values into the equation (6), we have:
ln2 = kt1/2 or, t1/2 = 0.693/k or, t1/2 ∝ a°
Hence, the half-life of a first order reaction is independent on the initial concentration of reactant.
C. Completion of First Order Reaction: The integrated rate equation for a first order reaction is:
ln[a/(a-x)] = kt or, ln[(a-x)/a] = -kt or, [(a-x)/a] = e-kt or, (a-x) = a.e-kt ....... (7)
When t = tcom, (a-x) = 0.
Putting these values into the equation (7), we have:
0 = ae-ktcom or, tcom = ∞
Hence, a first order reaction never goes to completion.
D. Graphical Plots:
I. ln[a/(a-x)] vs. t: The integrated rate equation for a first order reaction is:
ln[a/(a-x)] = kt ......... (8)
Hence, a plot of ln[a/(a-x)] vs. t will be a straight line passing through the origin with positive slope = k.
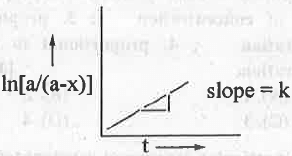 E. Characteristics of a First Order Reaction: Some important characteristics of a first order reaction are:
E. Characteristics of a First Order Reaction: Some important characteristics of a first order reaction are:
1. The unit of the rate constant of a first order reaction is sec-1.
2. The integrated rate equation of a first order reaction is: ln[a/(a-x)] = kt.
3. A first order reaction never goes to completion.
4. The half-life of a first order reaction is independent on the initial concentration of reactant.
5. A plot of ln[a/(a-x)] vs. t will be a straight line passing through the origin with positive slope k.
6. n-th Order Reaction:
A. Integrated Rate Law: Let us consider the following n-th order reaction : Let a M be the initial concentration of the reactant. After a certain time t, if x M be the concentration of product then (a-x) M be the concentration of reactant after time t.
A -> pdt
t = 0 a 0
t = t (a-x) x
Rate = -d(a-x)/dt = k(a-x)n or, dx/dt = k(a-x)n or, dx/(a-x)n = k.dt
on integration, we have:
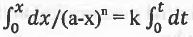
or, 1/(n - 1)[(a-x)1-n - a1-n] = kt
B. Half-life of n-th Order Reaction: The integrated rate equation for n-th order reaction is:
1/(n - 1) [(a - x)1-n - a1-n] = kt ........ (9)
When t = t1/2, x = a/2.
Putting these values into the equation (9), we have:
1/(n-1)[(a-a/2)1-n - a1-n] = kt1/2 or, 1/(n-1)[(a/2)1-n - a1/n] = kt1/2
or, 1/(n-1).a1-n[2n-1 -1] = kt1/2
or, t1/2 ∝ a1-n
C. Limitation: This rate law is not applicable for first order reaction.
7. Pseudo First Order Reaction: Let us consider the hydrolysis of sucrose in acidic medium.

Rate = k[Sucrose][H2O][H+]
As H+ acts as catalyst, it will not appear in the rate equation.
Hence, rate = k'[Sucrose][H2O]
Here, water is present in excess. Hence, it will not affect the rate of the reaction.
Hence, rate = k''[Sucrose] ; k" = k'[H20 ]
At first sight, it is seemed the reaction is first order with respect to sucrose and the reaction is also first order with respect to water, But, as water is present in excess, rate will be independent on the concentration of water. That's why the overall order of the reaction will be first. Hence, it is called pseudo first order reaction.
8. Some Important Formulas:
1. C(1-n).t-1 = k - used to find out the order of a reaction from the unit of rate constant.
2. The integrated rate equation for a first order reaction is: ln[a/(a-x)] = kt
3. The half-life for a first order reaction is: t1/2 = 0.693/k
4. The integrated rate equation for n-th order reaction is: 1/(n - 1)[(a- x)1-n - a1-n] = kt
5. The half-life for a n-th order reaction is: t1/2 = 1/(n-1)k.a1-n[2n-1-1]
6. The Arrhenius equation is: k = A.e'[Ea/RT]
7. ln(k2/k1) = Ea/R.[1/T1 - 1/T2] - used to determine the activation energy of a reaction having two different rate constants at two different temperatures.
8. Rate of the homogeneous catalytic reaction: r = d[P]/dt
9. The turnover frequency (TOF) = r/Q = Rate/[Catalyst]
10. The order of a reaction is related to half-life time and concentrations of reactants through the following equation: n = 1 + log[(t1/22/t1/2]1/log(a01/a02)].
11. Lineweaver-Burk equation is : 1/v = (l/vmax) + (Km/ vmax).(1/[S]0) ......... (1)
12. Turnover no. = Vmax/[E]o
13. Catalytic efficiency = kcat/KM
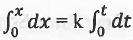
 II. [Product]vs. t: The integrated rate equation for a zero order reaction is:
II. [Product]vs. t: The integrated rate equation for a zero order reaction is: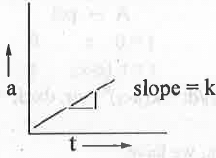
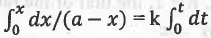
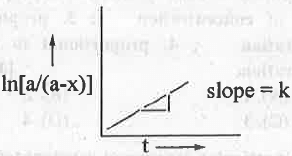 E. Characteristics of a First Order Reaction: Some important characteristics of a first order reaction are:
E. Characteristics of a First Order Reaction: Some important characteristics of a first order reaction are: