Polygons: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Polygons
Polygon is nothing but a closed figure(end to end connected) made up of more than 2 line segments on a 2-dimensional plane. The word Polygon made up of 2 words first Poly means “many” and gons means “sides”. Polygon means nothing but a shape having many sides. Or in other words, the polygon is created by using straight-line segments that are end to end connected with each other, and these line segments are known as sides of the polygon and the point is known as the vertex of the polygon. If a shape does not contain sides and angles then they are not a polygon-like circle. Some of the polygons are:
Properties of Polygon
- The measure of each exterior angle of an n-sided regular polygon will be 360°/n.
- The measure of each interior angle of n-sided regular polygon will be [(n – 2) × 180°]/n.
- The number of triangles formed by joining the diagonals from one corner of a polygon will be n – 2.
- The number of diagonals in a polygon with n sides will be n(n – 3)/2.
- The sum of all the interior angles of an n-sided polygon will be (n – 2) × 180°.
Terminology
1. Diagonals: A line segment joining two non-consecutive vertices of a polygon is known as a diagonal. For example, in the given figure, AC and BD are the two diagonals of the ABCD square.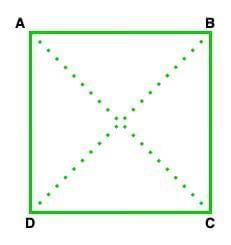
2. Adjacent Sides: In a polygon, if two sides share a common vertex then such type of sides is known as adjacent sides. For example, in the above figure, AD and DC are the adjacent sides.
3. Adjacent Vertex: In a polygon, if two endpoints or vertex of the same side, then such type of vertex is known as the adjacent vertex. For example, in the above figure vertex, A and B are the adjacent vertex of side AB.
Types of polygons
There are 4 types of Polygon:
- Regular Polygon: If all the sides and interior angles of the polygon are equal or if a polygon is equiangular and equilateral, then the polygon will be known as a regular polygon. Example square, rhombus, equilateral triangle, etc.

- Irregular Polygon: If all the sides and the interior angles of the polygon are of different measure, then the polygon will be known as an irregular polygon. Example scalene triangle, rectangle, and kite, etc.

- Convex Polygon: If all the interior angles of a polygon are strictly less than 180° or if a line segment between two points on the boundary does not go outside the polygon, then the polygon will be known as a convex polygon.

- Concave Polygon: If one or more interior angles of a polygon are more than 180° degrees or a polygon contains at least one reflex interior angle, then the polygon will be known as a concave polygon. This polygon can have at least four sides.
Angles of Polygon
There are two types of angles in polygons:
- Interior Angle: It is an angle from inside a shape, or we can say that angle form inside a polygon and the sum of the interior angles of the polygon is
Interior angle sum = (n – 2) x 180, Here, n is the total number of sides of a polygon
or
Interior Angle = 180° – Exterior Angle,
or in radian,
Interior angle sum= = (n – 2)π radian.
For example:
- Exterior Angle: It is an angle form by a side and an extension of an adjacent side and the sum of exterior angles of a polygon is equal to 360o. The sum of the exterior angles of the polygon is
Exterior Angle = 180° – Interior Angle
If a polygon has n sides then
The sum of all exterior angle = n x 180° – sum of all interior angle
Important points
- In every polygon, the addition of exterior angles will be always 360°.
- For a regular polygon, the size of each exterior angle = 360° ÷ number of sides.
- For a regular polygon, the number of sides = 360° ÷ size of the exterior angle.
For example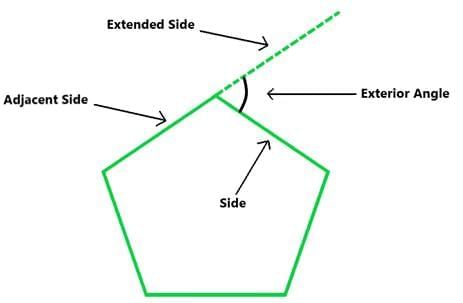
Classification of Polygons
Polygons are classified based on their number of sides or vertices they have. So, some of the polygons are:
Polygon | No. of sides | No. of Diagonal | No. of vertices | Interior Angle |
Triangle | 3 | 0 | 3 | 60 |
Quadrilateral | 4 | 2 | 4 | 90 |
Pentagon | 5 | 5 | 5 | 108 |
Hexagon | 6 | 9 | 6 | 120 |
Heptagon | 7 | 14 | 7 | 128.571 |
Octagon | 8 | 20 | 8 | 135 |
Nonagon | 9 | 27 | 9 | 140 |
Decagon | 10 | 35 | 10 | 144 |
Hendecagon | 11 | 44 | 11 | 147.273 |
Dodecagon | 12 | 54 | 12 | 150 |
Triskaidecagon | 13 | 65 | 13 | 158.308 |
Tetrakaidecagon | 14 | 77 | 14 | 154.286 |
Pentadecagon | 15 | 90 | 15 | 156 |
Triangles(3-gon)
A triangle is a polygon, it is formed with the help of three-line segments intersecting each other, so a triangle has 3 vertices, 3 edges, and 3 angles. The triangles are classified into different types, based on the sides and angles. Some properties of the triangle:
Some properties of the triangle:
- Area of Triangle: 1/2× base × height
- In a triangle, the sum of all the interior angles of a triangle is 180o.
- The side opposite to the largest angle is the largest side of the triangle.
- The perimeter of a triangle is equal to the sum of lengths of all three sides of the triangle.
Based on sides
- Equilateral triangle: If a triangle having all sides equal and angles of equal measure then such types of triangles are known as equilateral triangle.
- Isosceles triangle: If any triangle having any 2 sides equal and angles opposite to the equal sides are equal, then such types of triangles are known as isosceles triangles.
- Scalene triangle: If a triangle having all the 3 sides unequal, then such types of triangles are known as a scalene triangle.

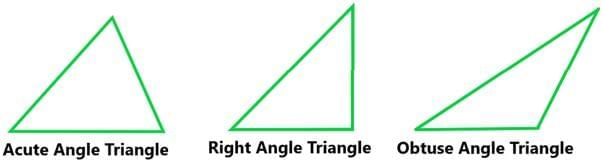
Based on angle
- Acute Angled Triangle: A triangle having each angle less than 90°, then such type of triangle is known as acute-angle triangle.
- Right Angled Triangle: If any one of the three angles of triangle equal to 90° then such type of triangle is known as right-angle triangle.
- Obtuse Angled Triangle: If any one angle of a triangle is greater than 90°, then such type of triangle is known as obtuse-angle triangle.
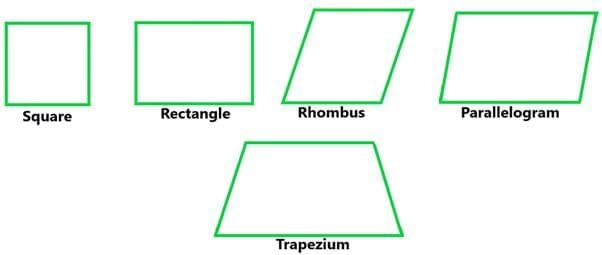
Quadrilaterals (4-gon)
A Quadrilateral is nothing but a polygon having at least 4 sides. A polygon is formed by enclosing four line segments such that they meet at each other at vertices to make 4 or more angles. Example: Square, Rectangle, Parallelogram, Rhombus, Trapezium.
Some properties of a quadrilateral:
- It has four sides.
- It has four vertexes.
- In a quadrilateral, the sum of all the interior angles is 360o.
Sample Problems
Question 1. Find the exterior angle of a regular hexagon?
Solution:
As we know that, hexagon has 6 sides therefore
Exterior Angle = 360o / n = 360o / 6
Exterior Angle = 60o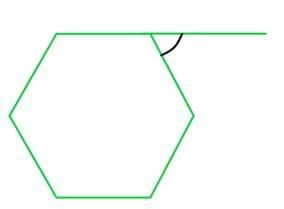
Question 2. Find the interior angle of a regular pentagon?
Solution:
As we know that pentagon has 5 sides, therefore
Exterior Angle = 360o / 5 = 72o
Interior Angle = 180o – 72o = 108o
Question 3. Find each interior angle of a regular decagon.
Solution:
As we know that, decagon has ten sides.
Using angle sum formula,
As we know that,
S = (n − 2) × 180°
Here, n = 10
Therefore,
Sum of angles of decagon = (10 − 2) × 180°
= 8 × 180° = 1440°
As we know that all the interior angles are equal of a regular decagon,
Therefore, the measure of each interior angle of regular decagon = sum of interior angles / number of sides
Interior angle = 1440 / 10 = 144°
Hence, Sum of Interior Angle of decagon is 1440° and each interior angle is of 144°.
Question 4. Find the value of x in the given figure:
Solution:
As we know that the sum of angles os a quadrilateral = 360o
so, 55o + 124o + 70o + x = 360o
249o + x = 360o
x = 111o
Question 5. Find the value of x in the given figure: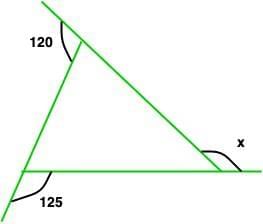
Solution:
As we know that the sum of exterior angles = 360o
So, 120o + 125 + x = 360o
245o + x = 360o
x = 360o – 245o
x = 115o
|
22 videos|133 docs|11 tests
|
FAQs on Polygons: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is a polygon, and how is it classified? |  |
| 2. What are the properties of quadrilaterals? |  |
| 3. How do you calculate the area of a quadrilateral? |  |
| 4. What distinguishes a regular quadrilateral from an irregular quadrilateral? |  |
| 5. Can you name some real-life examples of quadrilaterals? |  |





















