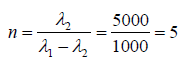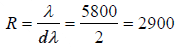Position of Maxima & Minima | Oscillations, Waves & Optics - Physics PDF Download
Condition for Principle Maxima
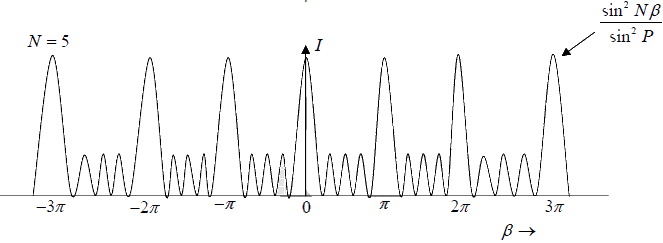
When the value of N is very large, one obtains intense maxima when sinβ = 0 . This condition arises when
β = ±nπ where n = 0,1,2,3.....
so sin Nβ = 0
Thus 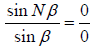 (indeterminate form), thus
(indeterminate form), thus
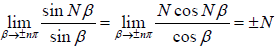
Thus intensity
Such maxima are most intense and are known as principal maxima. Physically, at these maxima the fields produced by each of the slits are in phase, and therefore, they add and
the resultant field is N times the field produced by each of the slits.
They are obtained in the direction given by β = ±nπ
(b + e)sinθ = ±nλ where n = 0,1,2...
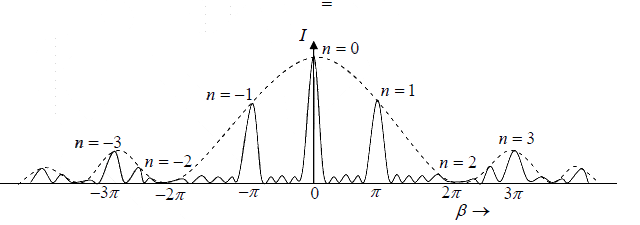
This is the condition of maxima where for n = 0 , we get the zero order principle maximum. For n = ±1,+2 + 3..... we obtain the first, second, third- order principal maxima respectively. The ± sign show that there are two principal maxima for each order
lying on either side of the zero order maximum.
Condition for Minima
The intensity is zero when sin Nβ = 0 but sinβ ≠ 0 then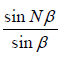 = 0
= 0
( sinβ = 0 gives maximum intensity). Thus minimum are obtained in the directions given by
sin Nβ = 0 ⇒ Nβ = ±m′π ⇒ 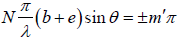
Thus the condition of minimum intensity is
N (b + e)sinθ = ±m′λ
where m′ takes all integral values except 0, N,2N.... nN . Because these value of m′ makes sinβ = 0 , which gives principal maxima.
It is clear from above that m′ = 0 gives the principal maximum and m′ = 1, 2,3.. (N −1) give minima and then m′ = N give again a principal maximum. Thus there are (N −1) minima between two consecutive principal maxima.
Condition for Secondary Maxima
As there are (N −1)minima between two consecutive principal maxima, there must be (N − 2) other maxima between two principal maxima these are called secondary maxima.
Their positions are obtained by differentiating the formula of intensity I with respect to
β and equating it equal to zero. Thus
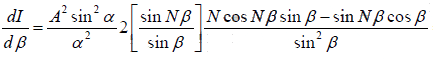 = 0
= 0
N cos nβ sinβ = sin Nβ cosβ ⇒ tan Nβ = N tanβ ----(1)
To find the value of 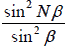 under the condition (1), we make use of the triangle shown
under the condition (1), we make use of the triangle shown
in figure (1), this gives
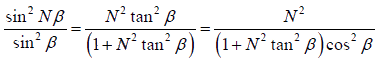
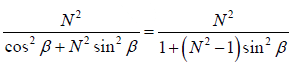
This gives 
This shows that the intensity of the secondary maxima is proportional to , where the intensity of the principal maxima is proportional to N2 so,
, where the intensity of the principal maxima is proportional to N2 so,
Hence greater the value of N , the weaker are secondary maxima. In an actual grating, N
is very large. Hence these secondary maxima are not visible in the grating spectrum.
Condition for absent spectra
A particular principal maximum may be absent if it corresponds to the angle which also determines the minimum of the single-slit diffraction pattern.
Principal maxima in the grating spectrum are obtained in the direction given by
(b + e)sinθ = nλ -----(1)
where n is the order of maximum.
The minima in a single slits pattern are obtained in the direction given by
bsinθ = mλ m =1,2,3... -----(2)
If both (1) and (2) are satisfied simultaneously, a particular maximum of order n will be
missing in the grating spectrum.
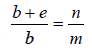
this is the condition for the spectrum of the order n to be absent.
If e = b then n = 2m = 2,4,6... i.e. 2nd, 4th, 6th, order spectra will be absent
If e = 2b then n = 3m = 3,6,9... i.e. 3rd, 6th, 9th…… order spectra will be absent
Example 4: Monochromatic light beam a helium-neon laser (λ = 632.8 nm) is incident normally on a diffraction grating containing 6000 grooves per centimeter. Find the angles at which the 1st and 2nd order maxima are observed. What if we look for the 3rd order maxima? Do we find it?
First we must calculate the slit separation, which is equal to the inverse of the
number of grooves per centimeter.
d = 1/6000cm = 1.667 x 10-4 cm = 1667 nm
For the 1st order maximum (n =1) , we obtain
= 0.3796 ⇒ θ1 = 22.31o
For the 2nd order maximum (n = 2) , we find
= 0.7592 ⇒ θ2 = 49.39o
For 3rd order maximum (n = 3) , we find
= 1.139
because sinθ cannot exceed unity, this does not represent a realistic solution. Hence only zeroth 1st & 2nd order maxima are observed for this situation
Rayleigh Criterion of Resolution and Resolving Power
The resolving power of an optical instrument represents its ability to produce distinctly
separate spectral lines of light having two or more close wavelengths.
Rayleigh’s Criterion of Resolution
Lord Rayleigh proposed the following criterion for resolution which has been universally adopted. “Two spectral lines of equal intensities are just resolved by an optical instrument when the principal maximum of the diffraction pattern due to one falls on the first minimum of the diffraction pattern of the other.
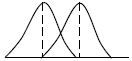
Resolving Power of a Grating
The resolving power of a grating represents its ability to form separate spectral lines for
wavelengths very close together. It is defined by R = λ/Δλ where Δλ is the separation of
the two wavelengths which the grating can just resolve; the smaller the value ofΔλ , larger the resolving power.
Let a parallel beam of light of two wavelengths of λ and λ + dλ be incident normally on the grating. If the nth principal maximum of λ is formed in the direction n θn , we have
(b + e)sinθn = nλ (1)
where (b + e) is the grating element. Let the first minimum adjacent to the
nth maximum be obtained in the direction (θn + dθn )
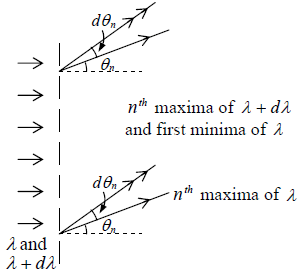
The equation for the minima is
N (b + e)sinθ = m′λ (2)
here θ = θn + dθn
where N is the total number of rulings on the grating and m′ takes all integral values except 0, N,2N,....n N because these values of m′ give 0th ,1st ,2nd ,....nth principal maximum respectively.
Clearly, the first minimum adjacent to the principal maximum in the direction of θ increasing will be obtained for m′ = (nN +1) . Therefore, if this minimum is obtained in
the direction θn + dθn , we have from equation (2)
N (b + e)sin(θn + dθn) = (nN +1)
N (b + e)sin(θn + dθn) = 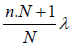 (3)
(3)
By Rayleigh’s criterion, the wavelengths λ and (λ + dλ ) are just resolved by the grating
when the nth maximum of (λ + dλ ) is also obtained in the direction θn + dθn . Then, we
have from equation (1)
(b + e)sin(θn + dθn) = n λ + dλ (4)
Comparing equation (3) and (4), we get
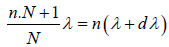
n.Nλ +λ = Nnλ + +Nndλ
λ = Nndλ
λ/dλ = nN
But λ/dλ is the resolving power R of the grating.
Therefore, R = λ/dλ = nN
The above expression may be written as
R = nN = 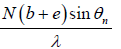
But N (b + e) is the total width of the grating. Hence at a particular angle of diffraction θn, the Resolving Power is directly proportional to the total width of the ruled space on the grating.
Difference between Dispersive Power and Resolving Power
The dispersive power of a diffraction grating gives us an idea of the angular separation between the lines of a spectrum produced by a grating, it is measured by 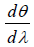 where dθ
where dθ
is the angular separation between two spectral lines whose wavelengths differ by dλ .
The value of Dispersive Power is given by
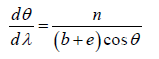
Thus, higher is the order n of the spectrum or closer are the rulings on the grating (i.e. smaller the value of (b + e) greater is the dispersive power.
The resolving power of the grating, on the other hand, expresses the degree of closeness
which the spectral lines can have and yet be distinguished as two. It is measured by λ/dλ,
where dλ is the smallest wavelength λ . The value of Resolving Power is given by
λ/dλ = nN
where, N is the total number of rulings on the grating and n is order of diffraction. Thus
greater is the width of the ruled surface, higher is the resolving power. The higher
resolving power results in sharp maxima.
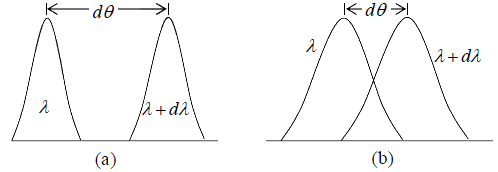
Resolving power is greater in case (a) than case (b).
Example 5: When a gaseous element is raised to a very high temperature, the atoms emit radiation having discrete wavelengths. Tow strong components in the atomic spectrum have wavelengths of 5890 A0 & 5896 A0 .
(a) What resolving power must a grating have if these wavelengths are to be distinguished?
(b) To resolve these lines in the second-order spectrum, how many slits of the grating must be illuminated?
(a) Resolving power is defined as
where λ =
= 5890 + 5896/2 = 5893 A0
Δλ = λ −λ = 5896 − 5890 = 6 A0
∴ R =
= 982 ⇒ R = 982
(b) Resolving power also defined as R = nN where n is the order of spectrum and N is number of slits
N = R/n = 982/2 = 491 slits
Example 6: A beam of light is incident normally on a diffraction grating of width 1 cm. It is found that at 30o, the nth order diffraction maximum for λ1 = 600 Ǻ is super-imposed on the (n+1)th order for λ2 = 500 Ǻ. How many lines per cm does the grating have? Find out whether the first order spectrum from such a grating can be used to resolve the wavelengths λ3 = 5800 Ǻ and λ4 = 5802 Ǻ?
Condition for diffraction maxima is
(b + e)sinθ = nλ
For given two wavelength the maxima condition can be written as
(b + e)sin 30o = nλ1 and (b + e) sin 30o = (n +1)λ2
Taking ration of the two, we get
The grating element is
(b + e) sin 30o = 5×500Α0 ⇒ b + e = 5×10−5cm
Number of grating is
N = Grating width/Grating element = W/(b + e) = 1/5 x 10-5 = 20000
Resolving power of this Grating is
R = λ/dλ = nN
For 1st order spectrum, the resolving power of the given grating is
R = nN = 20000
Whereas to resolve the wavelengths λ3 = 5800 Ǻ and λ4 = 5802 Ǻ the required resolving power is
Resolving power of the given grating (20000) is more than required(2900) . Thus, given grating will resolve the wavelengths λ3 = 5800 A0 and λ4 = 5802 A0.
|
54 videos|22 docs|14 tests
|
FAQs on Position of Maxima & Minima - Oscillations, Waves & Optics - Physics
| 1. What are the conditions for minima in spectra? |  |
| 2. How can secondary maxima be formed in spectra? |  |
| 3. What are the conditions for absent spectra? |  |
| 4. What is the position of maxima and minima in spectra? |  |
| 5. Can you provide some frequently asked questions (FAQs) related to maxima and minima in IIT JAM Physics exam? |  |